物理の交差点:理力记事本(2)
用小栗当封面,是为了纪念小栗在高三支撑着我走下去的无数个晚自习
上文:理力记事本(1):https://zhuanlan.zhihu.com/p/655892408
续·哈密顿力学
量子力学从这里出发
\[\require{newcommand} \def\oiint{{\bigcirc}\kern-11.5pt{\int}\kern-6.5pt{\int}}\]本节大部分from高显
众所周知,薛定谔方程是波动方程,而正是哈密顿雅可比体系中暗含的波动性最终导出了薛定谔方程
在哈密顿量不显含t的情况下,希望S可以分离变量写作
\[S=\Sigma W_i(q^i)-Et\]写作向量形式
\[\vec p=(p_1,...,p_n)=\nabla W\]代入$H=\frac{1}{2m}(p_ip^i)+V=E$(为了方便,考虑度规为I的特殊情况)
\[\partial_i W\partial^iW=2m(E-V)\]粒子在运动演化中始终有dS=0,即
\[dS=|\nabla W|ds-Edt=0\] \[|\nabla W|ds=Edt\] \[\frac{ds}{dt}=\frac{E}{\sqrt{2m(E-V)}}:=u\]回忆一维波函数:$u(x,t)=Asin(wt-\frac{2\pi}{\lambda}x)$,其中相位是$wt-\frac{2\pi}{\lambda}x$,包含了随时间变化的t项和随空间变化的x项,正好对应上文的S=W-Et,W代表空间导致的相移,E代表时间导致的相移。
而ds/dt不仅是物体的真实速度,也可以看作S的相速度u(类似于$\frac{\lambda}{T}=v$)
几何光学是波动光学在短波下的近似,同样经典力学也是也是某种波动的力学(也即量子力学)的近似
先写出一个波函数,并因为S包含空间与时间双重属性,所以把S塞到相位里面去
\[\Psi(t,x)=e^{\frac{i}{\hbar}S(t,x)}=e^{\frac{i}{\hbar}[W(x)-Et]}\]写出波函数通用的方程
\[\frac{\partial^2\Psi}{\partial t^2}=u^2\nabla^2\Psi\]其中的u就是上文中的传播速度,现在把对时间偏导那一项展开(经典的对exp的求导)
\[\frac{\partial\Psi}{\partial t}=-\frac{i}{\hbar}E\Psi\] \[\frac{\partial^2\Psi}{\partial t^2}=-\frac{1}{\hbar^2}E^2\Psi\]从第一个反解出$E\Psi=-\frac{\hbar}{i}\frac{\partial\Psi}{\partial t}$,待会用
代回波函数,u也带进去
\[-\frac{1}{\hbar^2}E^2\Psi=\frac{E^2}{2m(E-V)}\nabla^2\Psi\] \[E\Psi-V\Psi=-\frac{\hbar^2}{2m}\nabla^2\Psi\]E有点傻,用psi对时间的偏导带掉
\[i\hbar\frac{\partial\Psi}{\partial t}-V\Psi=-\frac{\hbar^2}{2m}\nabla^2\Psi\] \[i\hbar\frac{\partial\Psi}{\partial t}=V\Psi-\frac{\hbar^2}{2m}\nabla^2\Psi\]好了,这就是所谓薛定谔方程,看上去就是把作用量S看作相位,丢到波动函数ψ里面,再代入波动方程,得到的东西
通过算符替换的方式快速得到薛定谔方程:首先由
\[H\Psi=\frac{p^2}{2m}\Psi+V\Psi\]做替换
\[p\rightarrow\hat p=-i\hbar\frac{\partial}{\partial q}\] \[H\rightarrow\hat H=i\hbar\frac{\partial}{\partial t}\]可得
\[i\hbar\frac{\partial}{\partial t}\Psi=\frac{-\hbar^2}{2m}\nabla^2\Psi+V\Psi\]更快的得到了薛定谔方程
有心力场
死去的高中天体物理在攻击我(好吧其实我那一章学的还算过的去)
上强度!另外我建议物竞生麻利点浇我物理(戴面具拿手枪状)
平方反比向心力是椭圆轨道的几何证明
本节完全from3b1bhttps://www.youtube.com/watch?v=xdIjYBtnvZU&t=23s,每个人都应该去看!!因为我复述出来就大大降维了
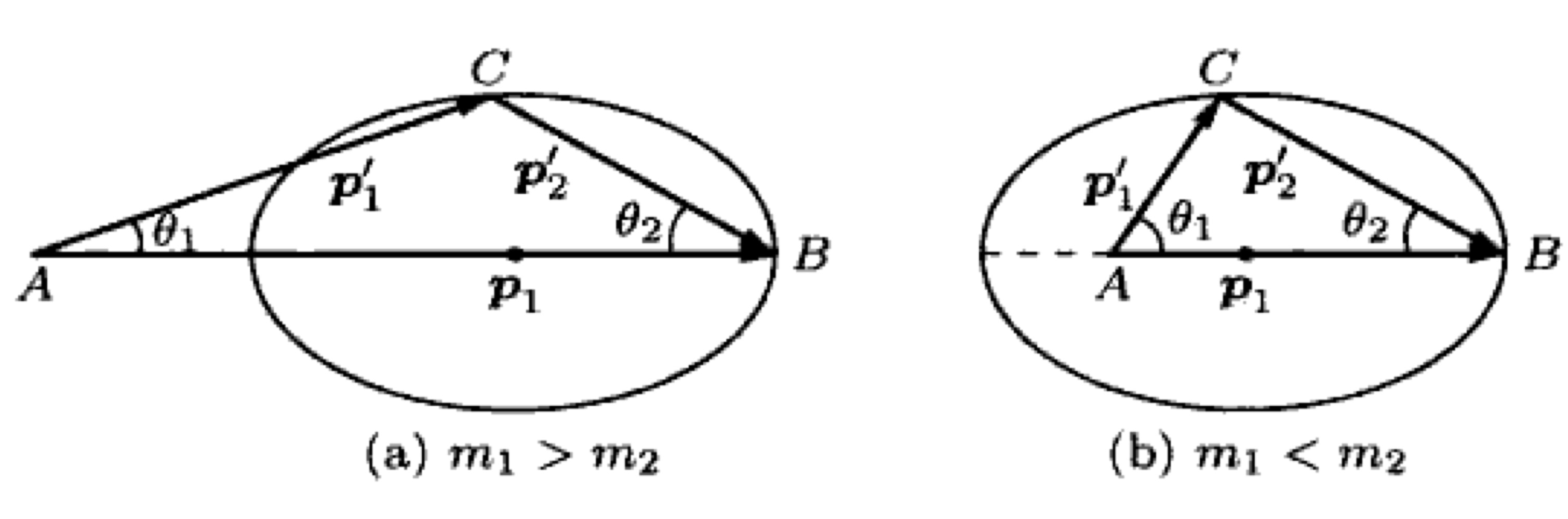
一.圆到椭圆的一种变换方式
这种变化完全是构造性的,在我看来,因为这种变换恰好满足本问题中的所有条件要求,所以在证明中发挥了最关键的作用
取一个圆和圆内的偏心点做一组歪一点的半径
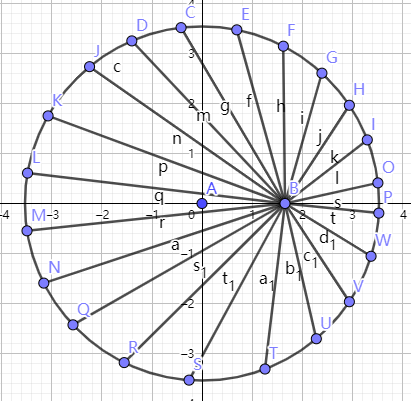
对着每一个歪半径,作中垂线
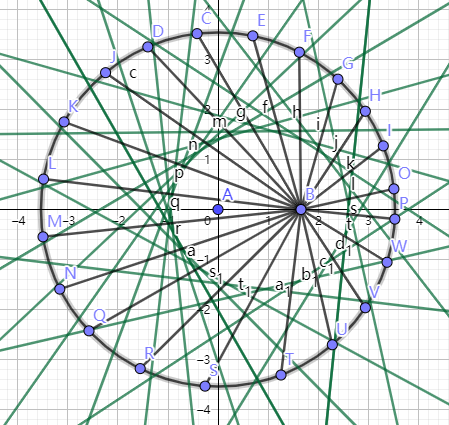
挑出来一根歪半径,可以证明所有中垂线包络了一个以AB为焦点的椭圆,椭圆上一点到两个焦点距离和为半径,每个中垂线(绿色)贡献的切点在半径和中垂线交点上
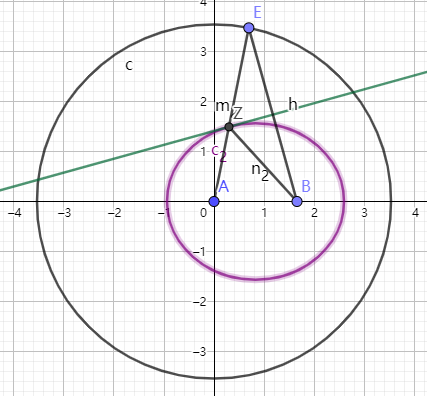
二.将x-θ空间转换到v-θ空间
开普勒第二定律仅仅假设了力始终是向心的,并没有要求轨道形状,可以推出角动量守恒,进而v正比于该点到中心的距离r
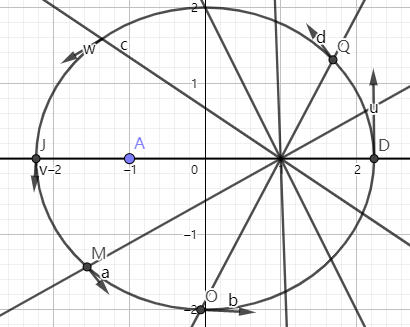
等角度划分位置空间的轨道(dθ->0),这些速度组成了一个序列{v_n}
等角度=》过每一片所需的Δt正比于S正比于r^2
平方反比+牛二=》a=Δv/Δt正比于1/r^2
有这两条之后可以推出划过每一片的速度改变Δv模长是恒定的,再由等角度+向心=》a等角度变化=》Δv的角度与r旋转的角度同步旋转
从近日点D的v0开始,将每次旋转固定角度的Δv_n拼起来,就可以拼出v1,v2,…
并且由r和Δv旋转角度的同步性,远日点的速度恰好在速度空间和v0反向共线;并且从任何一点开始,往前走一固定长度,转固定角度(这角度还是2pi/a,a是整数),最后一定能凑出正多边形;当dθ->0时,多边形变成圆
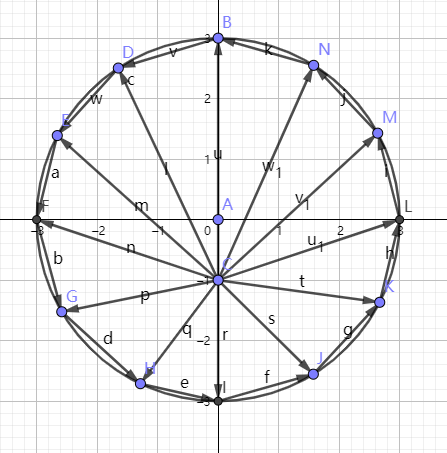
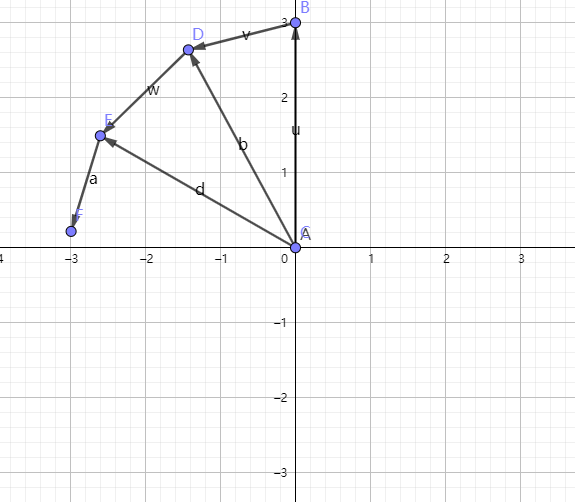
现在仍然不知道原轨道事什么形状,不过可以确定是一个这样的轨道满足:给出一个固定的θ,在原轨道可以得到一个速度(轨道切线方向);在速度空间,表现为圆心A以AB为0角度,逆时针旋转θ引出一条半径;连接该半径在圆上交点和偏心点得到歪半径
要求的轨道就是使得{位置空间得到的切线}恰等于{速度空间歪半径所在直线}}的轨道
为了使θ在两个空间内一致,将速度空间顺时针旋转90度
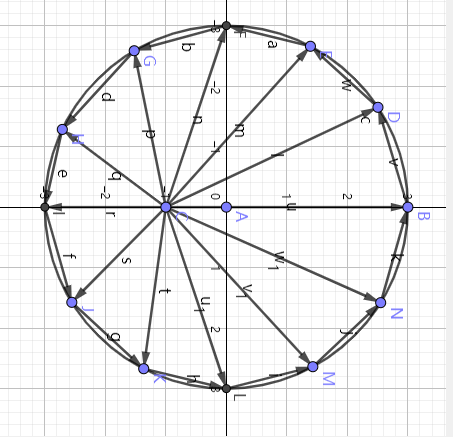
原问题转化为使得{位置空间得到的切线}恰等于{速度空间歪半径所在直线逆时针旋转90°}的轨道
旋转90都会办,问题是以哪为轴旋转呢?这就是个构造性的东西了,先以中点为轴旋转,再证明这恰好是满足条件的
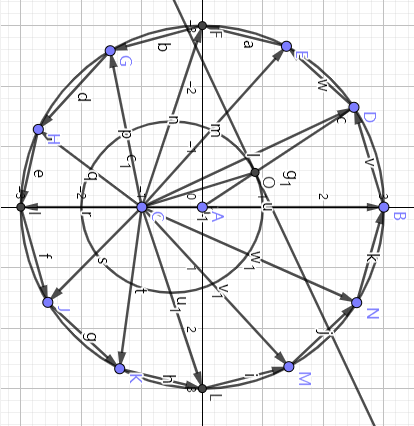
还是和第一部分一样作歪半径的中垂线,围起来了一个椭圆,这个中垂线恰好是圆心引θ半径与轨道交点的切线,和所求的{位置空间得到的切线}给出的逻辑吻合
由此我们在速度空间直接造出了一个满足条件的位置空间,就是一个椭圆,所以椭圆是平方反比向心力下可能的轨道
天体轨道是椭圆的积分证明
本节来自朗道品味,然后我自己爆算(也没那么爆吧)
首先写出能量守恒方程
\[\frac{m}{2}\dot r^2+\frac{mr^2}{2}\dot\theta^2+U(r)=E\]这里的U(r)在传统意义下代表着-GMm/r,我们之后再代入
由角动量守恒
\[J=mr^2\dot\theta\Rightarrow\dot\theta=\frac{J}{mr^2}(*)\]代入到能量守恒式子中
\[\frac{m}{2}\dot r^2+\frac{J^2}{2mr^2}+U(r)=E\]把r·解出来
\[\frac{dr}{dt}=\pm\sqrt{\frac{2}{m}E-\frac{J^2}{m^2r^2}-\frac{2}{m}U(r)}\]由*式
\[\frac{d\theta}{dt}=\frac{J}{mr^2}\]发现这两个微商式子右边都只有r,所以两式相除把dt消掉,把dr当积分量写作
\[\theta(r)=\pm\int\frac{\frac{J}{r^2}dr}{\sqrt{2m(E-U(r))-\frac{J^2}{r^2}}}\]是时候把U(r)=-GMm/r代入准备积分了
\[\theta(r)=\pm\int\frac{\frac{J}{r^2}dr}{\sqrt{2mE+\frac{2GMm^2}{r}-\frac{J^2}{r^2}}}\]老套路倒代换,令u=1/r,则r=1/u,dr=(-1/u^2)du
\[\theta=\pm\int\frac{-du}{\sqrt{2mE/J^2+(2GMm^2/J^2)u-u^2}}\]联想一下$arccos’x=-\frac{1}{\sqrt{1-x^2}}$,把分母配方往这里凑就好了,只看分母
\[\begin{aligned} 2mE/J^2+(2GMm^2/J^2)u-u^2 & = -(u^2-(2GMm^2/J^2)u+\frac{G^2M^2m^4}{J^4}-\frac{G^2M^2m^4}{J^4})+2mE/J^2 \\ & = \frac{G^2M^2m^4}{J^4}+2mE/J^2-(u-\frac{GMm^2}{J^2})^2 \end{aligned}\]下面先积一下这个
\[\int\frac{-dx}{\sqrt{A-Bx^2}}=\frac{1}{\sqrt{A}}\frac{\sqrt{A}}{\sqrt{B}}\int\frac{-d\frac{\sqrt{B}}{\sqrt{A}}x}{\sqrt{1-\frac{B}{A}x^2}}=\frac{1}{\sqrt{B}}arccos\frac{\sqrt{B}}{\sqrt{A}}x+C\]我第一遍漏了个平方才搞这么麻烦,其实这一步没必要这么夸张
代入
\[A=\frac{G^2M^2m^4}{J^4}+2mE/J^2\] \[B=1\] \[x=u-\frac{GMm^2}{J^2}\] \[\theta=\pm arccos[\frac{u-\frac{GMm^2}{J^2}}{\sqrt{\frac{G^2M^2m^4}{J^4}+2mE/J^2}}]+C\]整理一下
\[\frac{u-\frac{GMm^2}{J^2}}{\sqrt{\frac{G^2M^2m^4}{J^4}+2mE/J^2}}=\pm cos(\theta-C)\] \[\frac{1}{r}=u=\frac{GMm^2}{J^2}\pm\sqrt{\frac{G^2M^2m^4}{J^4}+2mE/J^2} cos(\theta-C)\] \[r=\frac{J^2/GMm^2}{1\pm(\sqrt{G^2M^2m^4+2mEJ^2}/GMm^2)cos(\theta-C)}\]满足椭圆极坐标
\[r=\frac{ep}{1+ecos\theta}\]其中
\[e=\sqrt{G^2M^2m^4+2mEJ^2}/GMm^2=\sqrt{1+\frac{2EJ^2}{G^2M^2m^3}}\] \[p=J^2/\sqrt{G^2M^2m^4+2mEJ^2}\]天体定量能量-轨道分析
从上面e(离心率)的表达式中反解出e
\[E=\frac{G^2M^2m^3}{2J^2}(e^2-1)\]当$-\frac{G^2M^2m^3}{2J^2}<E<0$时,$0<e<1$轨道是椭圆
当E=0时,e=1,轨道是抛物线
当E>0时,轨道是双曲线
利用轨道验证开普勒第三定律
只验证椭圆情况(E<0)
由$p=\frac{a^2-c^2}{c};e=\frac{c}{a}$解得
\[a=\frac{ep}{1-e^2}=-\frac{J^2/GMm^2}{2EJ^2/G^2M^2m^3}=-\frac{1}{2E/GMm}=-\frac{GMm}{2E}\] \[\Rightarrow a^3=G^3M^3(\frac{m}{-2E})^3\] \[b=a\sqrt{1-e^2}=-\frac{GMm}{2E}\sqrt{-\frac{2EJ^2}{G^2M^2m^3}}=\sqrt{\frac{1}{-2Em}}J\] \[S=\pi ab=\pi GMJ\frac{\sqrt{m}}{-2E\sqrt{-2E}}\]角动量守恒=》
\[\frac{d\theta}{dt}=\frac{J}{mr^2}\] \[\frac{dS}{dt}=\frac{1}{2}r^2\frac{d\theta}{dt}=\frac{J}{2m}\] \[T=S/\dot S=2\pi GMm\frac{\sqrt{m}}{-2E\sqrt{-2E}}\] \[T^2=4\pi ^2G^2M^2\frac{m^3}{(-2E)^3}=4\pi ^2a^3/ GM\]所以就验证了
\[\frac{T^2}{a^3}=4\pi^2/GM\]比奈公式&天体轨道微分方程
比奈公式将天体运动方程中的t消去,给出了轨道(r-θ)满足的方程
作倒代换u=1/r,结合运动方程,有
\[m\ddot r-mr\dot \theta^2=-\frac{dU}{dr}=F(r)~~(*)\] \[J=mr^2\dot\theta\Rightarrow\dot\theta=\frac{J}{m}u^2\Rightarrow\dot\theta=\frac{J}{mr^2}\]以θ为中间变量求r··:
\[\dot r=\frac{dr}{d\theta}\dot\theta=\frac{d}{d\theta}(\frac{1}{u})\frac{J}{m}u^2=-\frac{1}{u^2}\frac{du}{d\theta}\frac{J}{m}u^2=-\frac{J}{m}\frac{du}{d\theta}\] \[\ddot r=\frac{d}{d\theta}(-\frac{J}{m}\frac{du}{d\theta})\dot\theta=-\frac{J}{m}\frac{d^2u}{d\theta^2}\frac{J}{m}u^2=-\frac{J^2}{m^2}u^2\frac{d^2u}{d\theta^2}\]将r··和J代入*式
\[-\frac{J^2}{m}u^2\frac{d^2u}{d\theta^2}-\frac{J^2u^3}{m}=F(r)\] \[-F(r)=\frac{J^2}{m}u^2(\frac{d^2u}{d\theta^2}+u)\]这就是比奈公式,结束(就这?)
代入F=-GMm/r^2即可得到开普勒问题轨道微分方程

我没有算出A和B,只是给出了椭圆的形式;更具体的轨道方程在上一节积分法
波特兰定理(稳定闭合轨道)
本节from Goldstein以及上课以及阿诺德
在本节中设势能形式为$U(r)=\frac{k}{r^n}$,求出任何可能的n,使得物体在有心力的运动是1.稳定2.圆轨道
先把背景翻译成物理语言
从拉氏量出发
\[L=\frac{m}{2}(\dot r^2+r^2\dot\theta^2)-U(r)\]原运动方程
\[\frac{d}{dt}\frac{\partial L}{\partial \dot r}=\frac{\partial L}{\partial r}\Rightarrow m\ddot r=mr\dot \theta^2-\frac{dU}{dr}\] \[J=\frac{\partial L}{\partial\dot\theta}=mr^2\dot\theta=const\Rightarrow\dot\theta=\frac{J}{mr^2}\]为了凑一个有效势,把mrθ点方积一下
\[mr\dot\theta^2=mr\frac{J^2}{m^2r^4}=\frac{J^2}{mr^3}\] \[\int\frac{J^2}{mr^3}dr=-\frac{J^2}{2mr^2}\]所以把原运动方程第一个式子改写作
\[m\ddot r=-\frac{d}{dr}[U(r)+\frac{J^2}{2mr^2}]=-\frac{d}{dr}V_{eff}(r)\]把题中这两个要求也翻译一下,设半径稳定在r_0运动
稳定
\[\frac{d^2}{dr^2}V_{eff}(r_0)>0~~(1)\]圆
\[\dot r=0\Leftrightarrow\frac{d}{dr}V_{eff}(r_0)=0~~(2)\]也就是说V在r0处有个最小值呗,把$U(r)=-\frac{k}{r^n}$代入,解(2)
\[n\frac{k}{r_0^{n+1}}=\frac{J^2}{mr_0^3}(3)\]解(1)
\[\frac{-n(n+1)k}{r^{n+2}}+\frac{3J}{mr^4}>0\] \[\frac{3}{r}·\frac{J^2}{mr^3}>\frac{n(n+1)k}{r^{n+2}}\]将(3)式代入
\[\frac{3}{r}·\frac{nk}{r^{n+1}}>\frac{n(n+1)k}{r^{n+2}}\]假设n>0,解得
\[0<n<2\]n是整数时,n=1,也就是平方反比力场(天体、电荷)如果受到微扰,则物体会在轨道周围做简谐运动(画❀)
开普勒可以偷懒证,就求了个V(r)最小值,(事实上巨大不严谨,并没有排除n非整数的情况,Goldstein附录里有详细证明太长了啊)但是要求出胡克F=kx我就没找到偷懒办法。。还是看看阿诺德怎么证的吧(他把m全部搞成1了)
由保守系统中的机械能守恒,
\[\frac{1}{2}\dot r^2=E-V_{eff}\]下面把$V_{eff}$简写为V了,不过要记住里面含有角动量的等效势能
\[\frac{dr}{dt}=\sqrt{2(E-V)}\] \[t=\int_{r_0}^{r_1}\frac{dr}{\sqrt{2(E-V)}}\]要找角度的积分关系,所以从角度对时间导数入手,把t看作中间变量消去
\[J=r^2\dot\theta\Rightarrow\frac{d\theta}{dt}=\frac{J}{r^2}\Rightarrow d\theta=\frac{J}{r^2}dt\] \[\theta=\int_{r_0}^{r_1}\frac{Jdr}{r^2\sqrt{2(E-V)}}\]现在关注的问题是轨道是否闭合,所以考虑物体在近日点到远日点转过的角度Φ
\[\Phi=\int_{r_{min}}^{r^{max}}\frac{Jdr}{r^2\sqrt{2(E-V)}}\]如果有
\[\Phi·\frac{a}{b}=2\pi\]其中b,a是正整数;那么走b个Φ就算绕了a圈,轨道闭合
数论喵(x
下面有点不说人话,我用我能听懂的话再写了一遍,看不懂的话自己去看阿诺德p27
引理1:近日点到远日点转过的角度Φ 等于 {将r替换成J/x产生的力学问题振动半周期}
\[W(x)=U(M/x)+x^2/2\]\[T/2=\int_{x_{min}}^{x_{max}}\frac{dx}{\sqrt{2(E-V)}}\]没别的,只是告诉你做个J/x或者说J/r这个变换,系统还是对称的(诺?)
变量代换$x=M/r$,负号当然不管了,T/2回到了上面推出的Φ的形式
引理2:接近半径为r的运动的Φ
\[\Phi_{cir}=\pi J/(r^2\sqrt{V''(r)})=\pi\sqrt{U'/(3U'+rU'')}\]先求物体在平衡位置r0附近做小振动的频率
我比较高中思维,先令物体偏离平衡位置一个小的dr,再算因此受到的回复力和dr之间的系数
在r0处,受力为$-\frac{dV}{dr}(r_0)$
在r0+dr处,受力为$-\frac{dV}{dr}(r_0+dr)$
因此收到的回复力$dF=\frac{dV}{dr}(r_0)-\frac{dV}{dr}(r_0+dr)$
回复力与位移的比为$\frac{dF}{dr}=(\frac{dV}{dr}(r_0)-\frac{dV}{dr}(r_0+dr))/dr=V’‘(r_0)$这玩意就是简谐运动中的w^2
所以半周期走过的角度就是(pi/w)再乘上角速度θ·=J/r^2
\[\Phi_{cir}=\pi J/(r^2\sqrt{V''(r)})\]再来算第二个等号
通过r不变,解方程$V’(r)=0$可得关系
\[U'=\frac{J^2}{r^3}(*)\]把V’‘打开,代入*式
\[V''=U''+\frac{3J^2}{r^4}=U''+\frac{3}{r}U'\]再代到含V‘’的式子里就有了最后的形式,本引理得证
引理3:对于U(r)的哪些特殊形式,可以使得$\Phi_{cir}$与r无关?
也就是说$U’/(3U’+rU’’)=K(const)$
\[(1-3K)U'=KrU''\]等式两边必定对r是齐次的,观察到右边多了一阶导,又补了个r,合理联想到幂函数求导降一个次
这个式子包含一阶二阶,别忘了0阶取对数形式,一二阶导还是幂函数,所以U可以是
\[U(r)\propto r^n(n>=-2,n\neq0)~~or~~U(r)\propto lnr\]考虑第一种形式,从U’到U’‘会落下来常数α-1,所以
\[U'/(3U'+rU'')=1/(3+n-1)=1/(n+2)\] \[\Phi_{cir}=\pi/\sqrt{n+2}\]再算对数情况,发现可以归并到上面的形式,只需令α=0
特例:开普勒pi,胡克pi/2(之前在正则变化证过这个结论)
引理4:设当r->∞时有U->∞,求证
\[lim_{E->\infty}\Phi=\pi/2\]对原式
\[\Phi=\int_{r_{min}}^{r^{max}}\frac{Jdr}{r^2\sqrt{2(E-V)}}\]做代换$y=x/r_{max},r=yr_{max}$
\[\Phi=\int_{y_m}^1\frac{Jdy}{y^2r_{max}\sqrt{2(E-V)}}\]把外面杂七杂八的塞到根号里面(联系引理1的倒代换),令
\[W^*(y)=\frac{y^2}{2}+\frac{1}{r_{max}^2}U(\frac{J}{yr_{max}})\]用到条件E->∞,xmax->∞,W*的第二项可以丢掉;可将Φ化为
\[\Phi=\int_{y_m}^1\frac{dy}{\sqrt{2(W^*(1)-W^*(y))}}\]引理5:U(r)=-kr^{-β},0<β<2,则
\[\Phi_0=\lim_{E->-\infty}\Phi=\int_0^1\frac{dx}{\sqrt{x^\beta-x^2}}=\pi/(2-\beta)\]有了以上一大堆引理之后,正常人应该都看懵了,不是,是可以推稳定封闭力场的U形式了
引理3框出了U只可能为r^n(n>=-2)或lnr(认为n=0)这两种情况,这两种情况均有$Φ=\pi/\sqrt{n+2}$;要使轨道闭合,Φ必须可以表示成pi的有理倍的形式
分类讨论一下,采用极限分析,毕竟稳定闭合不管你E是啥转过的角度都只和n有关
当n>0时,也就是有当r->∞时有U->∞,套引理4可得$Φ=\pi/\sqrt{n+2}=\pi/2$=>n=2
n=0时根号二不是有理数,不考虑
n<0时套引理5,$\sqrt{n+2}=n+2$(0<n+2<2),解得n=-1
综上三种情况,n只能为2或-1
我有一种做了高考导数压轴的感觉。。。首先写出接近圆轨道条件下的Φ表达式,这个Φ很显然是对r连续的,r属于R,Φ同样能在R中完备
但是闭合条件要求Φ在piQ域中,which是在R中不完备的,所以不能让r随便调控Φ,自然能想到这个Φ其实是不随r变化的,由这个条件框定了U肯定是幂函数的形式,并且还进一步把Φ简化到只和幂指数n有关的形式
但是我们还是不知道Φ具体是多少,这时轮到极限分析上场,通过对E取极限可以扔掉部分项,分情况算出Φ的具体值
最后将具体值与Φ(n)对比就可以解出n了
势能微扰问题积分解(水星进动的初等解)
本节来自朗道品味
原先的势能写作$U(r)=-a/r$,现在势能加上一个$\delta U$,求在δU->0时再次回到近日点时与上一个近日点的角度差Δφ的近似值。计算δU取β/r^2和γ/r^3两种情况
首先由上面的一些讨论有了
\[\theta(r)=\pm\int\frac{\frac{J}{r^2}dr}{\sqrt{2m(E-U(r))-\frac{J^2}{r^2}}}\]设
\[g(U)=\sqrt{2m(E-U(r))-\frac{J^2}{r^2}}\]则
\[dr=\frac{r^2}{J}g(U)d\theta\]相邻两次近日点所转过的角度
\[\varphi=2\int_{r_{min}}^{r_{max}}\frac{Jdr}{r^2\sqrt{2m(E-U(r))-\frac{J^2}{r^2}}}\]下面出现一个神级处理:为了避免虚假发散把被积函数做J的偏积分,写出来是这样的
\[\varphi=-2\frac{\partial}{\partial J}\int_{r_{min}}^{r_{max}}g(U)dr\]这是为了方便下一步的对g(U)泰勒展开收敛
先将g^2=h(r)(看作r主元)在r0处展开
这个积分要把被积函数泰勒展开的数学基础在于,把这个积分看作复平面上的围道积分,则围道可以随便变的前提是满足小狐引理,具体请看https://www.zhihu.com/question/545755276/answer/2599472649
h(r0+r)=h(r0)+h’(r0)r+O(r),其中h(r0)=0,所以g~根号(r-r_0)
小狐引理要求被积函数展开的一阶项乘(r-r_0)在r->r0时趋于0,如果不做神级操作,展开项含1/g^3,把h的近似表达式代入,得展开项是r-r0的-3/2阶,乘上r-r0后仍然是r-r0的负幂次,小狐引理不能使用
而做了神级操作之后在不展开时的被积函数就被拉高为g的正1幂次,再对U展开,求导一次出现分母一个根号,也就是r-r0的-1/2阶,乘上r-r0后是他的正幂次,同向趋于0,可以使用小狐引理
对g(U)在-a/r处泰勒展开
\[g'(U)=-\frac{m}{g(U)}\] \[g'(-a/r)=-\frac{m}{g(-a/r)}\] \[g(-a/r+\delta U)=g(-a/r)-\frac{m}{g(-a/r)}\delta U+O(\delta U)\]由于对第一项的积分恰为无扰时的2pi,所以在扰动很小时,Δφ近似于第二项积分
\[\Delta\varphi=-2\frac{\partial}{\partial J}\int_{r_{min}}^{r_{max}}-\frac{mdr}{g(-a/r)}\delta U\]对原表达式进行换元dr->dθ:$dr=\frac{r^2}{J}g(U)d\theta$
\[\Delta\varphi=2\frac{\partial}{\partial J}\int_{r_{min}}^{r_{max}}\frac{mr^2\delta U}{J}dr=2\frac{\partial}{\partial J}\frac{m}{J}\int_0^\pi r^2\delta Ud\theta\]当δU=β/r^2时
\[\Delta\varphi=2\frac{\partial}{\partial J}\frac{m\beta\pi}{J}=-\frac{2m\beta\pi}{J^2}\]当ΔU=γ/r^3时
\[\Delta\varphi=2\frac{\partial}{\partial J}\frac{m\gamma}{J}\int_0^\pi 1/rd\theta\]现在需要找到1/r与θ的关系,联想到之前的轨道方程极坐标表达
\[r=\frac{ep}{1-ecos\theta}\Rightarrow\frac{1}{r}=\frac{1-ecos\theta}{ep}\] \[\Delta\varphi=2\frac{\partial}{\partial J}\frac{m\gamma}{Jep}\int_0^\pi 1-ecos\theta d\theta=2\frac{\partial}{\partial J}\frac{m\gamma\pi}{Jep}\]其中,$ep=J^2/am,Jep=J^3/am$
\[\Delta\varphi=2\frac{\partial}{\partial J}\frac{am^2\gamma\pi}{J^3}=\frac{-6am^2\gamma\pi}{J^4}\]平直时空的潮汐力
本节来自sz学长的note&梁灿彬,rewrite by我自己
三维平直空间下的引力势
\[\phi=-\frac{GM}{r}=-\frac{GM}{\sqrt{x^2+y^2+z^2}}\]牛二
\[\frac{d^2x^i}{dt^2}=\frac{F^i}{m}\]引力场中受力
\[\frac{F^i}{m}=-(\nabla\phi)_i=-\delta^{ij}\partial_j\phi\]其中δ是平直空间中的度规,起到升指标的作用
代入牛二可得在$\vec x$中的加速度表达为
\[\frac{d^2x^i}{dt^2}=-\delta^{ij}\partial_j\phi|_{\vec x}\]令$\vec x$偏移一个极小的位移$\vec n$,则在x+n处的加速度为
\[\frac{d^2(x^i+n^i)}{dt^2}=-\delta^{ij}\partial_j\phi|_{\vec x+\vec n}\]两式做差可得x处位移n引起的加速度微小改变量为(改写成微商乘小改变的形式)
\[\frac{d^2n^i}{dt^2}=-\delta^{ij}(\partial_j\phi|_{\vec x+\vec n}-\partial_j\phi|_{\vec x})=-\delta^{ij}n^k\partial_k\partial_j\phi|_{\vec x}=-n^k\partial_k\partial^i\phi\]更进一步的来讲,求潮汐加速度的过程也是在求引力场中某点由于微小位移偏差产生的加速度
接下来就是一个个求偏导,把Φ的表达式带进去
\[\frac{\partial\phi}{\partial x^i}=\frac{GM}{r^3}x_i\] \[\frac{\partial}{\partial x^j}\frac{\partial\phi}{\partial x^i}=-\frac{3GM}{r^5}x_jx_i+\frac{GM}{r^3}\delta _{ij}\] \[\frac{d^2n^i}{dt^2}=-\delta^{ij}n^k(-\frac{3GM}{r^5}x_kx_j+\frac{GM}{r^3}\delta_{kj})=\frac{3GM}{r^5}x^in^kx_k-\frac{GM}{r^3}n^i\]计算一些特例
\[\frac{d^2n^1}{dt^2}=-n^k(-\frac{3GM}{r^5}x_kx_1)-\frac{GM}{r^3}n^1=-\frac{GM}{r^3}n^1+\frac{3GM}{r^5}x^1(n^1x_1+n^2x_2+n^3x_3)\]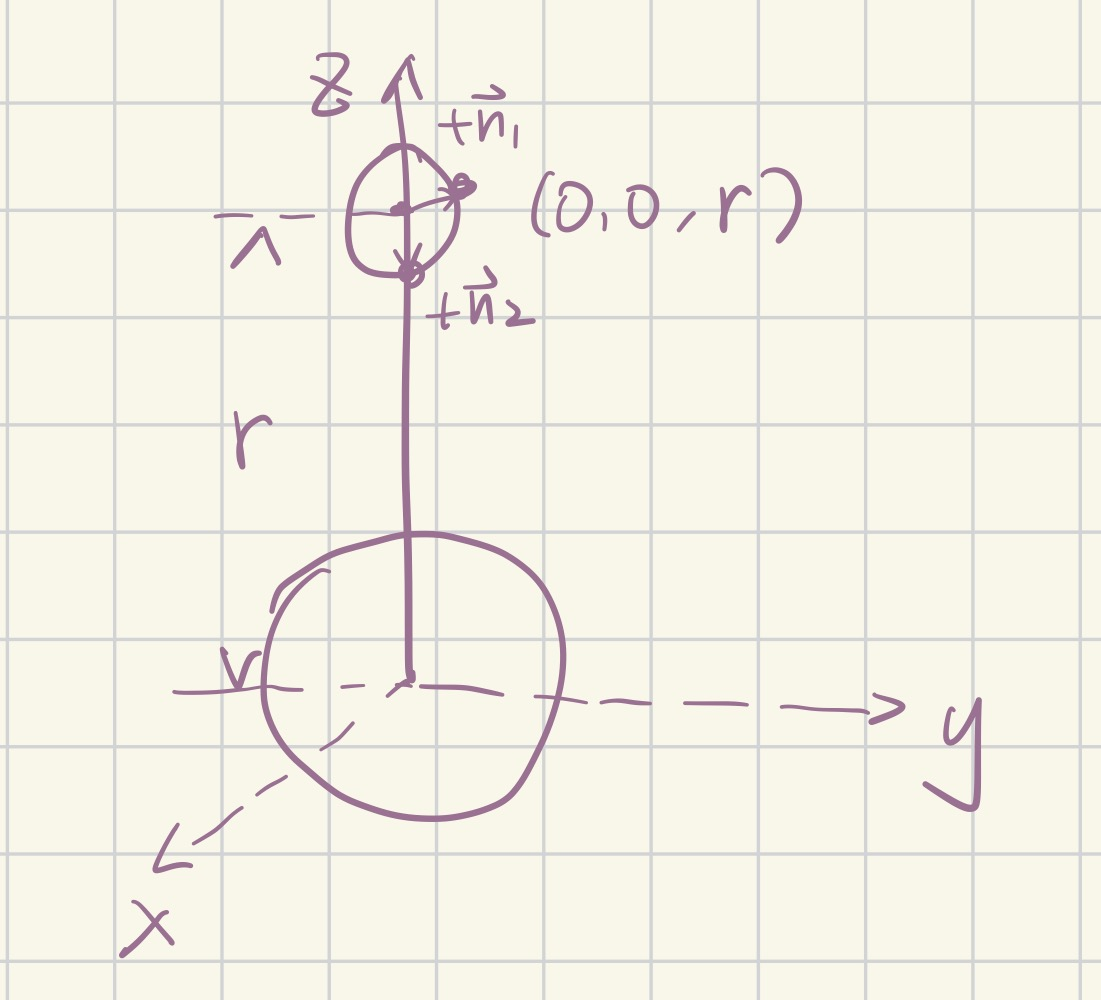
在潮汐力问题中,规定创造引力场Φ的质心位于坐标原点;探测场的点在z轴上,坐标$\vec P=(0,0,r)$,那么在p点处潮汐加速度的表达式(n的上标全是指标不是幂次,r的带的是幂次)
\[\frac{d^2n^1}{dt^2}|_{\vec P}=-\frac{GM}{r^3}n^1\] \[\frac{d^2n^2}{dt^2}|_{\vec P}=-\frac{GM}{r^3}n^2\] \[\frac{d^2n^3}{dt^2}|_{\vec P}=-\frac{GM}{r^3}n^3+\frac{3GM}{r^3}n^3=\frac{2GM}{r^3}n^3\]可见x、y方向偏移导致的加速度是“向心”的,而z方向偏移导致的加速度是“离心”的,这正好应证了直观上潮汐力的来源:因为引力的空间分布不均匀导致的“撕裂”效果
从测地偏离到爱因斯坦场方程
可能会拖更,不确定我自己能不能吃透,说不定一万年之后再补全;但是看lcb看到潮汐可以搞出爱因斯坦场方程给我看高潮了。。
先来推导一下牛顿引力势的拉普拉斯(知乎显示不出来环面积分oiint,知乎端读者自行脑补)
类比电的高斯定理
\[\oiint \vec E\cdot \vec{dS}=\frac{1}{\varepsilon_0}\iiint\rho_edV=\frac{1}{4\pi\varepsilon_0}\iiint4\pi\rho_edV\]电场中
\[F=\frac{1}{4\pi\varepsilon_0}\frac{q_1q_2}{r^2}\]引力场中
\[F=G\frac{Mm}{r^2}\]平推过来
\[\oiint\vec{\nabla\phi}\cdot\vec{dS}=\iiint4\pi G\rho dV\]由高斯积分公式
\[\oiint \vec F·\vec{dS}=\iiint(\vec\nabla\cdot\vec F)dV\]可得
\[\iiint(\nabla·\nabla\phi )dV=\iiint4\pi G\rho dV\]即
\[\nabla^2\phi=4\pi G\rho\]再来看看黎曼张量
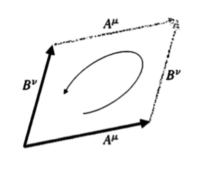
矢量V在无挠流形中沿着这样的(A->B->(-A)->(-B))闭合四边形平移之后会和原来的有差,把这个差记作
\[\delta V^\rho=R^\rho_{\sigma\mu\nu}V^\sigma A^\mu B^\nu\]其中δV是一个整体向量,$R^\rho_{\sigma\mu\nu}$被称为黎曼张量。拆开来看看,最上面的ρ代表分量,不用管,下面的三个指标依次代表被平移的矢量、平移方向(分先后)可以看出R是关于uv反对称的
下面用方向导数和联络那一套重新表示上面的平移过程
将矢量V沿着A^\mu平移,改变的量为
\[\delta V^\rho=A^\mu\nabla_\mu V^\rho\]类似于dy=y’ dx的拆开写法
以此类推,用导数的方式描述上面的平移过程(A->B->(-A)->(-B)),有
\[\delta X^\rho=(\nabla_\mu\nabla_\nu-\nabla_\nu\nabla_\mu)V^\rho\\ =(\partial_\mu\Gamma_{\nu\sigma}^\rho+\Gamma_{\mu\lambda}^\rho\Gamma_{\nu\sigma}^\lambda-(\mu\leftrightarrow\nu))-2\Gamma_{[\mu\nu]}^\lambda\nabla_\lambda V^\rho\]这个式子实际上是最初那个几何表述的二阶微分形式,要联系起来的话也即$A^\mu B^\nu\delta X^\rho=\delta V^\rho$
所以定义
\[[\nabla_\mu,\nabla_\nu]V^\rho:=R^\rho_{\sigma\mu\nu}V^\sigma-T^\lambda_{\mu\nu}\nabla_\lambda V^\rho\]其中T是挠度张量,在Levi-Civita联络下为0,此时
\[[\nabla_\mu,\nabla_\nu]V^\rho:=R^\rho_{\sigma\mu\nu}V^\sigma\]从联络的角度考虑,黎曼张量描述了联络的方向导数的对易子(也许不能叫对易子?应该是指标轮换差),也即
\[R^\rho_{\sigma\mu\nu}=\nabla_{[\mu}\Gamma_{\nu]\sigma}^\rho\]这个式子看上去不错,可以直接读出来R关于mu nu反对称,下面展开一下
\[R^\rho_{\sigma\mu\nu}=\partial_\mu\Gamma_{\nu\sigma}^\rho-\partial_\nu\Gamma_{\mu\sigma}^\rho+\Gamma_{\mu\lambda}^\rho\Gamma_{\nu\sigma}^\lambda-\Gamma_{\nu\lambda}^\rho\Gamma_{\mu\sigma}^\lambda\]这就是黎曼张量的展开式,可以当作定义式
接下来令mu=rho缩并一下
\[R_{\sigma\nu}:=R^\rho_{\sigma\rho\nu}=\partial_\rho\Gamma_{\nu\sigma}^\rho-\partial_\nu\Gamma_{\rho\sigma}^\rho+\Gamma_{\rho\lambda}^\rho\Gamma_{\nu\sigma}^\lambda-\Gamma_{\nu\lambda}^\rho\Gamma_{\rho\sigma}^\lambda\]如果有需要的话可能要运用到克氏符的缩并继续展开,但是我觉得这展开又长又丑,不写了
\[\Gamma_{\rho\lambda}^\rho=\frac{1}{2}g^{\rho\mu}\partial_\lambda g_{\rho\mu}\]再定义里奇标量
\[R:=g^{\mu\nu}R_{\mu\nu}\]借用平直的潮汐力表达式
\[\frac{d^2n^i}{dt^2}=-n^k\partial_k\partial^i\phi\]平推到广相中,势场丢掉,只关注向量n的平移改变量;$\partial$对应$Z\nabla$(Z的地位是速度,向量对参数求导;nabla地位是方向导数,这是一个链式法则)
\[a^c=Z^a\nabla_a(Z^b\nabla_b r^c)\]这种写法下的测地线方程写作,待会要代入的
\[Z^a\nabla_aZ^b=0\]
用这个把最初始的式子括号里的换一遍
\[Z^a\nabla_ar^b=r^a\nabla_aZ^b\] \[a^c=Z^a\nabla_a(r^b\nabla_bZ^c)=(Z^a\nabla_ar^b)\nabla_bZ^c+r^bZ^a\nabla_a\nabla_bZ^c\]利用黎曼张量
\[(\nabla_a\nabla_b-\nabla_b\nabla_a)Z^c=R_{dab}^cZ^d\Rightarrow\nabla_a\nabla_bZ^c=R_{dab}^cZ^d+\nabla_b\nabla_aZ^c\] \[a^c=(Z^a\nabla_ar^b)\nabla_bZ^c+r^bZ^aR_{dab}^cZ^d+r^bZ^a\nabla_b\nabla_aZ^c\]再用一次协变对易(说实话这式子我不太懂)
\[(Z^a\nabla_ar^b)\nabla_bZ^c=(r^a\nabla_aZ^b)\nabla_br^c\] \[a^c=(Z^a\nabla_ar^b)\nabla_bZ^c+r^bZ^aR_{dab}^cZ^d+r^bZ^a\nabla_b\nabla_aZ^c\]对测地线方程求全导数
\[r^b\nabla_b(Z^a\nabla_aZ^c)=(r^b\nabla_bZ^a)\nabla_aZ^c+r^bZ^a\nabla_b\nabla_aZ^c=0\]调整第一项的哑变量后可完美带入a的表达式,得到
\[a^c=R_{dab}^cZ^dr^bZ^a=-R_{dba}^cZ^dr^bZ^a\]再次将他与牛顿引力潮汐对比
\[\frac{d^2n^i}{dt^2}=-n^k\partial_k\partial^i\phi\]可见
\[R_{dba}^cZ^dZ^a\leftrightarrow\partial_k\partial^i\phi\]现在要对这两个潮汐力平行地作缩并,联系到先前的$\nabla^2\phi=4\pi G\rho$,看来是要对一个最后留下来的最上面的指标和循环指标缩并;然而R的上下缩并本质只有一种是非平凡的,也即里奇张量R_da
\[R_{da}Z^dZ^a\leftrightarrow\nabla^2\phi=4\pi G\rho\]Z的地位相当于速度(对参量求过一阶导),这时候想做一个操作来“同除”ZaZb,那么就在右侧创造一个张量$T_{da}$,使得$T_{da}Z^dZ^a=\rho$
\[R_{da}Z^dZ^a\leftrightarrow(\nabla^2\phi/\rho)T_{da}Z^dZ^a=4\pi GT_{da}Z^dZ^a\]发现能动张量正好能满足这个形式;能动张量(指标升过)的表达式$T_\mu^\nu=\partial_\mu q\frac{\partial L}{\partial(\partial_\mu q)}-\delta_\mu^\nu L$,这里的L均为密度形式
特殊的,T00=H(哈密顿量或者说能量密度)(0分量是时间,还原到经典力学);能动量守恒被写作$\partial^a T_{ab}=0$
这时候就可以直接猜
\[R_{ab}=4\pi GT_{ab}\]但是问题出在$\nabla^aT_{ab}=0$而$\nabla^aR_{ab}$不该=0(我懒得详细写了,而且我这些基础不太牢,见梁p223)
所以对LHS进行修正,
\[G_{ab}:=R_{ab}-\frac{1}{2}Rg_{ab}\]此时RHS的系数可能会发生改变,先用待定系数k写着,待会用牛顿近似求一下
\[R_{ab}-\frac{1}{2}Rg_{ab}=kT_{ab}(*)\]在平直时空(牛顿近似)下同升指标b
\[R_a^b-\frac{1}{2}\delta_a^bR=kT_a^b\]缩并ab
\[R-2R=-R=kT\Rightarrow R=-kT\]代回*,
\[R_{ab}=kT_{ab}+\frac{1}{2}Rg_{ab}=k(T_{ab}-\frac{1}{2}Tg_{ab})\]作用在速度矢量上
\[R_{ab}Z^aZ^b=k(\rho-\frac{1}{2}Tg_{ab}Z^aZ^b)=k(\rho+\frac{1}{2}T)\simeq k(\rho-\frac{1}{2}\rho)=\frac{1}{2}\rho=\nabla^2\phi=4\pi G\rho\] \[\Rightarrow k=8\pi G\rho\]得到了爱因斯坦场方程
\[G_{ab}=R_{ab}-\frac{1}{2}Rg_{ab}=8\pi GT_{ab}\]改成自然单位制抹掉引力常数G后
\[G_{ab}=R_{ab}-\frac{1}{2}Rg_{ab}=8\pi T_{ab}\]另解:不从潮汐力入手的测地偏离方程
现在抛开潮汐力不谈去思考本质,在上面的过程主要求出了相邻两条测地线由于小小的偏差所导致的相对加速度
不妨直接对测地线方程做差分试试;这是测地线方程
\[\frac{d^2x^\mu}{d\lambda^2}+\Gamma_{\rho\sigma}^\mu \frac{d x^\rho}{d\lambda}\frac{dx^\sigma}{d\lambda}=0(')\]令测地线x产生一个小偏差$\xi^\mu$,则$x^\mu\to x^\mu+\xi^\mu$,为方便运算记Δ为差分算符,且有$Δx^\mu=\xi^\mu$;两个测地线作差分得
\[\frac{d^2\xi^\mu}{d\lambda^2}+\Gamma_{\rho\sigma}^\mu\Delta(\frac{d x^\rho}{d\lambda}\frac{dx^\sigma}{d\lambda})+\Delta\Gamma_{\rho\sigma}^\mu(\frac{d x^\rho}{d\lambda}\frac{dx^\sigma}{d\lambda})=0\] \[\frac{d^2\xi^\mu}{d\lambda^2}+\Gamma_{\rho\sigma}^\mu[(\frac{d x^\rho}{d\lambda}+\frac{d\xi^\rho}{d\lambda})(\frac{dx^\sigma}{d\lambda}+\frac{d\xi^\sigma}{d\lambda})-\frac{d x^\rho}{d\lambda}\frac{dx^\sigma}{d\lambda}]+\xi^\nu\partial_\nu\Gamma_{\rho\sigma}^\mu\frac{d x^\rho}{d\lambda}\frac{dx^\sigma}{d\lambda}=0\]记得第二部分要舍去二阶及以上项(因为偏差是小量)
\[\frac{d^2\xi^\mu}{d\lambda^2}+2\Gamma_{\rho\sigma}^\mu\frac{d x^\rho}{d\lambda}\frac{d\xi^\sigma}{d\lambda}+\xi^\nu\partial_\nu\Gamma_{\rho\sigma}^\mu\frac{d x^\rho}{d\lambda}\frac{dx^\sigma}{d\lambda}=0(*)\]其中的Γ取值在“中心点”x(类似于上上节平直时空中,引力势Φ在中心x处取得;这里的Γ包含了局部场的信息,地位等价于引力势的梯度)
下面利用协变导数的展开把上式整理一下,用到的协变导数展开是
\(\frac{D}{d\lambda}V^\mu=\frac{dx^\rho}{d\lambda}\nabla_\rho V^\mu=\frac{dx^\rho}{d\lambda}\partial_\rho V^\mu+\frac{dx^\rho}{d\lambda}\Gamma_{\rho\sigma}^\mu V^\sigma\) 第一个等号相当于链式法则,第二个等号是协变导数展开
当参数λ=t时,上式左侧的物理意义为V的速度;运用同样的套路对参数求二阶导,再利用{测地线=不受外力物体在弯曲时空中的运动轨迹}这个性质也可以由a=0展开测地线方程
对着这个偏移求个二阶导
\[\frac{D^2}{d\lambda^2}\xi^\mu=\frac{dx^\rho}{d\lambda}\nabla_\rho(\frac{d\xi^\mu}{d\lambda}+\frac{dx^\sigma}{d\lambda}\Gamma_{\nu\sigma}^\mu\xi^\nu)=\frac{d}{d\lambda}(\frac{d\xi^\mu}{d\lambda}+\frac{dx^\sigma}{d\lambda}\Gamma_{\nu\sigma}^\mu\xi^\nu)+\frac{dx^\rho}{d\lambda}\Gamma_{b\rho}^\mu(\frac{d\xi^b}{d\lambda}+\frac{dx^\sigma}{d\lambda}\Gamma_{\nu\sigma}^b\xi^\nu)\] \[=\frac{d^2\xi^\mu}{d\lambda^2}+\frac{d^2x^\sigma}{d\lambda^2}\Gamma_{\nu\sigma}^\mu\xi^\nu+\frac{dx^\sigma}{d\lambda}\frac{dx^\rho}{d\lambda}(\partial_\rho\Gamma_{\nu\sigma}^\mu)\xi^\nu+\frac{dx^\sigma}{d\lambda}\Gamma_{\nu\sigma}^\mu\frac{dx^\rho}{d\lambda}\partial_\rho\xi^\nu+\\ \frac{dx^\rho}{d\lambda}\Gamma_{b\rho}^\mu\frac{dx^\sigma}{d\lambda}\partial_\sigma\xi^b+\frac{dx^\rho}{d\lambda}\frac{dx^\sigma}{d\lambda}\Gamma_{b\rho}^\mu\Gamma_{\nu\sigma}^b\xi^\nu\]将*式和‘式的测地线方程代入消掉对参数的二阶导可得
\[\begin{aligned} &\frac{D^2}{d\lambda^2}\xi^\mu \\ & =-\xi^\nu(\partial_\nu\Gamma_{\sigma\rho}^\mu)\frac{dx^\sigma}{d\lambda}\frac{dx^\rho}{d\lambda}-\Gamma_{\sigma\rho}^b\frac{dx^\sigma}{d\lambda}\frac{dx^\rho}{d\lambda}\Gamma_{\nu\sigma}^\mu\xi^\nu+\frac{dx^\sigma}{d\lambda}\frac{dx^\rho}{d\lambda}(\partial_\rho\Gamma_{\nu\sigma}^\mu)\xi^\nu\\&~~~~-\frac{dx^\sigma}{d\lambda}\Gamma_{\nu\sigma}^\mu\frac{dx^\rho}{d\lambda}\partial_\rho\xi^\nu+\frac{dx^\rho}{d\lambda}\Gamma_{b\rho}^\mu\frac{dx^\sigma}{d\lambda}\partial_\sigma\xi^b+\frac{dx^\rho}{d\lambda}\frac{dx^\sigma}{d\lambda}\Gamma_{b\rho}^\mu\Gamma_{\nu\sigma}^b\xi^\nu \\ \end{aligned}\]只计算Levi-Civita联络(Gamma两个下标可交换),再(向着答案的方向)调换一些循环指标整理一下
\[\frac{D^2}{d\lambda^2}\xi^\mu=-\xi^\nu(\partial_\nu\Gamma_{\sigma\rho}^\mu)\frac{dx^\sigma}{d\lambda}\frac{dx^\rho}{d\lambda}-\Gamma_{\sigma\rho}^b\frac{dx^\sigma}{d\lambda}\frac{dx^\rho}{d\lambda}\Gamma_{\nu\sigma}^\mu\xi^\nu+\frac{dx^\sigma}{d\lambda}\frac{dx^\rho}{d\lambda}(\partial_\rho\Gamma_{\nu\sigma}^\mu)\xi^\nu+\frac{dx^\rho}{d\lambda}\frac{dx^\sigma}{d\lambda}\Gamma_{b\rho}^\mu\Gamma_{\nu\sigma}^b\xi^\nu\\ =(\partial_\rho\Gamma_{\nu\sigma}^\mu)\frac{dx^\sigma}{d\lambda}\frac{dx^\rho}{d\lambda}\xi^\nu-(\partial_\nu\Gamma_{\rho\sigma}^\mu)\xi^\nu\frac{dx^\sigma}{d\lambda}\frac{dx^\rho}{d\lambda}+\Gamma_{\rho b}^\mu\Gamma_{\nu\sigma}^b\frac{dx^\rho}{d\lambda}\frac{dx^\sigma}{d\lambda}\xi^\nu-\Gamma_{\nu b}^\mu\Gamma_{\rho\sigma}^b\frac{dx^\sigma}{d\lambda}\frac{dx^\rho}{d\lambda}\xi^\nu\]利用
\[R^\mu_{\sigma\rho\nu}=\partial_\rho\Gamma_{\nu\sigma}^\mu-\partial_\nu\Gamma_{\rho\sigma}^\mu+\Gamma_{\rho b}^\mu\Gamma_{\nu\sigma}^b-\Gamma_{\nu b}^\mu\Gamma_{\rho\sigma}^b\]进而写作
\[\frac{D^2}{d\lambda^2}\xi^\sigma=R^\mu_{\sigma\rho\nu} \frac{dx^\sigma}{d\lambda}\xi^\nu\frac{d x^\rho}{d\lambda}=-R^\mu_{\sigma\nu\rho} \frac{dx^\sigma}{d\lambda}\xi^\nu\frac{d x^\rho}{d\lambda}\]把所有一阶导项写作Z,即还原到梁灿彬书上的形式
\[a^c=-R_{abd}^cZ^aw^bZ^d\]引力偏转问题
先求偏转角的表达式(很水)
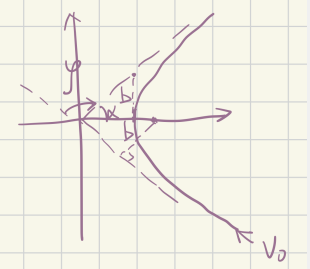
α是渐近线与x轴夹角,φ是偏转角,他们满足的数量关系是α=90°-φ/2
带上tan后,cotα=tanφ/2=a/b,也就是说要通过E=$\frac{mk^2}{2J^2}(e^2-1)$求出$e^2-1=\frac{b^2}{a^2}$
接下来转到物理part
\[E=\frac{m}{2}v_0^2=\frac{mk^2}{2J^2}(e^2-1)\] \[J=mv_0b\] \[\Rightarrow e^2-1=\frac{J^2v_0^2}{k^2}=\frac{b^2}{a^2}\]啪一下很快啊就算出来了
\[tan\frac{\varphi}{2}=\frac{a}{b}=\frac{k}{Jv_0}=\frac{k}{mbv_0^2}=\frac{GM}{bv_0^2}\]散射截面&卢瑟福公式(水)
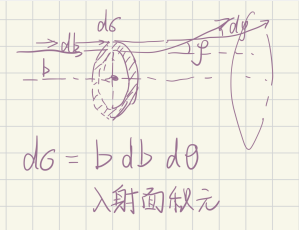
如图所示的dσ是入射面积元(对着θ积分恰好得到环面元2pibdb),下面把这个里面的b全部替换成偏转角φ来表示
\[b=\frac{k}{mv_0^2}\frac{1}{tan\frac{\varphi}{2}}\]\[d\sigma=bdbd\theta=b\frac{db}{d\varphi}d\varphi d\theta=(\frac{k}{mv_0^2})^2\frac{cos\frac{\varphi}{2}}{sin\frac{\varphi}{2}}\frac{-1}{sin^2\frac{\varphi}{2}}(\frac{1}{2})d\varphi d\theta\]在解决其他势的散射问题时,同样要先把b用φ表示出来,剩下的就依葫芦画瓢了
负号是因为b和φ负相关,在这里直接丢掉不管了
\[d\sigma=\frac{1}{2}(\frac{k}{mv_0^2})^2\frac{cos\frac{\varphi}{2}}{sin^3\frac{\varphi}{2}}d\varphi d\theta\]这样就算是把瞄准距离b全部换成偏转角φ了,但是还没结束,蹦出来一个立体角叫$d\Omega=sin\varphi d\varphi d\theta$,那就把上式的d部分代换成dΩ
\[d\sigma=\frac{1}{4}(\frac{k}{mv_0^2})^2\frac{1}{sin^4\frac{\varphi}{2}}d\Omega\]这就是所谓的卢瑟福散射公式了,其中k是平方反比力的系数(觉得这玩意怪怪的不好记,去年推过一次我今年拿到这个名词还反应不过来是怎么回事)
相对论性衰变
前言:相对论性的物理量写法在note上册写了,这里复习几个自然单位制下重要式子
\[E^2=p^2+m^2\] \[p=m\gamma v,E=m\gamma\Rightarrow p=Ev\]
只考虑动力学问题
对于一个质量为M的静止粒子的自发衰变,设衰变后两个粒子的质量和能量分别为m1,E1;m2,E2,则可以列方程
能量守恒
\[M=E_1+E_2\]动量守恒(动量模长相等)
\[E_1^2-m_1^2=E_2^2-m_2^2\]可以用质量解出能量
\[E_1=\frac{M^2+m_1^2-m_2^2}{2M}\] \[E_2=\frac{m^2-m_1^2+m_2^2}{2M}\]在实验系中用能量E1质量m1的粒子轰击静止的m2
\[p_1^2=E_1^2-m_1^2\]总能量
\[E=E_1+m_2\]质心运动速度
\[v=\frac{p}{E}=\frac{p_1}{E_1+m_2}\]下面考虑一个速度V的粒子分解为2个粒子的出射角与其能量之间的关系。设出射粒子在实验室坐标系下能量E动量p($p=\sqrt{E^2-m^2}$),在质心系下能量E0
将动量p分解到运动方向上得到了pcosθ,写出4动量的简化形式(?)便于作洛伦兹变换
\[\begin{pmatrix} -E_0\\ p_0cos\theta_0 \end{pmatrix} =\begin{pmatrix} coshs&sinhs\\ sinhs&coshs \end{pmatrix} \begin{pmatrix} -E\\ pcos\theta \end{pmatrix}\]可得
\[E_0=\frac{-E+Vpcos\theta}{\sqrt{1-V^2}}\]解出角度
\[cos\theta=\frac{E+E_0\sqrt{1-V^2}}{V\sqrt{E^2-m^2}}\]这就已经回答了题目的问题了,下面进一步探讨分裂后的一个粒子在实验室坐标系下,当拥有确定的质量与能量后,3矢量p可能的取值
运用洛伦兹逆变换,将质心坐标系旋转到实验室坐标系,p0,θ0是质心坐标系下物理量
\[\begin{pmatrix} -E\\ p_x \end{pmatrix} =\begin{pmatrix} coshs&-sinhs\\ -sinhs&coshs \end{pmatrix} \begin{pmatrix} -E_0\\ p_0cos\theta_0 \end{pmatrix}\]仅有px方向上存在两个坐标系的相对速度V
\[p_x=\frac{p_0cos\theta_0+E_0V}{\sqrt{1-V^2}}\] \[p_y=p_0sin\theta_0\]其中唯一的自变量是夹角θ0;已经可以看出这是由θ0生成的偏心椭圆了,再整理一下
\[p_x-\frac{E_0V}{\sqrt{1-V^2}}=\frac{p_0}{\sqrt{1-V^2}}cos\theta_0\] \[p_y=p_0sin\theta_0\]长半轴为$p_0\gamma$,短半轴为$p_0$,偏心距$E_0V\gamma$
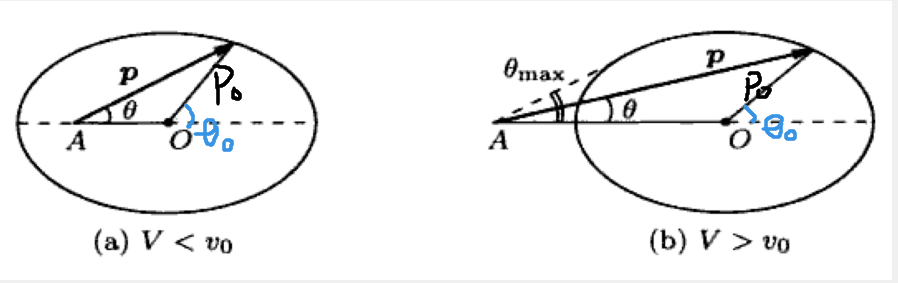
其中,v0是质心坐标系下速度:$v_0=p_0/E_0$;当V>v0(分裂前速度足够相对论、而分裂后携带速度不够大),此时存在散射角极限
\[sin\theta_{max}=\frac{p_0\sqrt{1-V^2}}{mV}\]当V«1时,观察一下退化到非相对论的情况
此时偏心椭圆退化到非偏心的圆
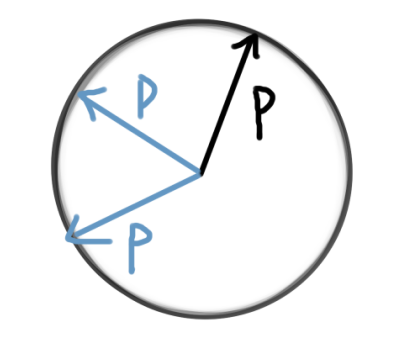
这意味着p长度确定,方向取遍0到2派;这与我们的直觉(E,m均确定时v大小确定,进而p大小确定并且没有取不到的角度)相吻合
更直观的碰撞前后三角形参见下一章
相对论性碰撞
经典部分来自朗道场论
碰前两个粒子:m1,p1,E1;m2,p2,E2;碰撞后的物理量加撇号
则动量能量守恒可以用4动量写作
\[p_1^i+p_2^i={p'}_1^i+{p'}_2^i\]移项$p_1^i+p_2^i-{p’}_1^i={p’}_2^i$,左右取模方
\[-m_1^2+p_{1i}p_2^i-p_{1i}{p'}_1^i-p_{2i}{p'}_1^i=0\]移项$p_1^i+p_2^i-{p’}_2^i={p’}_1^i$,左右取模方
\[-m_2^2+p_{1i}p_2^i-p_{2i}{p'}_2^i-p_{1i}{p'}_2^i=0\]在m2静止的参考系中
\[p_{2i}=(-E_2,0,0,0)\] \[p_2^i=(E_2,0,0,0)\] \[p_{1i}p_2^i=-E_1m_2\] \[p_{2i}{p'}_1^i=-m_2E_1'\] \[p_{1i}{p'}_1^i=-E_1E_1'+\vec p_1\cdot\vec p_1'=-E_1E_1'+|p_1||p_1'|cos\theta\]| 下面不带指标的p1代表三维模长 | p_1 |
带入到模方得到的方程中可以解出散射角θ1:
\[cos\theta_1=\frac{E_1'(E_1+m_2)-E_1m_2-m_1^2}{p_1p_1'}\] \[cos\theta_2=\frac{(E_1+m_2)(E_2'-m_2)}{p_1p_2'}\]双曲相对论解法
能量守恒和动量守恒写作
\[\left\{\begin{align} m_1cosh(s_1)+m_2cosh(s_2)=m_1cosh(s_3)+m_2cosh(s_4)\\ m_1sinh(s_1)+m_2sinh(s_2)=m_1sinh(s_3)+m_2sinh(s_4) \end{align}\right.\]两式相加
\[m_1e^{s_1}+m_2e^{s_2}=m_1e^{s_3}+m_2e^{s_4}\]1式平方-2式平方
\[m_1^2(cosh^2(s_1)-sinh^2(s_1))+m_2^2(cosh^2(s_2)-sinh^2(s_2))\\ +2m_1m_2(cosh(s_1)cosh(s_2)-sinh(s_1)sinh(s_2))\\ =m_1^2(cosh^2(s_3)-sinh^2(s_3))+m_2^2(cosh^2(s_4)-sinh^2(s_4))\\ +2m_1m_2(cosh(s_3)cosh(s_3)-sinh(s_4)sinh(s_4))\]利用$cosh^2x-sinh^2x=1$和$cosh(x-y)=coshxcoshy-sinhxsinhy$
\[cosh(s_1-s_2)=cosh(s_3-s_4)\]有两组解
\[\left\{\begin{align} s_1-s_2=s_3-s_4\\ s_1-s_2=s_4-s_3 \end{align}\right.\]第一组解代表碰撞前后快的还是快的,慢的还是慢的,这不满足碰撞后条件,所以舍去;用第二组解来解出v1,v2,第一步就是先算出exps1,exps2
\[\frac{e^{s_1}}{e^{s_4}}=\frac{e^{s_2}}{e^{s_3}}=\frac{m_1e^{s_1}+m_2e^{s_2}}{m_1e^{s_4}+m_2e^{s_3}}=\frac{m_1e^{s_3}+m_2e^{s_4}}{m_1e^{s_4}+m_2e^{s_3}}\] \[exps_1=exps_4\frac{m_1e^{s_3}+m_2e^{s_4}}{m_1e^{s_4}+m_2e^{s_3}}\] \[exps_2=exps_3\frac{m_1e^{s_3}+m_2e^{s_4}}{m_1e^{s_4}+m_2e^{s_3}}\] \[v_1/c=\frac{exp(s1)-exp(-s1)}{exp(s1)+exp(-s1)}\] \[v_2/c=\frac{exp(s2)-exp(-s2)}{exp(s2)+exp(-s2)}\]下面考虑碰撞过程前后的动量状态:用带有p1动量的粒子m1轰击另一个粒子m2,变为动量分别为p1’和p2’的两个粒子(质量不发生交换不增不减);作出动量守恒三角形如图
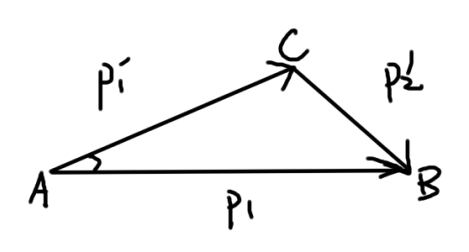
其中AB固定,求C的运动轨迹
和粒子分裂对比,他们都有一个初始固定的p,而后变为两个粒子;不同之处在于碰撞前是一个运动粒子和静止粒子,可以套结论知道这个轨迹就是椭圆,接下来求长短轴和偏心距离就好了。设碰撞前p方向为x轴(需要洛伦兹变换的主轴),那么质心速度
\[V=\frac{p_1}{E_1+m_2}\]在质心坐标系中碰后粒子动量大小相等长度相反
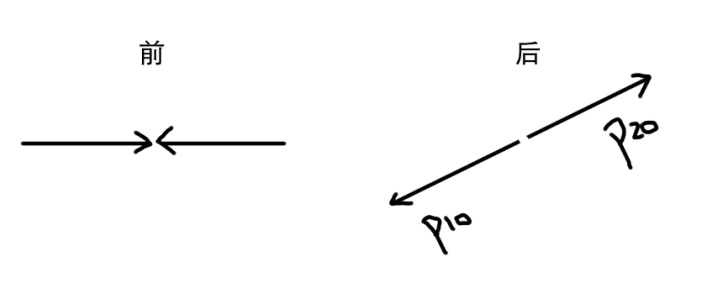
观察碰撞后两个坐标系下$p_{1i}p_2^i$守恒可以列出方程
\[-E_{10}E_{20}+p_{10}p_{20}=-E_1m_2\]| 其中,$ | p_{10} | = | p_{20} | = | p_0 | $且共线 |
从中解出p0^2
\[p_0^2=\frac{m_2^2(E_1^2-m_1^2)}{m_1^2+m_2^2+2m_2E_1}\]所以可以得到椭圆的半长短轴
\[p_0=\frac{m_2p_1}{\sqrt{m_1^2+m_2^2+2m_2E_1}}\] \[p_0\gamma=\frac{m_2p_1(E_1+m_2)}{m_1^2+m_2^2+2m_2E_1}\] \[\gamma=\frac{E_1+m_2}{\sqrt{m_1^2+m_2^2+2m_2E_1}}\]偏心距离
\[\frac12(p_1-p_0\gamma)\]将上面的式子带入即可(有点长长的)
刚体
omega哪有w好打?全部写成w了
前言:对于三维空间中一个给定形状的刚体(位置,转角未知),他的位形空间有几维?是什么样的?
为了确定朝向,需要用到SO(3)中的元素(也可以用SU(2))
为了确定位置,需要用到R^3中的元素
位置和朝向互相独立,所以使用直积,也就是说他的位形空间同构于R^3 x SO(3);当不考虑平移变化时,位形空间同构于SO(3)
更进一步的,SO(2)与复数一一对应,SO(3)与四元数一一对应,所以也可以用四元数来描述旋转
角动量,动能与w向量的变换关系
几个定义式:
\[\vec v=\vec w\times\vec r\] \[\vec J=\vec r\times\vec p=m(\vec r\times(\vec w\times\vec r))\]把J去掉m的部分展开一下
\[\vec w\times\vec r=\varepsilon^{ijk}w_ix_j\] \[\vec r\times(\vec w\times\vec r)=\varepsilon^{ijk}x_i\varepsilon_{lmj}w^lx^m=\varepsilon^{ijk}\varepsilon_{lmj}x_ix^mw^l\]下面观察两个epsilon,ik和lm分组铺满了除去j以外的两个指标位,所以要么(按顺序)ik=lm,要么ik=ml
第一种情况下,$\varepsilon^{ijk}\varepsilon_{lmj}=\varepsilon^{ijk}\varepsilon_{ikj}=-1$,$\varepsilon^{ijk}\varepsilon_{lmj}x_ix^mw^l=-x^kx_iw^i$最后一个等号后面的不是抽象指标表达,其中i只能取与k互异的两个值
第二种情况下,$\varepsilon^{ijk}\varepsilon_{lmj}=\varepsilon^{ijk}\varepsilon_{kij}=1$,$\varepsilon^{ijk}\varepsilon_{lmj}x_ix^mw^l=w^k(x_a^2+x_b^2)$最后一个等号后面的不是抽象指标表达,而是具体的平方,其中a和b是与k互异的分量
举个例子现在考虑Jx,角动量的第一个分量,令k=1:
\[J_x=m[(y^2+z^2)w_1-xyw_2-xzw_3]\]其他分类均是这种形式,可以看出J的每一个分量都可以用w作为基,再乘上与速度无关的量来表述
不妨把这种关系写成矩阵形式
\[\vec J =\begin{pmatrix} m(y^2+z^2)&-mxy&-mxz\\ -myx&m(x^2+z^2)&-myz\\ -mzx&-mzy&m(x^2+y^2) \end{pmatrix} \vec w\]不知道你们看着什么感觉,博主第一次看到这个觉得涩爆了。。
再次整理一下可以写作指标形式
\[I_{ik}=m(x_jx^j\delta_{ik}-x_jx_k)\]所以这个矩阵称作惯量张量I,角动量写作$J^i=I_j^iw^j$,当惯量张量I退化到单位矩阵的某个正数a倍的时候,J=aw且J与w同向
下面再算一下动能
\[E=\frac{1}{2}mv^2=\frac{m}{2}(\vec w\times\vec r)·(\vec w\times\vec r)\] \[(\vec w\times\vec r)·(\vec w\times\vec r)=\varepsilon^{ijk}w_ix_j\varepsilon_{lmk}w^lx^m=\varepsilon^{ijk}\varepsilon_{lmk}w_iw^lx_jx^m\]还是像上面一样分类,第一种情况ij=lm,此时$\varepsilon^{ijk}\varepsilon_{lmk}w_iw^lx_jx^m=w_a^2x_b^2+w_b^2x_a^2$老规矩等式右边不是指标表示,2是平方,ab是与k互异的另两个指标
第二种情况ij=ml,此时$\varepsilon^{ijk}\varepsilon_{lmk}w_iw^lx_jx^m=-2w_aw_bx_ax_b$,等式右边不是指标表示
举个例子计算k=1的项,他们是$w_2^2z^2+w_3^2y^2-2w_2w_3yz$,所有分量均是这个形式
由于能量只用考虑加和后的标量,所以我们可以随便移动加法的顺序并分组;对于每个w_i^2,他都与和i不同的两个x_j^2乘加了两次;所有交叉项都存在且有一个2的系数。在考虑到上面的惯性张量,可以写作二次型的形式
\[E =\frac{1}{2}\vec w^T\begin{pmatrix} m(y^2+z^2)&-mxy&-mxz\\ -myx&m(x^2+z^2)&-myz\\ -mzx&-mzy&m(x^2+y^2) \end{pmatrix} \vec w\]除了用外积的指标形式展开以外,还可以使用混合积的交换律a·(bxc)=b·(cxa)=c·(axb)
\[m\vec v·(\vec w\times\vec r)=m\vec w·(\vec r\times\vec v)=\vec w·(\vec r\times\vec p)=\vec w^TI\vec w\]移轴定理(是叫这个名字吗)朗道p103
总质量是$\mu$,原本的惯量张量是I_ik,将原点平移a^i(平移距离记作a)后的惯量张量
\[I_{ik}'=I_{ik}+\mu(a^2\delta_{ik}-a_ia_k)\]惯量主轴(惯量张量对角化)
我们知道一个正定实对称矩阵一定可以对角化,并且其特征向量还是两两垂直的。这就意味着对于一个物体,一定存在一个特殊的(绑在他身上的)三维笛卡尔坐标系,使得惯量张量在这个坐标系下简化为对角阵的形式(I=diag(I_1,I_2,I_3))。那么就叫这个特殊的坐标系为惯量主轴。
进一步的,I1,I2,I3这三个特征值之间满足三角不等式,且仅在平面物体时取等
柯尼希定理(答应我,不要在写能量的时候使用非质心点了)
一个系统能量=质心平动能+轴过质心的转动能
重新认识三维角速度
本小节主要来自阿诺德和高显,本小节的$\vec v$若不加说明则默认速度的角向分量
首先由角速度与线速度的关系$\vec v=\vec w\times\vec r$,定义线性算子$A·=\vec w\times ·$,很明显算子A将R^3打到了R^3上,且具有反对称性。那么,能不能找到一个反对称矩阵B,使得B作用在三维矢量上和A的作用等效呢?答案是可以的。
引理(阿诺德p100):三维有向欧氏空间中的每一个反对称算子都是与某一固定矢量之矢量积(外积)
\[A\vec q=\vec w\times\vec q,~~\forall q\in R^3\]证:$R^3\to R^3$的所有反对称算子构成一个线性空间,由于反对称矩阵仅由主对角线下方3个元素决定,所以该线性空间的维数是3
另一方面,与固定矢量w作外积也是线性反对称算子,所以,所有的外积某一矢量w的外积的这些算子构成反对称算子空间的一个线性子空间
这个子空间的维数是3,与原始空间dim相等,所以外积张成的算子空间即为所有反对称算子张成空间
为了找到这个可以替代$\vec w\times$算子的矩阵到底长什么样,不妨把$\vec w\times\vec r$写出来
\[\vec w\times\vec r=\vec v=(w_2z-w_3y,w_3x-w_1z,w_1y-w_2x)\]凑成矩阵吧
\[\vec v =\begin{pmatrix} 0&-w_3&w_2\\ w_3&0&-w_1\\ -w_2&w_1&0 \end{pmatrix} \begin{pmatrix} x\\ y\\ z \end{pmatrix}\]所以定义角速度矩阵
\[\Omega_{ij}=\begin{pmatrix} 0&-w_3&w_2\\ w_3&0&-w_1\\ -w_2&w_1&0 \end{pmatrix}\]按理说,只要知道每个时刻质点所对角,就可以通过求导等操作求出角速度w。同样的,只要有旋转矩阵R(t),也可以求出角速度矩阵Ω
记实验室坐标系为{$\bar e_i$}为不随时间变化的常数,转动后的坐标系为{ei},转动矩阵为R,则有从实验室坐标系到转动后坐标系的变换关系:(矩阵指标位置的微小变化暗示了行列读书顺序,左侧是行指标,右侧是列指标)
\[e_i(t)=R_i^{~j}(t)\bar e_j~~;~~\bar e_j=R_{~j}^i(t)e_i\]上式对t求导,并把实验室坐标系代换掉
\[\dot e_i=\dot R_i^{~j}(t)\bar e_j=\dot R_i^{~j}(t)R_{~j}^k(t)e_k\]另一方面,速度还可以由$\vec v=\Omega\vec r$导出,即
\[\dot{e_i}=\Omega_i^{~j}e_j\]通过$\dot{e_i}$的搭桥,可以得到
\[\Omega_i^{~j}=\dot R_i^{~k}R_{~k}^j=-\dot R_i^{~k}R_{k}^{~j}\]矩阵形式写作
\[\Omega=-\dot RR=\dot RR^T\]由于主动观点被动观点的不同约定,Ω可能会相差一个负号
欧拉角
如何描述三维的旋转状态?首先可以确定的是有3个自由度。给出一种最朴素的下界表达方式(分支定界太多导致的):(以x为轴旋转角,以y轴旋转角,以z轴旋转角)这样一定可以描述所有三维空间中的旋转运动。玩过小绿人(坎巴拉太空计划)的人都知道,火箭在空中分为滚动-俯仰-偏航角,就是用到了3个不同轴旋转体系来描述的
那只用2个轴来进行旋转操作,但是分三次旋转,可以描述所有三维旋转状态吗?是可以的,这就是所谓的欧拉角
再激进一点,只用到一个轴,那你无论分多少次旋转都可以合并为一次旋转,自由度只有1,肯定是不够描述所有旋转的
现在给你一个三维直角坐标系,要转到一个特定的状态,按照欧拉角的方法分为三步走:
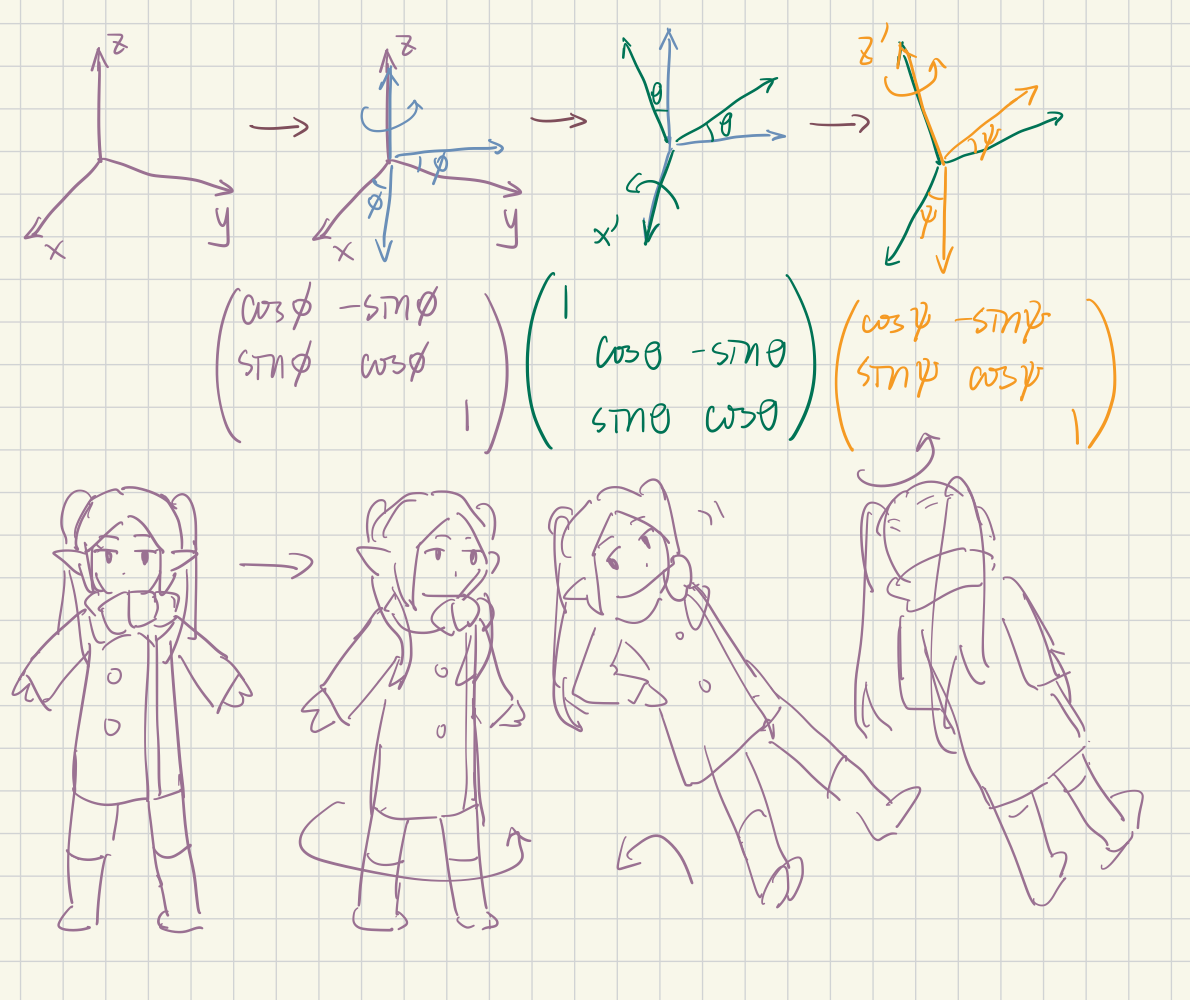
1.绕z轴(随物体旋转的坐标系)旋转φ
平面内旋转的矩阵都好写
\[R_3=\begin{pmatrix} cos\phi&-sin\phi&\\ sin\phi&cos\phi&\\ &&1 \end{pmatrix}\]2.绕x轴(随物体旋转的坐标系)旋转θ
\[R_2=\begin{pmatrix} 1&&\\ &cos\theta&-sin\theta\\ &sin\theta&cos\theta\\ \end{pmatrix}\]1.绕z轴(随物体旋转的坐标系)旋转ψ
\[R_1=\begin{pmatrix} cos\psi&-sin\psi&\\ sin\psi&cos\psi&\\ &&1 \end{pmatrix}\]由于首尾两次绕z轴旋转矩阵的形式完全一致,所以在3个角度均不确定的情况下正着乘(从左到右)或者从右到左都是一样的(但是如果对确定的φ!=ψ,就不能随便这么玩了)
下面看看乘起来之后长什么样
\[R_3R_2R_1=\begin{pmatrix} cos\psi cos\phi-cos\theta sin\phi sin\psi&sin\phi cos\psi+cos\theta sin\psi cos\phi&sin\theta sin\psi\\ -cos\phi sin\psi-cos\theta sin\phi cos\psi&-sin\phi sin\psi+cos\theta cos\psi cos\phi&sin\theta cos\psi\\ sin\theta sin\phi&-sin\theta cos\phi&cos\theta\\ \end{pmatrix}\]这个就是所谓的转动矩阵$R(\phi,\theta,\psi)$,再根据转动矩阵与角速度矩阵Ω的关系,得到如下方程
\[\Omega=\dot R R=\begin{pmatrix} 0&-w_3&w_2\\ w_3&0&-w_1\\ -w_2&w_1&0 \end{pmatrix}\]可以把角速度$\vec w$的各个分量用欧拉角来表示出来(这也太难解了)
\[\left\{\begin{align} w_1=sin\theta sin\psi\dot\phi+cos\psi\dot\theta\\ w_2=sin\theta cos\psi\dot\phi-sin\psi\dot\theta\\ w_3=cos\theta\dot\phi+\dot\psi \end{align}\right.\]如果不想用转动矩阵求导的话,还可以将坐标变化后的坐标与原坐标的线性关系写出来,代入$\vec w=\dot\phi e_3’’+\dot\theta e_1’+\dot\psi e_3$(几个撇代表转了第几步),虽然数学上可能看起来简单一些,但这需要结合图进行更多物理层面的推导。
欧拉动力学方程
有了角速度w的坐标表示(欧拉角)之后,理论上来说可以代入欧拉-拉格朗日方程甚至是哈密顿正则方程来解3个分量的运动学方程了,相当于用欧拉角参数走个过场,最后还是回到了w之间的关系上,这是强坐标依赖的。(这部分待更新)
下面用不那么坐标依赖的方式来写欧拉动力学方程
| 在三维角速度那一节讨论过只有角向速度(<=> | r | 不变)的基矢的速度可以写作$\vec v=\vec w\times\vec r$,那么如何把这种表示速度的方式推广到既有角向速度又有径向速度的矢量上呢?由于角向与径向的正交性,只需要再加上径向速度即可,写作 |
其中,d*/dt代表只对坐标分量求导的意思(来自宋浩老师的约定)
分量形式写作
\[\frac{DX^i}{dt}=\partial_t X^i+\Gamma_{tj}^iX^j\]这是我自己仿造微分几何凑出来的,甚至还可以算联络$\Gamma_{tj}^i=\begin{pmatrix}
0&-w_3&w_2
w_3&0&-w_1
-w_2&w_1&0
\end{pmatrix}$(i是行指标j是列指标)
既然X是任意的矢量的话,角动量J当然也适用。选取惯量主轴,设M是力矩,则由角动量定理得
\[\dot{\vec J}=\frac{d^*}{dt}\vec J+\vec w\times\vec J=\vec M\]在惯量主轴上J写作
\[\vec J=(I_1w_1,I_2w_2,I_3w_3)\]则
\[\vec w\times\vec J=(w_2w_3(I_3-I_2),w_1w_3(I_1-I_3),w_1w_2(I_2-I_1))\] \[\frac{d^*}{dt}\vec J=(I_1\dot w_1,I_2\dot w_2,I_3\dot w_3)\]欧拉动力学方程的分量形式写作
\[\left\{\begin{align} I_1\dot w_1+w_2w_3(I_3-I_2)=M_1\\ I_2\dot w_2+w_1w_3(I_1-I_3)=M_2\\ I_3\dot w_3+w_1w_2(I_2-I_1)=M_3 \end{align}\right.\]当没有外力矩时,方程组回到自由形式
小振动
这一章提不起多大兴趣,就随便抄抄当占位算了
注:本文中会出现$\lambda_{12}=\pm ai$的情况,由于这个正负不影响简谐解,所以可能合写为$\lambda_1=ai$
振动方程与解
都是玩烂了的,只是放到一起总结而已,没有新东西,那就再自己推一遍(注:通解写sin还是cos无所谓,我就乱写了)
简谐运动
\[\ddot x+w_0^2x=0\]解
\[x=Asin(w_0t+\varphi_0)\]
阻尼振动
\[\ddot x+2\beta\dot x+w_0^2x=0\]解
\[x=Ae^{-\beta t}sin(\sqrt{w_0^2-\beta^2}t+\varphi_0)\]
(常见)欠阻尼$ \beta < w_0 $,此时特征根$\lambda_{12}=-\beta\pm\sqrt{w_0^2-\beta^2}i$ \[x=(At+B)e^{-\beta t}\]
临界阻尼$ \beta = w_0 $,此时特征根$\lambda_{12}=-\beta$ \[x=Ae^{-\beta+\sqrt{\beta^2-w_0^2}}+Be^{-\beta-\sqrt{\beta^2-w_0^2}}\]
过阻尼$ \beta > w_0 $,此时特征根$\lambda_{12}=-\beta\pm\sqrt{\beta^2-w_0^2}$
受迫振动
\[\ddot x+w_0^2x=F_0coswt\]齐次通解
\[x=Acos(w_0t+\varphi_0)\]当驱动频率不等于固有频率时,非齐次特解
\[x=\frac{F_0}{w_0^2-w^2}coswt\]所以该条件下的非齐次解为
\[x=\frac{F_0}{w_0^2-w^2}coswt+Acos(w_0t+\varphi_0)\]下面讨论驱动力频率与固有频率相等的情况,此时特解为
\[x=\frac{F_0}{2w_0}tsinw_0t\]非齐次解为
\[x=\frac{F_0}{2w_0}tsinw_0t+Asin(w_0t+\varphi_0)\]当t足够大时,第一项占主导,此时可以近似认为振动相位落后外力相位$\pi/2$,并且随着t的增大发散
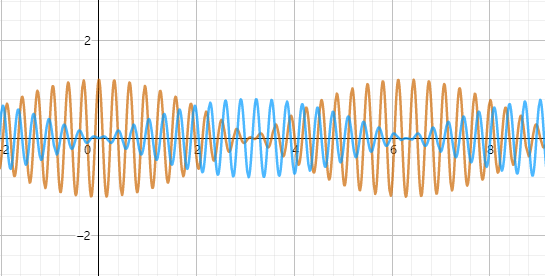
驱动力与固有频率很靠近产生拍
由于w不等于w0,所以(w-w0)t=φ一定有解,这意味着无论最初驱动力与固有振动相位相差多少,总存在一个时刻使得两者没有相位差。(为了证明方便)从该点开始计时,此时表达式中无额外相位差
不妨设$w=\bar w-\varepsilon$,$w_0=\bar w+\varepsilon$,其中ε是一个小数字
则$\frac{F_0}{w_0^2-w^2}=\frac{F_0}{4\varepsilon\bar w}$,这是一个足够大的数,将x写作
\[x=\frac{F_0}{4\varepsilon\bar w}cos((\bar w-\varepsilon)t)+Acos((\bar w+\varepsilon)t)\]整理一下,把前两个cos打开可以相互消一下
\[x=(\frac{F_0}{4\varepsilon\bar w}+A)cos\varepsilon tcos\bar wt+(\frac{F_0}{4\varepsilon\bar w}-A)sin\bar wtsin\varepsilon t\]相当于相位相差$\pi/2$的两束驻波的叠加
受迫阻尼振动
\[\ddot x+2\beta \dot x+w_0^2x=F_0coswt\]
为了简单,只考虑出现最多的欠阻尼情况,此时$ \beta < w_0 $,特征根$\lambda_{12}=-\beta\pm\sqrt{w_0^2-\beta^2}i$ 齐次通解
\[x=Ae^{-\beta t}sin(\sqrt{w_0^2-\beta^2}t+\varphi_0)\]设该系统的固有频率$w_1=\sqrt{w_0^2-\beta^2}$
当驱动频率不等于w1时,找一个特解(搞个Acoswt+Bsinwt然后一顿乱代)
\[x=\frac{F_0(w_0^2-w^2)}{(w_0^2-w^2)^2+4\beta^2w^2}coswt+\frac{2F_0\beta w}{(w_0^2-w^2)^2+4\beta^2w^2}sinwt\]合起来得到通解
\[x=\frac{F_0(w_0^2-w^2)}{(w_0^2-w^2)^2+4\beta^2w^2}coswt+\frac{2F_0\beta w}{(w_0^2-w^2)^2+4\beta^2w^2}sinwt\\+Ae^{-\beta t}sin(\sqrt{w_0^2-\beta^2}t+\varphi_0)\]可以看出,最后一项(齐次项)随着时间推移逐渐减少趋于0,所以关注特解项:
相移:将前两项利用辅助角公式合并为一项
\[\frac{F_0(w_0^2-w^2)}{(w_0^2-w^2)^2+4\beta^2w^2}coswt+\frac{2F_0\beta w}{(w_0^2-w^2)^2+4\beta^2w^2}sinwt\\ =F_1cos(wt-\varphi)\]其中
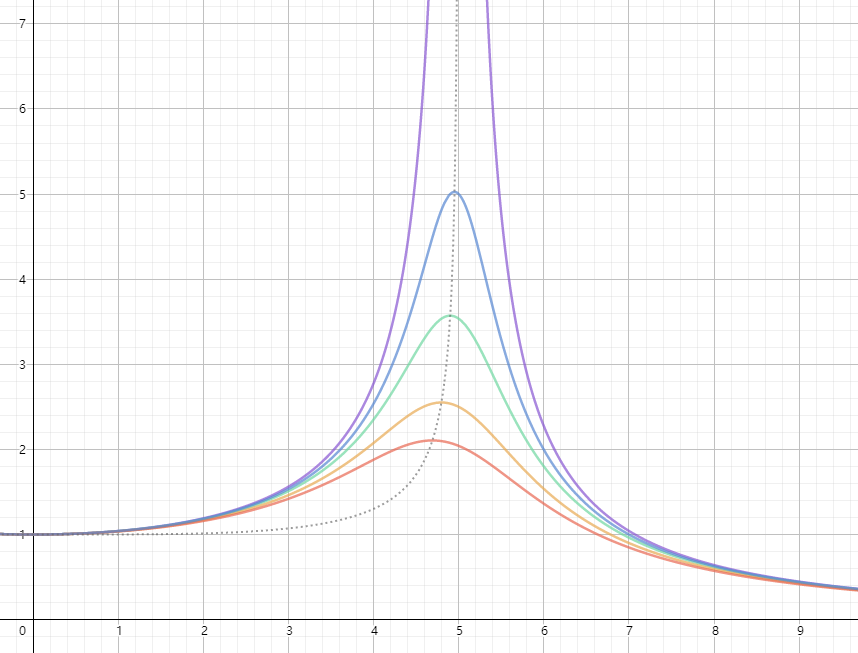
\[F_1=\frac{F_0}{\sqrt{(w_0^2-w^2)^2+4\beta^2w^2}}\] \[tan\varphi=\frac{2\beta w}{w_0^2-w^2}\]也就是说,当驱动频率比(0阻尼的)固有频率w0小时,受迫振动项会较驱动有0~$\pi/2$的小延迟;当驱动频率比(0阻尼的)固有频率w0大时,受迫振动项会较驱动有$\pi/2$~$\pi$的大延迟;当驱动频率=w0时,cos项没了,受迫振动项恰延迟$\pi/2$
下面关注振幅分母
\[(w_0^2-w^2)^2+4\beta^2w^2=w^4+(4\beta^2-2w_0^2)w^2+w_0^4\\ =[w^4+(4\beta^2-2w_0^2)w^2+(2\beta^2-w_0^2)^2]-(2\beta^2-w_0^2)^2+w_0^4\\ =(w^2-(w_0^2-2\beta^2))^2+4\beta^2(w_0^2-\beta^2)\](还可以看到,后面的$w_0^2-\beta^2$是阻尼系统固有频率w1^2)
当$w=\sqrt{w_0^2-2\beta^2}$时,振幅F1取最大值
\[F_{1max}=\frac{F_0}{2\beta w_1}\]也可以用w写作
\[F_{1max}(w)=\frac{F_0}{\sqrt{(w_0^2-w^2)(w_0+w^2)}}\]
级数展开-振动方程导出
在已知势能V(r)最低点r_0附近的小振动:
第一种解法:对V(r_0+r)差分泰勒展开
\[V(r_0+r)-V(r_0)=\frac{V''(r_0)}{2}r^2+O(r^2)\]在附近小振动时的L
\[L=\frac{m}{2}\dot r^2-\frac{V''(r_0)}{2}r^2\]利用欧拉拉格朗日方程
\[m\ddot r=-V''(r_0)r\]第二种方法分析回复力,最后也是得到上面这个振动方程
下面直接对拉氏量差分作微扰
\[L(t,q+\delta q,\dot q+\delta\dot q)-L(t,q,\dot q)=\sum_{n=0}^\infty(\delta q\frac{\partial}{\partial q}+\delta\dot q\frac{\partial}{\partial\dot q})^nL(t,q,\dot q)-L(t,q,\dot q)\]和先前的势能最低点展开有异曲同工之妙,0阶1阶全没有,只有二阶项
\[\Delta L=\frac{\partial^2L}{\partial q^2}\delta q^2+\frac{2\partial^2L}{\partial q\partial\dot q}\delta q\delta\dot q+\frac{\partial^2}{\partial\dot q^2}\delta\dot q^2\]最小作用量原理仍然需要满足ΔL取极值,也即
\[\delta\int\Delta Ldt=\delta\int dt[(\frac{\partial^2L}{\partial q^2}\delta q^2-\frac{d}{dt}\frac{\partial^2L}{\partial q\partial\dot q})\delta q^2+\frac{\partial^2L}{\partial\dot q^2}\delta\dot q^2]=0\]这就是一维扰动通用的作用量方程,下面看看(非耦合的?简单的?)机械系统中能得到什么样的方程
\[L=T(\dot q)-V(q)\] \[\frac{\partial^2L}{\partial q^2}=-V''(q)~~~\frac{\partial^2L}{\partial q\partial\dot q}=0~~~\frac{\partial^2L}{\partial\dot q^2}=T''(\dot q)\] \[-T''\ddot q-V''q=0\Rightarrow\ddot q+(V''/T'')q=0\]该系统的固有频率为$\sqrt{V’‘/T’’}$
进一步,当$T=\frac{m}{2}\dot q^2$时,T’‘=m,代入可得
\[\ddot q+(V''/m)q=0\]回到了一开始推出来的特殊形式
简正模式/弱耦合
考虑这样的模型
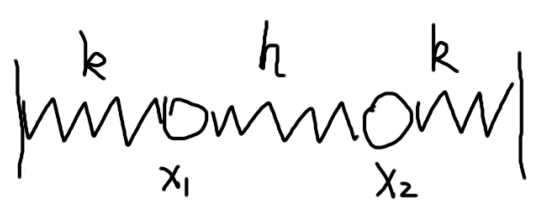
两个小球质量都是m,两端弹簧劲度系数为k,中间劲度系数为h,两个墙壁所夹长度恰为三个弹簧原长和,求运动解
不管是先写L还是受力分析,以平衡位置为原点,可以得出这样的方程
\[\left\{\begin{align} m\ddot x_1+(k+h)x_1-hx_2=0 \\ m\ddot x_2+(k+h)x_2-hx_1=0 \end{align}\right.\]第一种方法:线代启动
\[\frac{d^2}{dt^2}\begin{pmatrix} x_1\\ x_2 \end{pmatrix} =\begin{pmatrix} -(k+h)/m & h/m\\ h/m & -(k+h)/m \end{pmatrix}\begin{pmatrix} x_1\\ x_2 \end{pmatrix}\]看上去解就是$\vec x=C_1exp(\sqrt{A}t)+C_2exp(-\sqrt{A}t)$,但是这太抽象了点
还是和一维一样用本征方程
\[\begin{vmatrix} -(k+h)/m-\lambda^2 & h/m\\ h/m & -(k+h)/m-\lambda^2 \end{vmatrix}=0\]解得
\[\lambda_1=\sqrt{\frac{k+2h}{m}}i~~~\lambda_2=\sqrt{\frac{k}{m}}i\]λ1所对应的特征向量为$\begin{pmatrix}
1
-1
\end{pmatrix}$,λ2所对应的特征向量为$\begin{pmatrix}
1
1
\end{pmatrix}$
代回可得到解
\[\begin{pmatrix} x_1\\ x_2 \end{pmatrix}=A\begin{pmatrix} 1\\ -1 \end{pmatrix}expi\sqrt{\frac{k+2h}{m}}t+B\begin{pmatrix} 1\\ 1 \end{pmatrix}expi\sqrt{\frac{k}{m}}t\\ =A\begin{pmatrix} 1\\ -1 \end{pmatrix}cos(\sqrt{\frac{k+2h}{m}}t+\varphi_A)+B\begin{pmatrix} 1\\ 1 \end{pmatrix}cos(\sqrt{\frac{k}{m}}t+\varphi_B)\]称$\sqrt{\frac{k+2h}{m}}$为快频率wf,$\sqrt{\frac{k}{m}}$为慢频率ws;这个解代表系统由{2质点同向运动}与{2质点相向运动}这两个简正模式组成
至于另一种处理方法,就是坐标代换,总之最后也是得到两个简正模式,我觉得真不如线性代数
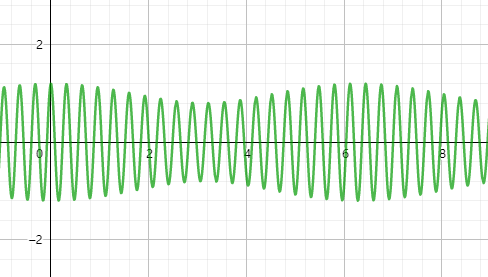
弱耦合的拍:
当h(两质点相互作用力)远小于k时,一定可以通过泰勒展开将这两个频率写作
\[w_f=\bar w+\varepsilon~~~w_s=\bar w-\varepsilon\]剩下的处理方法参考本章第一节,总之这个情况下的解是
\[\begin{pmatrix} x_1\\ x_2 \end{pmatrix}=(A\begin{pmatrix} 1\\ -1 \end{pmatrix}+B\begin{pmatrix} 1\\ 1 \end{pmatrix})cos\varepsilon tcos\bar w+(A\begin{pmatrix} -1\\ 1 \end{pmatrix}+B\begin{pmatrix} 1\\ 1 \end{pmatrix})sin\varepsilon tsin\bar{w}\]这是先前讨论过的拍的合成形式
阻尼二维震荡
\[m\frac{d^2}{dt^2}\begin{pmatrix} x_1\\ x_2 \end{pmatrix} =\begin{pmatrix} -k-K & K\\ K & -k-K \end{pmatrix}\begin{pmatrix} x_1\\ x_2 \end{pmatrix}-b\frac{d}{dt}\begin{pmatrix} x_1\\ x_2 \end{pmatrix}\]前略,特征方程根为
\[\lambda_{12}=\frac{-b\pm\sqrt{b^2-4m(k+2K)}}{2m}\] \[\lambda_{34}=\frac{-b\pm\sqrt{b^2-4mk}}{2m}\]一般情况下只讨论弱阻尼情况
滚筒荡秋千
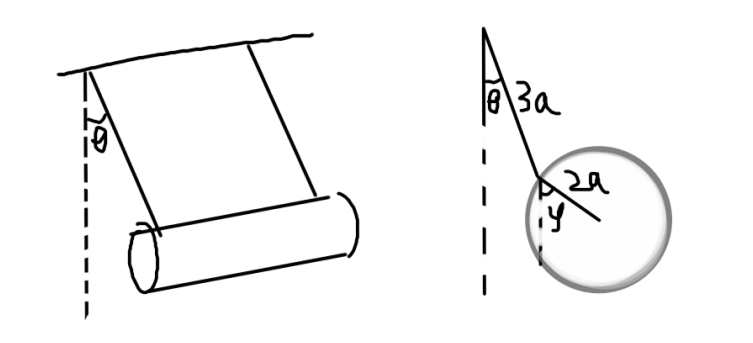
注意看,这个滚筒是个空心的,就像上厕所的时候用的厕纸一样;然后θ和φ都很小(这个世界一切为了做题而生!x)
先写动能,找到质心平动能和转动能就好了
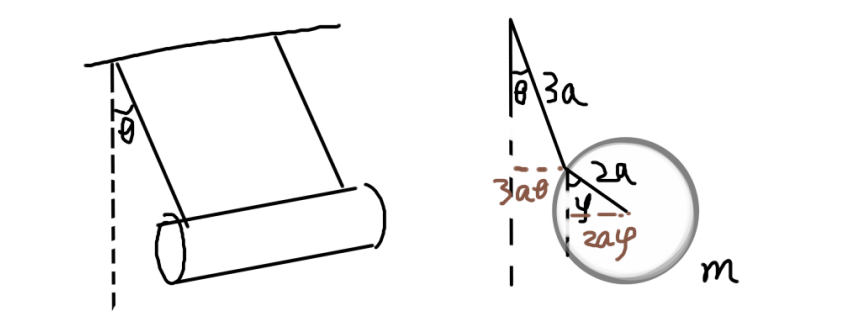
利用微妙的小量近似,圆筒质心水平方向位移为3aθ+2aφ,竖直位移看作0,所以
\[T_平=\frac{m}{2}(3a\dot\theta+2a\dot\varphi)^2\]转动能仅由φ坐标控制,并且圆筒的转动惯量=m(2a)^2
\[T_转=\frac{1}{2}\dot\varphi^2({m(2a)^2})\]加起来打开
\[T=\frac{m}{2}(9a^2\dot\theta^2+12a^2\dot\theta\dot\varphi+8a^2\dot\varphi^2)\]然后势能很好写,就跟你写双摆势能一样
\[V=mg(-3acos\theta-2acos\varphi)\]利用$cosx=1-\frac{x^2}{2}$近似写作
\[V=mg(-3a+\frac{3}{2}a\theta^2-2a+\frac{2}{2}a\varphi^2)\]由于0势能点的任意性,常数项统统扔掉不要
\[V=\frac{mg}{2}(3a\theta^2+2a\varphi^2)\]拉格朗日量
\[L=T-V=\frac{m}{2}(9a^2\dot\theta^2+12a^2\dot\theta\dot\varphi+8a^2\dot\varphi^2)-\frac{mg}{2}(3a\theta^2+2a\varphi^2)\]用欧拉拉格朗日方程写运动方程,自己算,我就直接放结果了
\[\left\{\begin{align} ma^2(9\ddot\theta+6\ddot\varphi)=-3mga\theta \\ ma^2(6\ddot\theta+8\ddot\varphi)=-2mga\varphi \end{align}\right.\]初步处理一下
\[\left\{\begin{align} 3\ddot\theta+2\ddot\varphi=-\frac{g}{a}\theta \\ 3\ddot\theta+4\ddot\varphi=-\frac{g}{a}\varphi \end{align}\right.\]改写成矩阵
\[\begin{pmatrix} 3 & 2\\ 3 & 4 \end{pmatrix}\frac{d^2}{dt^2}\begin{pmatrix} \theta\\ \varphi \end{pmatrix} =-\frac{g}{a}\begin{pmatrix} \theta\\ \varphi \end{pmatrix}\]把左边那个矩阵逆过去
\[-\frac{a}{g}\frac{d^2}{dt^2}\begin{pmatrix} \theta\\ \varphi \end{pmatrix} =\begin{pmatrix} \frac{2}{3} & -\frac{1}{3}\\ -\frac{1}{2} & \frac{1}{2} \end{pmatrix}\begin{pmatrix} \theta\\ \varphi \end{pmatrix}\]解特征方程,这次设$\ddot\theta=-w^2\theta$,设$\frac{a}{g}w^2=\lambda$(就是要丢到等式右边的东西)得到
\[\lambda^2-\frac{7}{6}\lambda^2+\frac{1}{6}=0\]解得
\[\lambda=1~or~\frac{1}{6}\]得到两种角速度
\[w_f=\sqrt\frac{g}{a}~~w_s=\sqrt{\frac{g}{6a}}\]对应的特征向量
\[\begin{pmatrix} \theta\\ \varphi \end{pmatrix}_f=\begin{pmatrix} 1\\ -1 \end{pmatrix}~~\begin{pmatrix} \theta\\ \varphi \end{pmatrix}_s=\begin{pmatrix} 2\\ 3 \end{pmatrix}\]说实话博主并不能直观的看出这两种振动模式是为啥,还是那个弹簧振子的两个减震模容易理解一些
放在一起得到最后的解
\[\begin{pmatrix} \theta\\ \varphi \end{pmatrix}=A\begin{pmatrix} 1\\ -1 \end{pmatrix}cos(\sqrt\frac{g}{a}t+\varphi_A)+B\begin{pmatrix} 2\\ 3 \end{pmatrix}cos(\sqrt{\frac{g}{6a}}t+\varphi_B)\]就这样,当你看到这条的时候,我应该已经考完啦!
原创文章转载请注明出处: 理论力学二