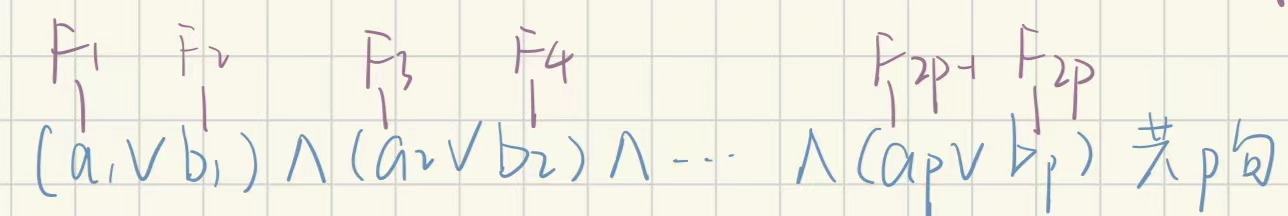新手产生的图论入门级代码堆以及相关性质证明

新手产生的图论入门级代码堆以及相关性质证明

经典P与NP问题

P问题：多项式时间复杂度内能判断是否有解

例：欧拉路径（七桥问题）

import copy

Graph = [[0,1,0,0,0,1],
         [1,0,1,1,1,0],
         [0,1,0,0,1,0],
         [0,1,0,0,2,1],
         [0,1,1,2,0,0],
         [1,0,0,1,0,0]]

Road = []

def CheckPath(G):#检查是否存在欧拉路径，有欧拉回路返回0，有欧拉路径返回[n,m]两个端点，啥都无就返回-1
    OddCount = 0
    EvenCount = 0
    odd = []
    numcount = 0
    for i in G:
        hand = 0
        for j in i:
            hand +=j
        if hand%2==0:
            EvenCount+=1
        elif hand%2==1:
            OddCount+=1
            odd += [numcount]
        numcount += 1
    if OddCount==0:
        return 0
    elif OddCount == 2:
        return odd
    else:
        return -1

def ConnectionPoint(G,n):#检查图中n可以连接多少点，方法：从已连接的点集出发搜索，共搜索顶点-1轮
    Points = [n]
    for i in range(0,len(G)-1):#i代表搜索轮数
        for j in Points:#j代表出发点
            for k in range(0,len(G)):#k代表待定终点
                if G[j][k]!=0 and k not in Points:
                    Points += [k]
    return len(Points)

def CheckBridge(G,n,m):#检查n与m之间的路是否是现有图G的桥，是桥返回1，非桥返回0
    if G[n][m]>=2:#有多条路，必非桥
        return 0
    else:
        G2 = copy.deepcopy(G)
        G2[n][m]=G2[m][n]=0
        if ConnectionPoint(G,n) == ConnectionPoint(G2,n):
            return 0
        else:
            return 1


def FindPath(G,rd):#每调用一次就给出当前的下一步,并删去已走过的路径
    G = copy.deepcopy(G)
    briPoint = []
    unbriPoint = []
    for i in range(0,len(G)):
        if G[rd[-1]][i] != 0:
            if CheckBridge(G,rd[-1],i) == 1:
                briPoint += [i]
            else:
                unbriPoint+=[i]
    if briPoint == unbriPoint == []:
        return rd
    elif unbriPoint == []:#被迫只能走桥
        G[rd[-1]][briPoint[0]]=G[briPoint[0]][rd[-1]]=0
        rd += [briPoint[0]]
        return FindPath(G,rd)
    else:#优先走非桥
        G[rd[-1]][unbriPoint[0]] -=1
        G[unbriPoint[0]][rd[-1]] -=1
        rd += [unbriPoint[0]]
        return FindPath(G, rd)

if ConnectionPoint(Graph,0)==len(Graph):
    Ps = CheckPath(Graph)
    if Ps == 0:
        print('存在欧拉回路')
        i = 1
        while Graph[0][i]!=0:
            i +=1
        Graph[0][i-1]-=1
        Graph[i-1][0] -= 1
        print(FindPath(Graph, [0])+[0])
    elif Ps == -1:
        print('不存在欧拉回路或欧拉路径')
    else:
        print('存在欧拉路径')
        print(FindPath(Graph,[Ps[0]]))
else:
    print('图不连通')

NP问题：多项式时间内可判断解是否可行的问题

例如旅行商问题：不重复地走完所有顶点，也称作寻找哈密顿路径

寻找哈密顿环最坏的方法是暴力搜索（列举所有点的排列）然后判定是否可行（相邻点之间均有路）

利用判定函数给出的寻找方案：每次删除一条边，查询是否还存在哈密顿环

只要P!=NP这个大前提存在，那么判断一个图是否有哈密顿环就不可能在多项式时间内完成

欧拉回路：遍历所有边的回路

欧拉路径：遍历所有边的路径（一笔画问题）

已知：每个顶点度是偶数<=>连通图存在欧拉回路

习题：连通图存在欧拉路径<=>只有两个顶点的度是奇数

充分性：欧拉路径的首位对应奇数度，中间经过的点，每经过一次使用掉该点的两个度，所以中间的点一定是偶数度，也即该图只有两个顶点的度是奇数

必要性：将这两个奇数度点相连，形成一个每个顶点度是偶数的图，那么他一定存在欧拉回路；将这个欧拉回路去掉刚刚加的边，就是该图的欧拉路径了

图与邻接矩阵

定义在无向简单图上的拉普拉斯矩阵：度矩阵（对角阵）-邻接阵

大概长这个样子

\[L =\begin{pmatrix} 2&-1&-1\\ -1&1&0\\ -1&0&1\\ \end{pmatrix}\]

实对称矩阵，有边的地方填上-1，对角填该顶点的度（有多少只手）；拉普拉斯矩阵满足每行/列和为0，所以不满秩；且由于是实对称矩阵，所以可以对角化；综上，必然有一个特征值是0，其对应的特征向量是(1,1,…,1)

拉普拉斯阵的性质：

\[\vec x^TL\vec x=\sum_{ij\in E}(x_i-x_j)^2\Rightarrow L~~positive~~semi-definite\]

就是说L半正定，数学环境下不想打汉字怕出麻烦；二次型就等于边所对应分量差的平方，再对所有边求和。证明左侧是简单的：每个$(x_i-x_j)^2$包含$x_i^2$、$-2x_ix_j$、$x_j^2$(废话，兄弟)，求和之后正好平方项有度个，交叉项对应L中在含边处填上的-1，刚好相等

再来一个性质：

图不联通<=>L中次小特征值为0

引理：次小特征值α的另一种表述：$α=\min_{\sum x_i=0~and~||x||_2=1}x^TLx$（分量和为0是为了与(1,1,…,1)垂直，2范数为1是归一）

充分性（构造x性证明）：图不连通，则L经过行或列的顺序交换（或图编号的更换），可化为分块对角阵（这句话好像对证明没啥帮助）设图（n个顶点）割裂的一部分为含a个顶点的A，和n-a个顶点的B（A和B本身不要求联通，只要求A与B之间没有桥）

下面分A区B区给x赋值：$\forall i \in A_{vertex},x_i=\sqrt{\frac{n-k}{nk}};\forall j \in B_{vertex},x_j=-\sqrt{\frac{k}{n(n-k)}}$

事实上这就是事先想好同块同值，然后解引理中min下限制条件方程组拿到的

代入到二次型中：$x^TLx=\sum_{ij\in E}(x_i-x_j)^2=\sum_{ij\in A}(x_i-x_j)^2+\sum_{ij\in B}(x_i-x_j)^2$

又因为每块x分量值一样，所以上式的结果为0；因为半正定，所以这就是我们找的α，充分性得证

必要性：把取到极小值0时的x拿出来，再次观察限制条件$\sum x_i=0~and~||x||_2=1$，这意味着x非0向量，且x分量非全部一样

取出第一个非零分量$x_k$，并将所有值等于$x_k$的分量对应的顶点取出来，沿用原图G的边（能不删就不删），组成子图A（如果A与G-A有连接，则两个端点对应的分量值不同！）

要使平方和为0，则必有每项均为0，也即$\forall ~ij \in~G_{edges},x_i=x_j$,这与上面一段话括号中内容矛盾，也就是说A与G-A不连通。而x分量非全部一样保证了A是真子图，必要性得证。

再来一个性质：

L中0的特征重数=图中连通分支的个数

这是自证明请自行甄别可行性

这个证明就要用到：图不连通，则L经过行或列的顺序交换（或图编号的更换），可化为分块对角阵。而每个连通分支对应一个小的矩阵块。由同规格对角分块矩阵乘积法则

\[\begin{pmatrix} A_1& & \\ &...& \\ & &A_n\\ \end{pmatrix}· \begin{pmatrix} B_1& & \\ &...& \\ & &B_n\\ \end{pmatrix}= \begin{pmatrix} A_1B_1& & \\ &...& \\ & &A_nB_n\ \end{pmatrix}\]

所以在给大矩阵做对角化的时候，完全可以分别给每个小矩阵块做对角化再拼成分块对角大矩阵；观察联通块对角化后中心所夹的对角阵（特征值所组成的），每个连通分支（由上条定理）有且仅有一个0特征，则所拼成的大矩阵恰有连通分支个0特征。

DLC特性大放送：

L的次小特征值$\leq$点连通性（κ）$\leq$边连通性（λ）$\leq$最小度

最后一个等号：去掉最小度所对应的边必可使持有最小度的顶点孤立

仅给出点连通性（κ）<=边连通性（λ）的证明

取λ个边，记作边集E，删去E后图不连通，设其分为两个部分AB。

1°，存在点P，P不是E中任意边的端点。不妨设P在A部分，则删去E在A中的端点可使P孤立，删去的端点数必然小于λ

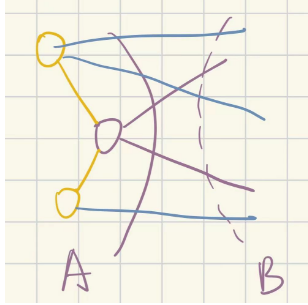
2°，所有原图中的顶点均是E中某（几）条边的端点，下证任意顶点的度均小于λ

不妨任取一个A部分中的顶点，在下图中记作紫圈，考虑由其自身引出的“桥梁”边集A（紫边）与非桥梁边B（黄边），则非桥梁边的另一个端点必在A侧（否则也是桥梁边），在下图中记作黄圈；由前提条件“顶点均是E中某（几）条边的端点”，可得每个黄圈必引出至少一条桥梁边（蓝边）；这使得一条黄边对应了多条蓝边，所以紫圈的度必定$\leqλ$

这种情况下边连通性（λ）=最小度

将紫圈直连的度个顶点去掉，必可使紫圈孤立，也即$κ\leqλ$

最小割最大流

最大流：在不超过边容量上限的情况下，尽可能的从源向汇输运更多流量

最小割：切断一些边，使源无法走到汇，且使Σ{切断的{容量上限}}尽可能小

最大流最小割的对偶性：

为了从LP方程式中看出这两个问题的对偶性，写决策变量和约束时要稍微注意一下，随心所欲的话是看不出对偶的

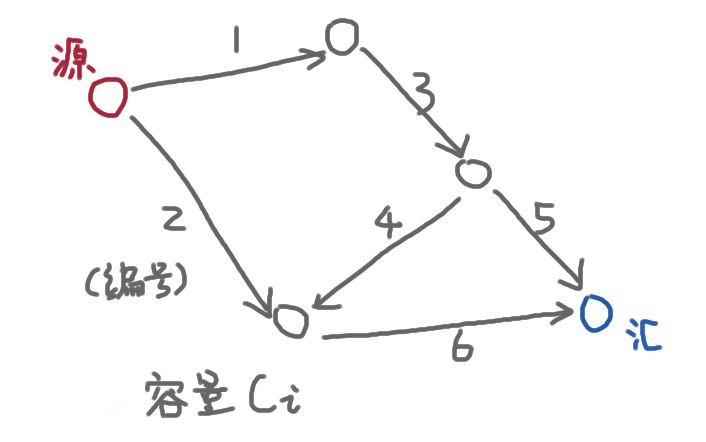
随便画的，后来发现13可以简并

（图中数字仅代表编号，i边上的容量是ci）这张图中从源到汇可行的路线是：135、1346、26，分别记为p1 p2 p3

首先考虑最大流问题，也就是把单路流量pi求和使其最大；限制条件：Σ经过该边的path流量$\leq c_i$

\[Max~~\sum_{i=1}^3 p_i\] \[\begin{pmatrix} 1&1&0\\ 0&0&1\\ 1&1&0\\ 0&1&0\\ 1&0&0\\ 0&1&1\\ \end{pmatrix} \begin{pmatrix} p_1\\ p_2\\ p_3\\ \end{pmatrix}\leq \begin{pmatrix} c_1\\ c_2\\ c_3\\ c_4\\ c_5\\ c_6\\ \end{pmatrix}\]

观察左边的矩阵，行代表边，列代表路径；如果第j条路径经过第i条边，那么就在i行j列填上1，否则留0.

下面考虑最小割问题，想作对每条路径上，必有边被割断（否则源和汇相连），决策变量是边$l_i$

\[Min~~\sum_{i=1}^6c_il_i\] \[\begin{pmatrix} 1&0&1&0&1&0\\ 1&0&1&1&0&1\\ 0&1&0&0&0&1\\ \end{pmatrix} \begin{pmatrix} l_1\\ l_2\\ l_3\\ l_4\\ l_5\\ l_6\\ \end{pmatrix}\geq \begin{pmatrix} 1\\ 1\\ 1\\ \end{pmatrix}\]

这两个LP表述中决策变量的范围我都省了

可以看出这是一个漂亮的对偶！由最大流的解存在性+强对偶定理可知最小割解存在且恰=最大流

接下来阐述算法思路

最大流算法：构造残差图，将原图和残差图叠在一起，再搜索源到汇的路径（也即给了每条路径撤销的机会），直到考虑撤销后也无法找到通路，则输出结果

最小割算法：（思考：切割值恰等于流量，那就是说只能切饱和边）承接最大流算法，我们可以知道每条边是否饱和。那么从源开始仅沿着非饱和边往前走，能走到的点就和源归为一团，直到某个时候仅走非饱和边再也走不动了（当然，此时肯定没有走到汇）；将路过的点和源抱团，剩下的归为另外一团，这两团间有且仅有饱和边相连，且恰好把源和汇分开，这些边就是我们要找的最小割。

import copy

G0 = [[0,10,5,15,0,0,0,0],
      [0,0,4,0,9,15,0,0],
      [0,0,0,4,0,8,0,0],
      [0,0,0,0,0,0,30,0],
      [0,0,0,0,0,15,0,10],
      [0,0,0,0,0,0,15,10],
      [0,0,6,0,0,0,0,10],
      [0,0,0,0,0,0,0,0]]

M = 10000

pathtable = []

def findpath(G,list=[0],flow=M):#把路径及流量打到表上
    global pathtable
    if list[-1]==len(G)-1:
        pathtable += [[list,flow]]
    else:
        st = list[-1]
        for i in range(0,len(G)):
            if G[st][i]>0 and st!=i and i not in list:
                findpath(G,list+[i],min(flow,G[st][i]))

def Flow(G,path,flow,sumflow):
    global pathtable
    G=copy.deepcopy(G)
    for i in range(0,len(path)-1):
        G[path[i]][path[i+1]]-=flow
        G[path[i+1]][path[i]]+=flow
    pathtable = []
    findpath(G)#把表打好
    if pathtable == []:
        return [G,sumflow+flow]
    else:
        return Flow(G,pathtable[0][0],pathtable[0][1],sumflow+flow)

def Getans(G1,G2):#G1是题目图，G2是已优化好的带残差的图，从中输出实际流量图G3，和仅存不饱和边图G4
    G3 = [[0 for i in range(0,len(G1))] for j in range(0,len(G1))]
    G4 = [[0 for i in range(0, len(G1))] for j in range(0, len(G1))]
    for i in range(0,len(G1)):
        for j in range(0,len(G1)):
            if G1[i][j] > 0:
                G3[i][j]=G1[i][j]-G2[i][j]
                if G2[i][j]>0:
                    G4[i][j] = 1
    return [G3,G4]

def ConnectionPoint(G,n=0):#检查图中n可以连接多少点，方法：从已连接的点集出发搜索，共搜索顶点-1轮
    Points = [n]
    for i in range(0,len(G)-1):#i代表搜索轮数
        for j in Points:#j代表出发点
            for k in range(0,len(G)):#k代表待定终点
                if G[j][k]!=0 and k not in Points:
                    Points += [k]
    return Points

def Bridge(G,points):#寻找点集points出去的桥们（最小割）
    edges = []
    for i in points:
        for j in range(0,len(G)):
            if G[i][j]>0 and j not in points:
                edges+=[[i,j]]
    return edges

findpath(G0)
MF=Flow(G0,pathtable[0][0],pathtable[0][1],0)
Gpair = Getans(G0,MF[0])
print('最大流量是')
print(MF[1])
print('达到最大流时的流量图为')
print(Gpair[0])

leftPoints = ConnectionPoint(Gpair[1])
ed = Bridge(G0,leftPoints)
print('最小割的边集是')
print(ed)
print('最小割的容量是')
c = 0
for e in ed:
    c+=G0[e[0]][e[1]]
print(c)

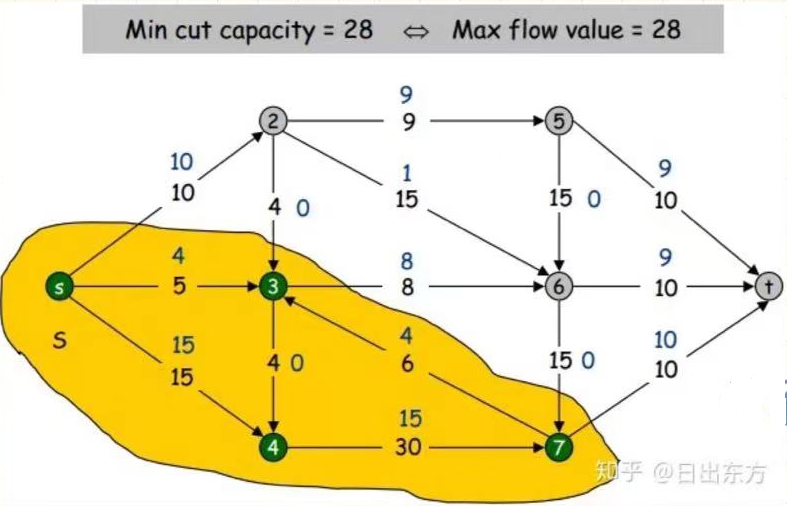
输出示例

最大流量是
28
达到最大流时的流量图为
[[0, 10, 5, 13, 0, 0, 0, 0], [0, 0, 0, 0, 9, 1, 0, 0], [0, 0, 0, 0, 0, 8, 0, 0], [0, 0, 0, 0, 0, 0, 13, 0], [0, 0, 0, 0, 0, 0, 0, 9], [0, 0, 0, 0, 0, 0, 0, 9], [0, 0, 3, 0, 0, 0, 0, 10], [0, 0, 0, 0, 0, 0, 0, 0]]
最小割的边集是
[[0, 1], [6, 7], [2, 5]]
最小割的容量是
28

最大割

因为这节课我的身体状态十分的差劲，所以相当于skip了，也许考前再补。。吧

这节课主要讲了：最大割问题是NP完全问题、一些布尔函数与NP问题之间的关系、最大割的近似算法（半正定规划松弛）

更新：我来补证明啦

P：所有可以在多项式时间内判定的问题的集合

NP：所有可以在多项式时间内验证的问题的集合

CNF：{只包含非运算和并运算}的布尔函数用且相连形成的大布尔函数；3-CNF限制了每个短函数长度为3（含三个变量）

SAT：判断某个CNF=1是否有解（此时每个括号内的取值不全为0）；3-SAT就是相应判断3-CNF是否有解

SAT就是每个括号里面要至少出一个1，有点像那种学代会每个班至少要去一个那种感觉

NAE-SAT：解在每个括号内的取值不全为0；且解在每个括号内的取值不全为1

就是除了要求每个班都得去一个人以外，还要求别班上所有人都去了，可能是想留人守教室吧

NAE-SAT的好处就是人员可以对调，让呆在教室里的人去开会，开会的人回来休息，还是满足要求的；也即变量全部取非也是解

性质：SAT和3-SAT和4-NAE-SAT和3-NAE-SAT都是NP完全的，所以下面我们利用这个性质去证明其他问题的NP完全

最大割问题的NP完全性证明：给定图𝐺和整数𝑘，判定𝐺中是否存在≥𝑘的割，这个问题是NP完全的，只需证明3-NAE-SAT可以规约至最大割问题

最大割NP完全的等价命题：对于一个n个变量m个括号的3-NAE-SAT有解<=>（这个3-NAE-SAT对应的）特定的带权图有至少为10nm+2m的割

如果3-CNF函数中有某个括号内同时含有xi与¬xi，那么这个括号值恒为1，把这个括号从函数中去掉对解没有影响，所以我们总可以假定3-CNF函数中不会出现某一个变量与自己的非出现在同一个括号中

从n个变量m个括号的3-CNF函数构造相应的带权图：

顶点代表着所有{xi}与{¬xi}，共2n个；边分为2类：

(1)同下标的xi与¬xi连边，权为10m；

(2)同一个括号里的三个顶点连边，权为1，边的总权为10nm+3m

从3-NAE-SAT的解确定割方案：变量的取值只可能是0或1，这自然将顶点分为两个部分，连接01值的边即为割边，它包括

(1)同下标的xi与¬xi连边，总边权为10nm；

(2)同一个括号里的三个顶点必有1个取值为a，2个取值为b，$a\neq b$，也即每个括号产生2条割边，所有括号共产生2m权的割。总计给出了10nm+2m大小的割

从至少为10nm+2m的割方案给出3-NAE-SAT的解：主要思想还是给割出来的两个顶点集，一边赋值1一边赋值0，证明这样的赋值恰为3-NAE-SAT的解

(1)首先xi与¬xi的边必须在割内，否则割大小最大为10(n-1)m+3m，比10nm+2m要小。（这保证了布尔变量的取值不会出现矛盾）

(2)其次对于每个括号产生的三角形，2-赋值方案只能有两种，即(1)全部同值(2)一个与其他两个不同值。很明显后者会比前者多2条割边，故取最大割时每个括号形成的三角形顶点取值总是一个与其他两个不同值，这恰符合3-NAE-SAT的要求

命题得证，所以最大割问题是NP完全的

思考：能否证明无权重最大割也是NP完全的?

从一篇论文里找到了无权最大割到2-MAX-SAT的规约方法，而2-MAX-SAT又可以归约到3-SAT上，是NP完全的，来源请见参考2

证明：

现在有一个2-SAT的布尔函数，设其为$f(x_1,…,x_n)=(a_1\vee b_1)\wedge(a_2\vee b_2)\wedge …\wedge(a_p\vee b_p)$;并且已知一组最优化的解，可以使得至多k句为真

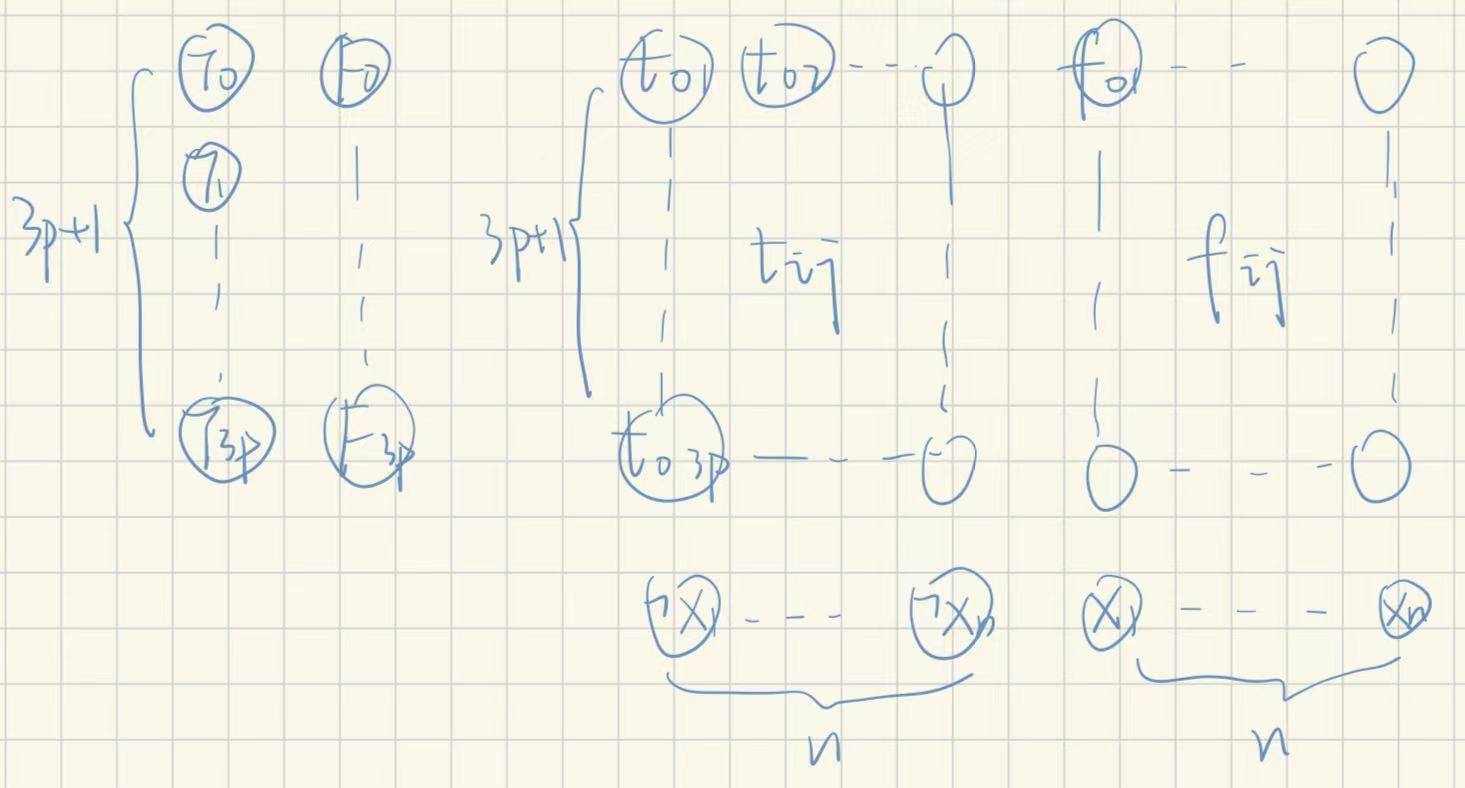
那么就可以根据这个来构建相应的图。图的顶点由三部分组成

第一部分（“矢量”部分，因为他们有一个下标）

(1)$T_0,…,T_{3p}$,共3p个

(2)$F_0,…,F_{3p}$,共3p个

第二部分（“矩阵”部分，因为他们有2个下标，另一个下标需要和自变量对应起来）

(1)$t_{ij};i\in{1,..,n},j\in{0,…,3p}$

(2)$f_{ij};i\in{1,..,n},j\in{0,…,3p}$

第三部分（自变量池）

(1)$x_1,…,x_n$（所有自变量）

(2)$\lnot x_1,…,\lnot x_n$（所有自变量的非）

那么顶点差不多就长这样

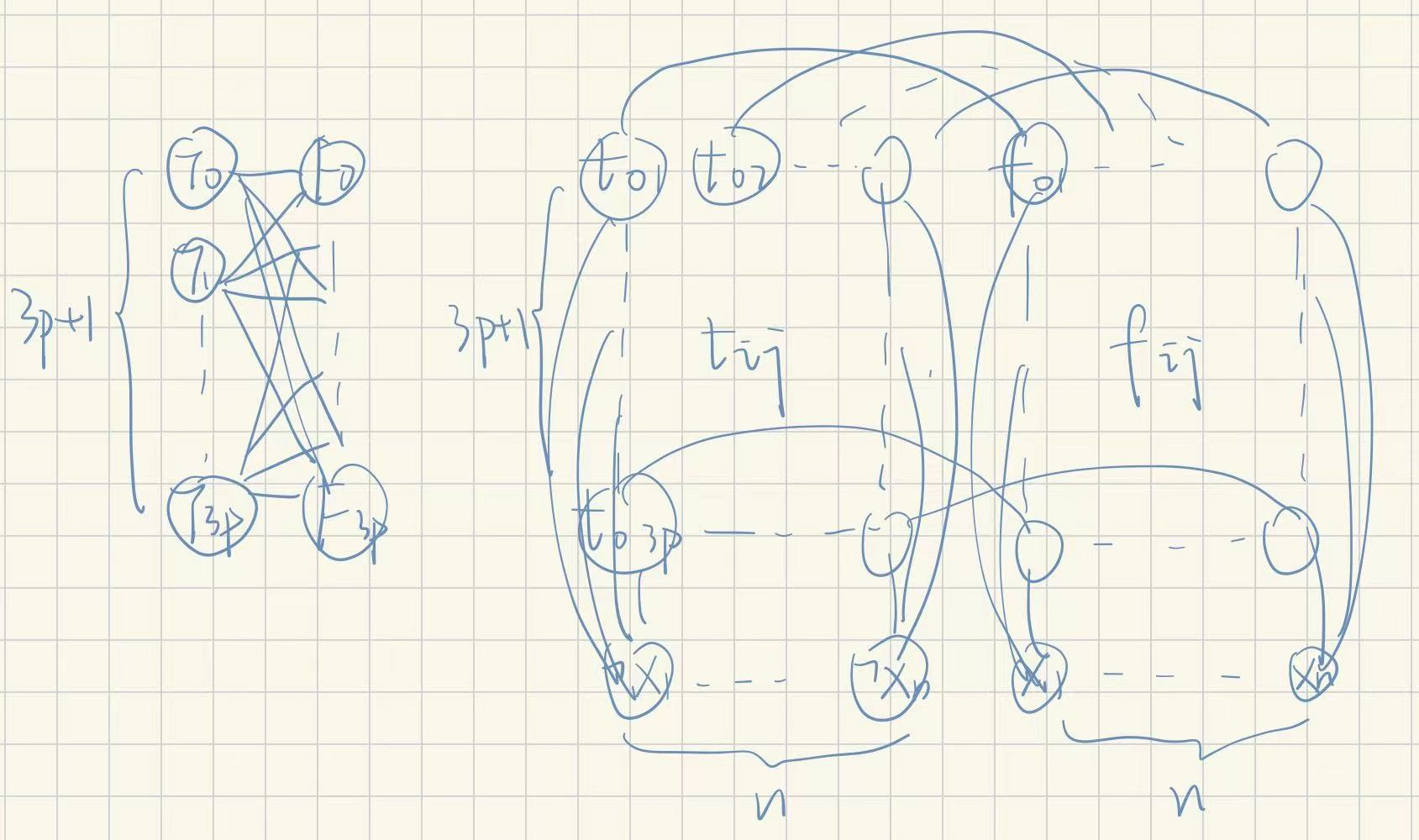
连边规则分两步进行，第一部分是连图的基本结构（也就是日后为最大割等价性垫背的），第二部分是根据具体的布尔函数连一些特殊的线（这些线才是真正将割与SAT问题联系起来的桥梁）

边第一部分

(1)任意的T与任意的F均相连，T与F之间构成最大边二部图（因为我希望最大割结果将T和P分成二部图）

(2)每个$f_{ij}$与对应的$t_{ij}$相连（因为我希望最大割结果中单列t和同列f不要在同一边）

(3)(这是最精彩的，就像老鹰捉小鸡一样)每一个$x_i$与对应的那一列$f_{ij},j=0,…,3p$均相连；对称的，一个$\lnot x_i$与对应的那一列$t_{ij},j=0,…,3p$均相连

第一部分连出来是这样的

对于仅有第一部分的边，可以找到不止一个割方案使得所有的边都是割边：只需满足(1)T与F不在同一侧；(2)任意x与自己的非不在同一侧；(3)任意x与它对应的那一列t同侧，任意非x与他对应的那一列f同侧（注意：在连边时，本来f是x的跟屁虫，t是非x的跟屁虫，然后你又让x与自己的非在异侧，这就导致所有跟屁虫与他们的保护伞都分开了，会使得割边很多）

记以上规则为“蓝边规则”，下面还要提到

并且这样的最优方案集的自由度恰为解的自由度！

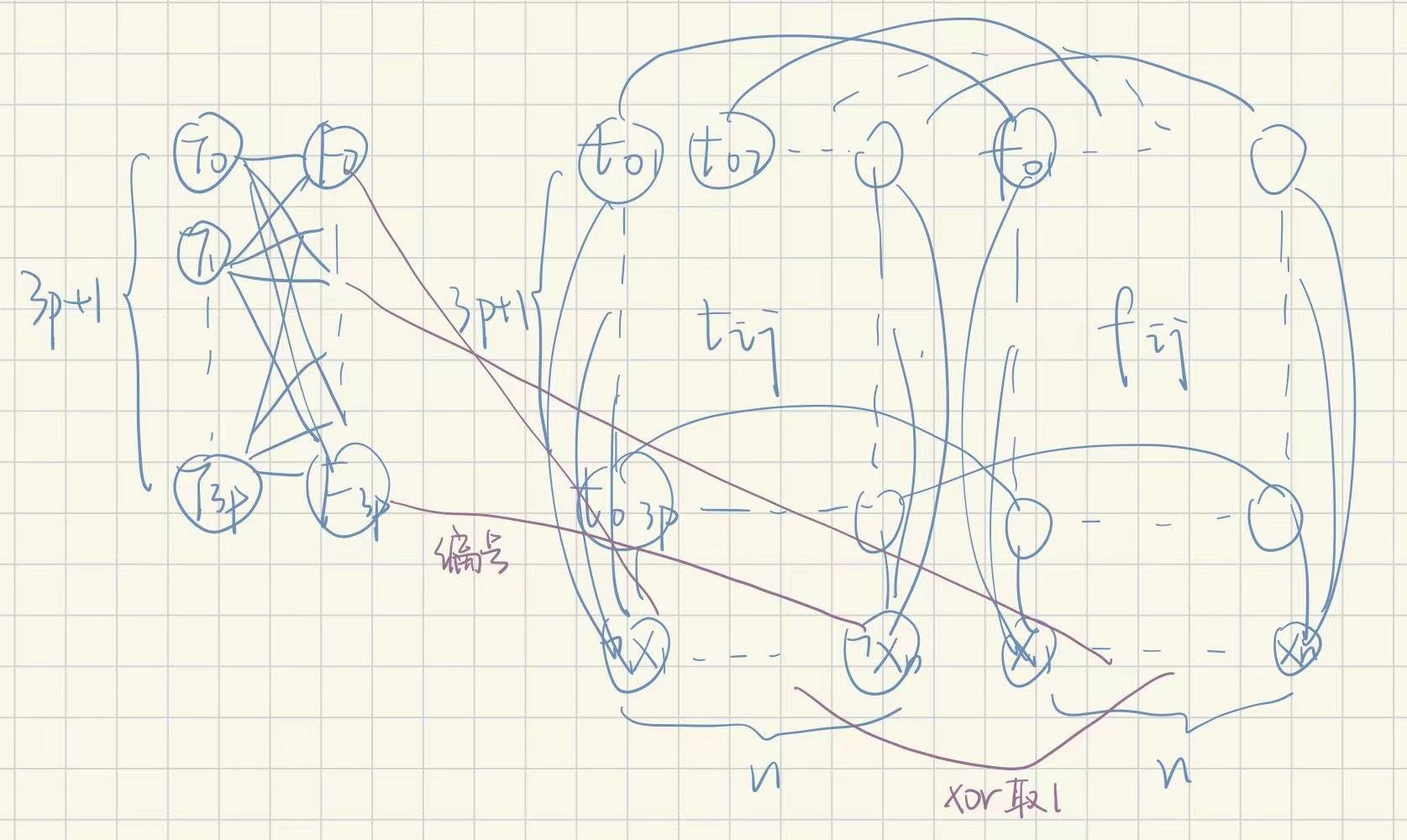
下面第二部分，再根据布尔函数的样子连更具体的边

(1)先给括号中的自变量按顺序用F来打上编号，即ai连$F_{2i-1}$,bi连$F_{2i}$，如图

(2)再根据解的特性，如果单句内的两个变量，它是通过异或来取到1的（也即(0,1);(1,0)），那么我们根据这样的解把这两个自变量之间连线

综上，第二部分中每个短句可以导出2~3个边，最后连出来这样（第二部分特定性太强，只能示意，用紫色笔标出）

最激动人心的时候到了，现在用2-MAX-SAT的解给出上图的一个割

割的一侧包括：所有的F+取0的自变量+这些自变量带领的一列t

蓝边（第一部分边）肯定是全部被割了这我们已经知道，现在来对每一个短句括号来看看紫边（第二部分边）的割情况

对于一个成立的短句，有两种情况(1)全1，那么这两个变量和F异侧，产生了两个割边；(2)0与1，那么1的变量与F贡献了一条割边，1与0因为异或成立又贡献了一条割边，总共还是2割边

对于一个不成立的语句，只能双取0，此时他们与F同侧，不会产生紫色割边

综上，当2-MAX-SAT问题至多成立k句时，紫色部分会带来2k个割边

再证明割集大小至少为蓝边 +2k的方案给出一个使得2-SAT成立k句的解：

由于紫边最多提供3p条割边，所以对于蓝边，任意一个对“蓝边规则”的改动均会至少损失3p+1条边，导致你紫边再怎么救也就不回来，所以最大割还是能保证“蓝边规则”的成立（这已经保证了布尔自变量取值的合法性，即x与非x异侧）

对于紫边，短句取1<=>提供两条割边；短句取0<=>提供0割边；并且有了上面的“蓝边规则”，可以保证一个括号只能提供2或0条割边，最大割的解严格给出了2-MAX-SAT的解

最后，我们将与F同侧的自变量赋值0，对面的变量赋值1，就得到了至少k个句为1的解。

近似算法：α真解≤算法输出的解≤真解

最大割的二次规划刻画

\[\max_{x_i\in\{-1,1\}}\sum_E\frac{1-x_ix_j}{2}\]

利用半正定规划松弛给出近似算法

对于上面的二次规划问题，x的取值放松至$R^n$上归一的向量，乘积改为向量内积

定义格拉姆矩阵$X_{ij}=\braket{x_i|x_j}$(一组向量造出来的Gram矩阵一定是半正定的，因为$\bra{c}X_{ij}\ket{c}=|\sum c_i\vec x_i|^2\ge0$)并且我证过实对称正定矩阵必可以分解为一组向量的$\braket{x_i|x_j}$形式

所以优化问题变为半正定规划

\[\max_{PSD~X,X_{ii}=1}\sum_{ij\in E}\frac{1-X_{ij}}{2}\]

进一步将这个规划推到纯矩阵上，定义矩阵内积$\braket{A|B}=\operatorname{tr}(AB)$,引入辅助矩阵C，Ak，必可以将这个规划写作

\[\min<C|X>\] \[subject~to~<A_k|X>=b_k,k=1,...,m~~;X~PSD\]

半正定规划优点：多项式时间内可计算

从半正定规划最优解还原出最大割问题的一个近似最优解：随机选择一个超平面，根据最优解所得到的一组单位向量在平面的左右侧来划分两个点集，中间所连边即为所求的割方案

下面计算这个还原算法给出的割大小均值

\[<\sum\frac{1-x_ix_j}{2}>=\sum P(x_i,x_j~apart)=\sum\frac{\theta_{ij}}{\pi}\]

而最优解$x_ix_j$可写作$cos\theta_{ij}$,下面求近似比

\[\alpha=\frac{\sum\frac{\theta_{ij}}{\pi}}{\sum\frac{1-cos\theta_{ij}}{2}}\ge\min\frac{\frac{\theta_{ij}}{\pi}}{\frac{1-cos\theta_{ij}}{2}}\sim0.878...\]

扩展图

扩展图指的是一类边较少，但连通性保持得很好的图

图上的Cheeger不等式要考，所以我得自己证一遍

对于d-正则图𝐺=([𝑛],𝐸)，有

\[\sqrt{2d\lambda(G)}\geq\phi(G)\geq\frac{1}{2}\lambda(G)\]

其中，λ(G)是G对应的拉普拉斯矩阵的次小特征值（也即邻接矩阵最大特征值与次大特征值之间的差，Spectral Gap）；$\phi(G)$指的是边扩展性：割边的数目除{较小割点集}的最小值

\[\phi(G)=min\frac{|C(S,T)|}{min\{S,T\}}\]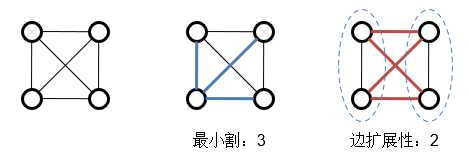

回忆一下前面提到的λ的谱表示（？名字瞎取的）

次小特征值λ的另一种表述：$λ=\min_{\sum x_i=0}\frac{x^TLx}{x^Tx}$（分量和为0是为了与(1,1,…,1)垂直）

证明$\lambda(G)\leq 2\phi(G)$:

构造性证明，关键在于构造向量

\[\vec y=(n-s)1_S-s1_T\]

其中1_S（1_T）是指示向量，每个位置对应一个点，如果这个端点在$S(T)$集中则填1，否则填0。我们来验证一下这个向量与1向量的正交性：

\[\vec y·\vec 1=(n-s)s-s(n-s)=0\]

非常好正交性，使我可以带入λ的定义式进行放缩

\[\lambda(G)\leq\frac{y^TLy}{y^Ty}\]

单独求一下y的2范数

\[y^Ty=((n-s)1_S^T-s1_T^T)((n-s)1_S-s1_T)=(n-s)^2s+s^2(n-s)=(n-s)sn\]

再求一下分子的二次型，注意到夹L的二次型等于带边差平方$\sum_{ij\in E}(x_i-x_j)^2$,所以分子为

\[\sum_{ij\in cut}(n-s+s)^2=n^2|C(S,T)|\]

所以

\[\lambda(G)\leq\frac{n^2|C|}{sn(n-s)}=\frac{n|C|}{s(n-s)}=\frac{n}{n-s}\phi(G)\leq2\phi(G)\]

下面来证$\sqrt{2d\lambda(G)}\ge\phi(G)$

考虑λ所对应的特征向量$\vec x$,重排顶点标号使得x中分量降序排列；如果x分量中正数较多，那就取个负号，使得分量中正数不多于非正数。

然后大概就是这样

对于任意的$l\in[1,n-1]$，用l将有序顶点列分割成两块，形成一个割方案，所以有

\[\phi(G)\le\min_{l\in[n-1]}\frac{|C_l|}{min\{l,n-l\}}\]

将特征向量x按分量符号截断，$y=[x_1,…,x_k,0,…,0]^T$，使得前k项>0的分量保留，而后面清零

引理1：$R(y)=\frac{y^TLy}{y^Ty}\le\lambda(G)=R(x)=\frac{x^TLx}{x^Tx}$

证明：关键在于放缩Ly的前k项分量、

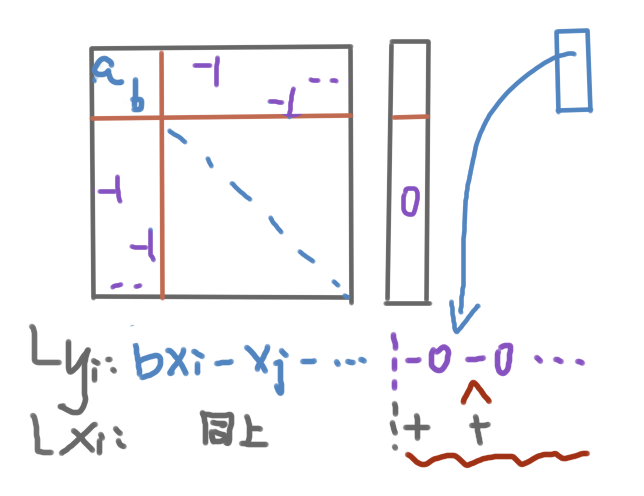
看示意图，本来在计算Lx的时候，尾巴可能有几个(-1)乘非正项，也就是非负项，但是在计算Lyi中这些非负项被0截断了，所以$\forall i\in[k],(Ly)_i\le (Lx)_i=\lambda x_i$（Ly的每个分量都不大于Lx）

现在再左乘一个yT计算内积,因为yT后面有0尾巴，所以对于Ly的后面几项也不起作用

\[y^TLy=\sum_{\le k}y^i(Ly)_i\]

因为yi是严格正的，所以可以通过Lyi的放缩对这个和式进行同向放缩

\[\forall i\in[k],(Ly)_i\le (Lx)_i=\lambda x_i\] \[y^TLy=\sum_{\le k}y^i(Ly)_i\le\sum_{\le k}y^i\lambda x_i=\sum_{\le k}x^i\lambda x_i=\lambda\sum_{\le k}x^i x_i\] \[\frac{y^TLy}{y^Ty}\le\frac{\lambda\sum_{\le k}x^i x_i}{\sum_{\le k}x^i x_i}=\lambda~~\boxed{}\]

引理2：对于$\forall y\in[0,1]^n$和d-正则图，存在顶点子集S满足

\[\frac{|C(S,[n]-S)|}{|S|}\le\sqrt{2dR(y)}\]

证明（新奇的概率证明）：

均匀随机选取参数$t\in[0,1]$,利用t作为及格线，yi^2作为分数，对点集进行划分

\[S(t)=\{i:y_i^2>t\}\]

这样就确定了一个割方案，现在算算割边的期望,就是对着图上的每一条边，揪着它问：你好，你能连接割的两边吗？你连接割的两边的概率是多少？然后把这个概率加起来

\[<|C(S,[n]-S)|>=\sum_EP(i\in S,j\notin S)=\sum_EP(y_j^2\leq t\leq y_i^2)=\sum y_i^2-y_j^2\] \[\sum y_i^2-y_j^2=\sum(y_i+y_j)(y_i-y_j)\le\sqrt{\sum(y_i-y_j)^2}\sqrt{\sum(y_i+y_j)^2}\]

其中

\[\sum_E(y_i-y_j)^2\le2\sum_E(y_i^2+y_j^2)=2d\sum_Vy_i^2\]

故

\[<|C(S,[n]-S)|>\leq\sqrt{2d\sum_E(y_i-y_j)^2}\sqrt{\sum_V y_i^2}\]

下面计算分母S的期望

\[<|S|>=\sum y_i^2\]

下面就是见证概率魔法的时候咯（虽然很想直接把这两个期望一除，但是这是没有道理的，还得用乘积式移项绕个弯）

\[<|C|>-\sqrt{2dR(y)}<|S|>\le0\] \[<|C|-\sqrt{2dR(y)}|S|>\le0\]

用到的原理：期望<=0,则必存在一个t取法，使得这个值就是<=0的

\[\exists t\in[0,1],s.t.\frac{|C(S,[n]-S)|}{|S|}\leq\sqrt{2dR(y)}~~\boxed{}\]

终于进入主证明环节了！在这里面贯通始末的是在引理1排好的特征向量x和截断后得到的向量y

由于$y\in [0,1]^n$,所以直接代引理2，存在割方案S使得$\frac{|C|}{|S|}\le\sqrt{2dR(y)}$;又因为y中大半都是0，所以拿非负t当作及格线划分，及格的点集数$|S|$一定是小半，即$|S|\le n/2$，这是满足φ定义式的

\[\phi(G)=min\frac{|C|}{min\{|S'|,n-|S'|\}}\le\frac{|C(S,[n]-S)|}{|S|}\le\sqrt{2dR(y)}\le\sqrt{2d\lambda(G)}~\boxed{}\]

计算超立方体的λ：见“布尔函数敏感度”节下的证明，λ=2，代入不等式得φ=1

匹配与覆盖

匹配：两个点配成一对；覆盖：每条边必然有一条手被挑中（，这样挑中的点集）

二部图的最大匹配=最小顶点覆盖

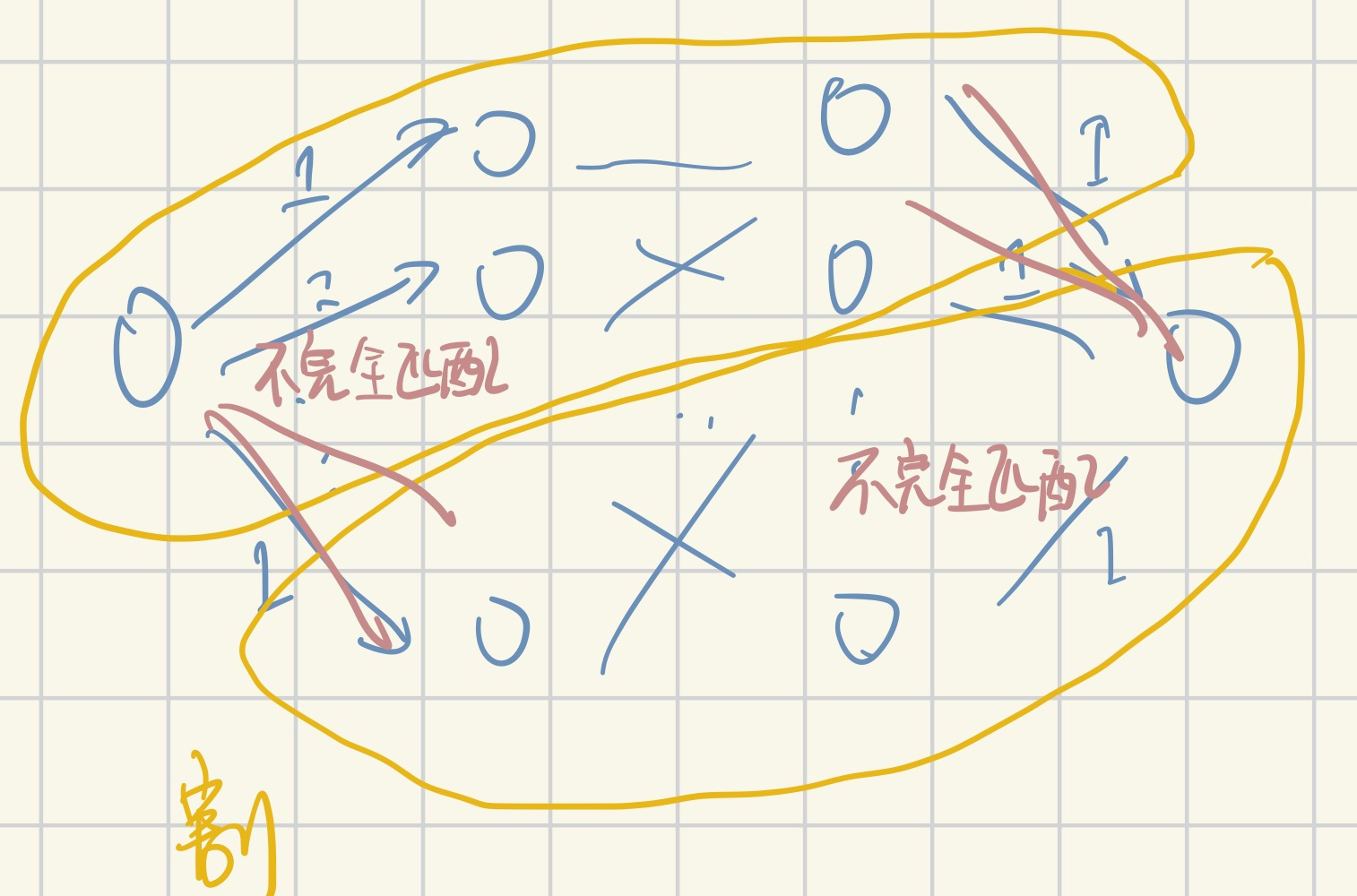
证明：规约到之前的最大流最小割问题来考虑，在二部图的左右加上源与汇，分别连上左右的点，为方便就称它外部边；令连上源汇的边容量为1，而二部图本身的边流量为∞，为方便就称它内部边

那么在这个图中，必然存在最大流=最小割；最大流=Σ利用的外部边，而每条利用的边恰对应一个有匹配的原点，所以最大流=最大匹配

现在考虑最小割，由于内部边流量为∞，所以最小割一定不会去割内部边；也即，最小割恰把二部图分为两个不连通的子图。如图，不妨先考虑上面一部分子图，右上角割边恰等于上部{左点}与{右点}中数目较少的点数，那么这一群较少的点必然能将上部所有内部边覆盖（若有边不与右上角点相连，那他一定跨过割线到下半部了）；下半部分同样给出了子图的最小顶点覆盖

由于二部图在黄割线处本身就有一个裂痕（没有边相通），所以原图的最小覆盖必定同时是这两部分子图的最小覆盖，所以最小割=最小覆盖 => 最大流=最小割=最大匹配=最小覆盖

二部图的婚配定理

二部图中存在完美匹配<=>对于任何一个大小为a的单侧边子集，与他相连的另一侧点数>=a

充分性由完美匹配方案易得

必要性

仅需证明最小点覆盖是全单侧点数N

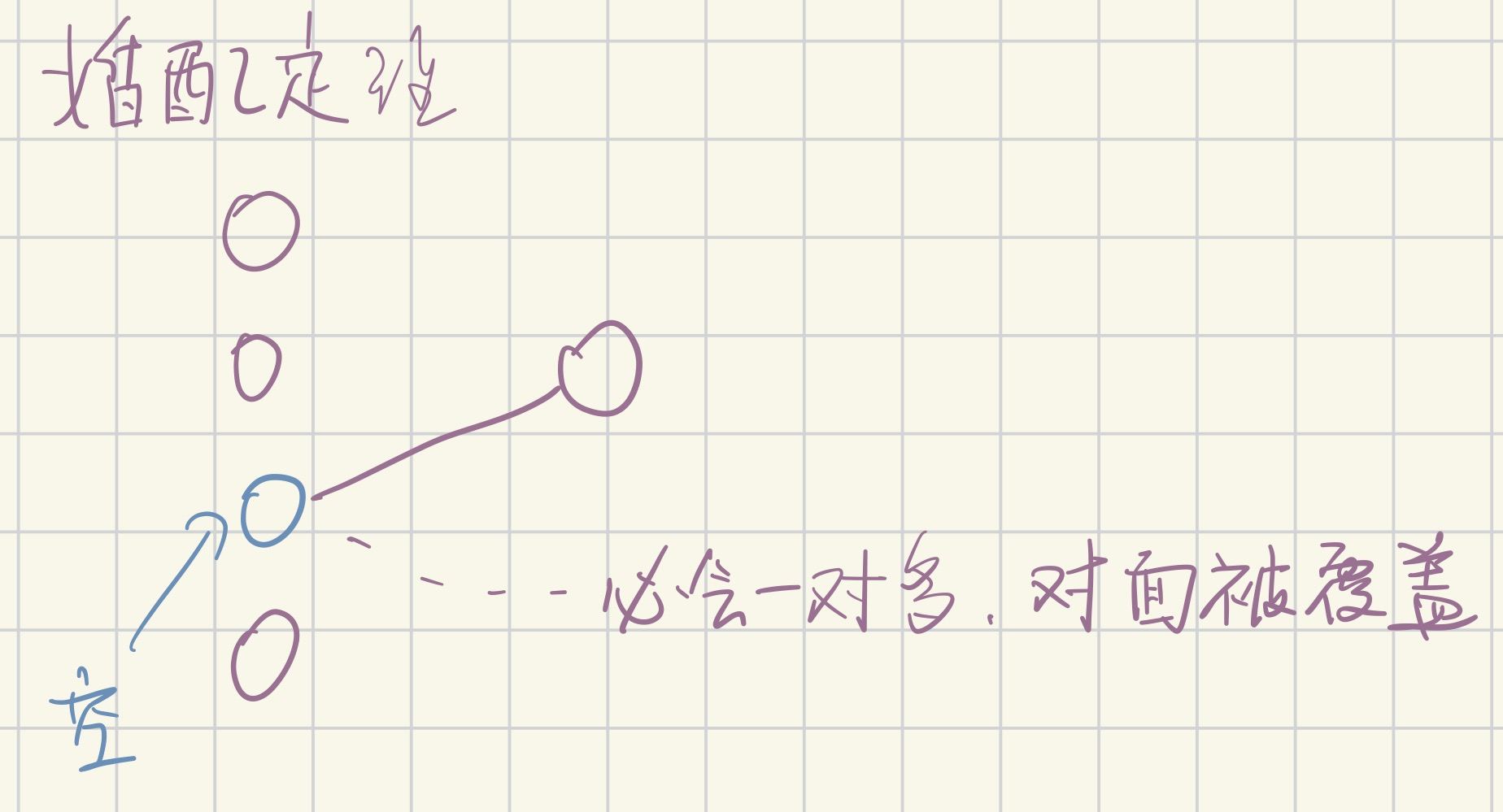
先取出原图的任意一个覆盖S，观察在左侧却不在S中的点，设为b个，他们必与右侧>=b个点相连，且右边这>=b个点必在边覆盖集中，故边覆盖数目>=N-b+b=N，最小覆盖必定是N，所以一定存在完美匹配

洗袜子-打火机引理（Schwarts-Zippel Lemma）

对度为d的非零n变量多项式$p(\vec x)$,均匀随机地从集合$S\subseteq R^n$中选择$\vec x_0$，则

\[P[p(\vec x)=0]\le \frac{d}{|S|}\]

使用数学归纳法，对变量数n进行归纳；当n=1时由代数基本定理可得命题成立，假设n<=k处成立，下证n=k+1处成立

在p(x)中取$x_{k+1}$的最高次项，设最高次为l，则对p(x_{k+1})进行带余除法

\[p(\vec x_{k+1})=x_{k+1}^lq(\vec x_k)+r(\vec x_{k+1})\]

其中，$q(\vec x_k)$度至多为d-l，$r(\vec x_{k+1})$度至多为l-1,都可以利用归纳假设

利用条件概率的拆分

\[\begin{aligned} P[p(\vec x_{l+1})=0]&=P[p(\vec x_{l+1})=0]·P[q(\vec x_k)=0]+P[p(\vec x_{l+1})=0]·P[q(\vec x_k)\neq0]\\ &\le P[q(\vec x_k)=0]+P[p(\vec x_{l+1})=0]·P[q(\vec x_k)\neq0]=\frac{d-l}{|S|}+\frac{l}{|S|}=\frac{d}{|S|} \end{aligned}\]

上式用到的道理：当$q(\vec x_k)\neq 0$时，$p(\vec x_{k+1})$化为关于$x_{k+1}$单变量的l次多项式，可以用代数基本定理

下面定义一个Edmonds矩阵：将邻接矩阵中每个为1的位置换成一个变量（例如，第i行第j列的1可以换成$x_{ij}$

二部图存在完美匹配<=>Edmonds矩阵行列式多项式不为0多项式

高速证明：因为行列式的每一项都对应一个置换，完美匹配在邻接矩阵中也正好对应一个置换

对于可以不是二部的无向图，再定义一个矩阵A’：同样是邻接矩阵1改变量，但是要保持矩阵的反对称性（对角线正反是同一个变量加负号）

无向图存在完美匹配<=>刚刚定义的A’矩阵行列式多项式不为0多项式

高速证明：行列式每一项对应一个置换，每个置换对应着多个环（这里的环包括两点一边结构）；而对于奇数长度置换句，必存在他的逆，而他的逆由于反对称性出现在det多项式中必然仅与原置换反号，加和时会消掉，也就是说det多项式中只会包括偶数长度置换轮以及他们的无交复合；而对于每个偶数点的环，必存在完美匹配，故原命题得证。

计算二部图是否存在最大匹配的随机算法：Lovász算法：给变量随机赋值，计算Edmonds矩阵的行列式对应的多项式值是否为0

若不存在完美匹配，则det多项式是0多项式，赋值后结果一定是0

但是存在完美匹配时，det多项式不是0多项式，大概率算得结果非0，除了如果取值很巧地落在了多项式的根上，那么就输出0了

成功率分析：度为n，变量数为n^2，代入洗袜子打火机引理得取值全集大小为n^3时，若存在完美匹配，则输出正确概率为1-1/n^2

习题1： Lovász算法的分析能否推广至$|𝐿|\neq|𝑅|$的情形？

答：可以。不妨设$|L|<|R|$,此时Edmonds矩阵变为扁矩阵，问题变为是否有大小为$|L|$的匹配方案。

而在矩阵上表现为：存在大小为$|L|$的匹配方案<=>Edmonds扁矩阵行满秩<=>Edmonds扁矩阵去掉数列后得到的方阵行列式不为0

所以只需要依次抽掉数个列向量，套用Lovász算法即可，共需迭代$C_{|R|}^{|R|-|L|}$次

习题2： Lovász算法能否用于计算最大匹配？

答：可以，有两种方法

(1)计算Edmonds矩阵的秩，即为最大匹配，时间复杂度为O(n^3)

(2)硬要用Lovász算法的话，那就依次去掉一行一列，利用Lovász算法计算余子式，但是这样做时间复杂度太高了

独立数与香农容量

柯西交错定理：在矩阵线性空间End(W)内，A是n阶实对称矩阵，B是A的m阶主子阵(从A的第k个对角元取至第k+m-1个对角元)，将A和B的特征值分别从大到小排列($\lambda_1(A)\geq\lambda_2(A)\ge…\ge\lambda_n(A)$,B同理)，则有

\[\lambda_{n-m+i}(A)\le\lambda_i(B)\le\lambda_i(A)\]

证：按照特征值的排列顺序将对应的特征向量取出来，记作$x_i(A),i=1,2,..,n$

令$V(A)=span(x_i(A),i=k,k+1,…,n)$,则$V(A)\subset W ;dimV(A)=n-k+1$

令$x’_i(B)=(0,..,0,x_i(B)^T,0,..,0)^T$，前面补k-1个0，后面补n-(k+m-1)个0（使得特征向量所在位置与主子式B在A中位置一致，并补齐至n维长度）

令$V’(B)=span(x_i’(B),i=1,2,…,k)$,则$V’(B)\subset W ;dimV’(B)=k$,$V(B)=span(x_i(B),i=1,2,…,k)$

由于$dimV(A)+dimV’(B)=n+1>dim(W)$,故$\exists v\neq 0,v\in V(A)\cap V’(B)$

可以记$v=(0,..,0,y(B),0,…,0),y\in V(B)$

则二次型

\[v^TAv=y^TBy\]

又因为特征值可以化为如下优化问题

\[\lambda_k(A)=\max_{z\in V(A)}\frac{z^TAz}{z^Tz};\lambda_k(B)=\min_{z\in V(B)}\frac{z^TAz}{z^Tz}\]

故

\[\lambda_k(A)=\max_{z\in V(A)}\frac{z^TAz}{z^Tz}\ge\frac{v^TAv}{v^Tv}=\frac{y^TBy}{y^Ty}\ge\min_{z\in V(B)}\frac{z^TAz}{z^Tz}=\lambda_k(B)\]

即

\[\lambda_i(B)\le\lambda_i(A)\]

再取$W(A)=span(x_i(A),i=1,…,m-k+1)$,$W(B)=span(x_i(B),i=k,k+1,..,m)$

此时

\[\lambda_{m-k+1}(A)=\min_{z\in W(A)}\frac{z^TAz}{z^Tz};\lambda_k(B)=\max_{z\in W(B)}\frac{z^TAz}{z^Tz}\]

同理可得

\[\lambda_{n-m+i}(A)\le\lambda_i(B)\]

实对称矩阵A的惯性$n_{\geq 0}(A)$：A的非负特征值数目

图的独立数$\alpha(G)$：图中最大独立集（两两之间没有边）点数目

则独立数有惯性上界（A(G)是带权邻接矩阵）

\[\alpha(G)\le n_{\geq 0}(A(G))\]

证明：独立集在邻接阵中表现为全0的主子式，故A(G)中任意独立集构成的主子式B的0特征数不超过$\alpha(G)$

记B是k阶全0方阵($k\le\alpha(G)$)，则

\[0=\lambda_k(B)\le\lambda_k(A)\]

故A的非负特征数必>=k,k至大为独立数α，也即$n_{\geq 0}(A(G))\ge \alpha(G)$

图的强积：将点做张量积，若原图均有边（点与自己之间视作有边）则强积后的图有边

有噪信道的精准通信容量：$C(N)=\sup_{k\in N}\sqrt[k]{c(N^{\otimes k})}=\lim_{k\to\infty}\sqrt[k]{c(N^{\otimes k})}$

图的香农容量：$\Theta(G)=\sup_{k\in N}\sqrt[k]{\alpha(N^{\boxtimes k})}=\lim_{k\to\infty}\sqrt[k]{\alpha(N^{\boxtimes k})}$

性质:$c(N\otimes N’)=\alpha(G_N\boxtimes G_{N’})\ge\alpha(G_N)\alpha(G_{N’})=c(N)c(N’)$

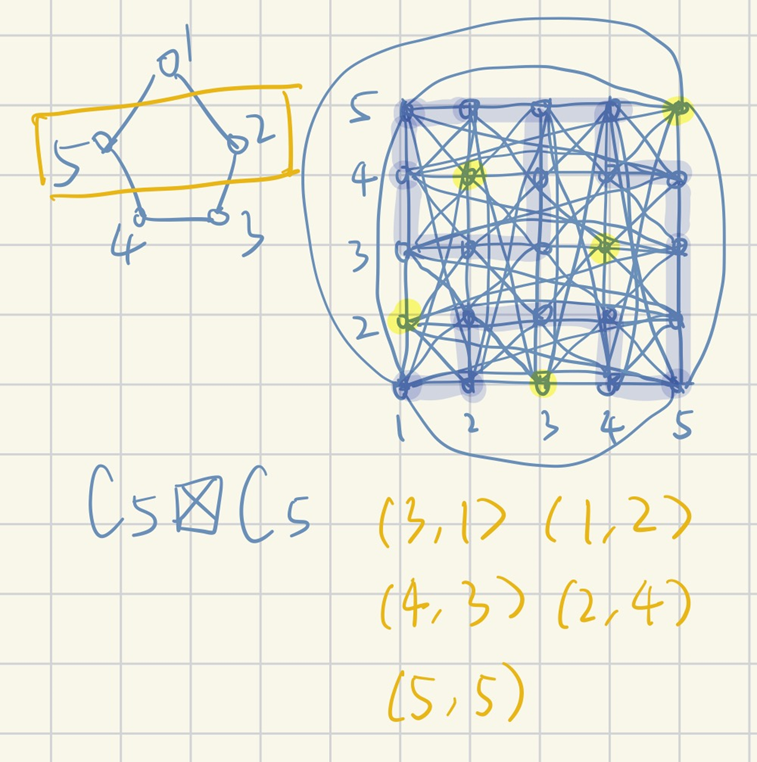
强积之后，独立数有扩张

超可乘性证明：仅需证明强积图$G_1\boxtimes G_2$必然包含大小为$\alpha(G_1)·\alpha(G_2)$的独立集

设$G_1$中的最大独立集为$A_1$，且设$B_1=G_1-A_1$,对下标为2的情况同理

下证大小为$\alpha(G_1)·\alpha(G_2)$的点集$C={(x,y)\in G_1\boxtimes G_2|x\in A_1,y\in B_1}$构成独立集

任取$P_1(x_1,y_1),P_2(x_2,y_2)\in C,P_1\neq P_2$,不妨设$x_1\neq x_2$

由于$x_1,x_2\in A_1$，故$x_1$与$x_2$之间没有边，故$P_1$与$P_2$之间没有边，而P的选取是任意的，故C是图$G_1\boxtimes G_2$内的独立集，也即

\[\alpha(G_1\boxtimes G_2)\ge\alpha(G_1)\alpha(G_2)\]

证明α的sup=lim：(Fekete lemma,抄自参考1)

记$f(n)=\alpha(N^{\boxtimes n}),n\in Z_{\ge}$,则正函数f满足$f(a+b)\ge f(a)f(b)$

对n进行带余除法(m>0)

\[n=km+r;k=\lfloor \frac{n}{m}\rfloor, 0\le r<m\]

则有不等式

\[f(n)\ge f(m)^k+f(r)\]

同开n次根号，得

\[f(n)^\frac{1}{n}\ge f(m)^\frac{k}{n}+f(r)^\frac{1}{n}\]

令$n\to\infty$,由于$f(r)$有界，故$f(r)^\frac{1}{n}\to 0$,且

\[\lim_{n\to\infty}\frac k n=\lim_{n\to\infty}\frac{1}{n}\lfloor\frac{n}{m}\rfloor=\frac{1}{m}\]

代回得

\[\lim_{n\to\infty}f(n)^\frac{1}{n}\ge f(m)^\frac{1}{m}\]

对等式左侧，有

\[\sup_n f(n)^\frac{1}{n}\ge \lim_{n\to\infty}f(n)^\frac{1}{n}\ge f(m)^\frac{1}{m}\]

由于m可取任意正整数，上式均成立，故取某一个值使得f(m)/m极大

\[\sup_nf(n)^\frac{1}{n}\ge \lim_{n\to\infty}f(n)^\frac{1}{n}\ge\sup_nf(n)^\frac{1}{n}\]

也即

\[\lim_{n\to\infty}\sqrt[n]{\alpha(N^{\boxtimes n})}=\sup_n\sqrt[n]{\alpha(N^{\boxtimes n})}\]

图的正交表示：d维实空间中的一组与顶点一一对应的向量，向量之间正交当且仅当点与点之间没有边连接

洛瓦兹θ函数：对于图的所有正交表示内所有长度为1的向量c，c与正交表示向量内积平方的最小值的倒数（这是真说不明白，还是看式子吧）

\[\theta(G)=\min_{OR(G),||c||=1}\max_{i\in[n]}\frac{1}{<c|v_i>^2}\]

分数阶团覆盖是香农容量的上界，而比分数阶团覆盖小的洛瓦兹θ函数是更好的上界

分数阶团覆盖α*(G)定义为

\[\alpha^*(G)=\max\{\sum_{i\in[n]}t_i:t_i\ge0,\sum_{i\in C}t_i\le1\forall clique~C~of~G\}\]

习题：证明$\alpha^*(C_5)=5/2$

答：设五边形顶点上的参数依次是a,b,c,d,e,则由分数阶团覆盖的限制条件有

\[a+b\le1~;b+c\le1~;c+d\le1~;d+e\le1~;e+a\le1\]

要求$\max a+b+c+d+e$，那就直接把上面五个不等式加起来除个2，就能得出

\[\alpha^*(C_5)=\max a+b+c+d+e=5/2\]

习题2：证明对任意的图𝐺,𝐻， 𝛼∗(𝐺⊠𝐻)≥𝛼∗(𝐺)𝛼∗(𝐻)也成立

答：设G(n,E)的每个顶点取到分数阶团覆盖的值设为$g_i$，H(m,W)的每个顶点取到分数阶团覆盖的值设为$h_i$，他们满足一个团内求和不大于1

对于图𝐺⊠𝐻中的顶点$(i,j)$，先赋予参数$g_ih_j$，如果这是一个合法的分数阶团覆盖参数取值，那么$\alpha^*(G\boxtimes H)\ge\sum_{i\in[n]}\sum_{j\in[m]}g_ih_j=(\sum_{i\in[n]}g_i)(\sum_{j\in[m]}h_j)=\alpha^*(G)\alpha^*(H)$

下面来说明这个参数取值是符合分数阶团覆盖要求的

对于𝐺⊠𝐻中的任意一个团，设他们的第一个坐标（来自G中顶点的）构成G中的顶点子集G’,设他们的第二个坐标（来自H中顶点的）构成H中的顶点子集H’，由于强积图中任意量纲顶点之间有边，故G’是G中的团，H’是H中的团，即

\[\sum_{i\in G'}g_i\le1~;~\sum_{i\in H'}h_i\le1\]

那么在𝐺⊠𝐻的团中

\[\sum_{(ij)~in~clique}g_ih_j\le(\sum_{i\in G'}g_i)(\sum_{i\in H'}h_i)\le1\]

也即强积图的团顶点参数和不超过1，该参数取值合乎要求，证毕

验证：$<v_i\otimes u_j|v_k\otimes u_l>=<v_i|v_k><u_j|u_l>$

\[v_i\otimes u_j=(v_{i1}\vec u_j,v_{i2}\vec u_j,...,v_{in}\vec u_j)\] \[v_k\otimes u_l=(v_{k1}\vec u_l,v_{k2}\vec u_l,...,v_{kn}\vec u_l)\] \[\begin{aligned} <v_i\otimes u_j|v_k\otimes u_l>&=v_{i1}v_{k1}<u_j|u_l>+v_{i2}v_{k2}<u_j|u_l>+...v_{in}v_{kn}<u_j|u_l>\\ &=<v_i|v_k><u_j|u_l> \end{aligned}\]

Haemers上界：和洛瓦兹θ函数相比没有优劣的断言（不同图不一样）

图的矩阵表示：行数=列数=顶点数的对称矩阵，对角线全部为1，矩阵分量为0当且仅当两个点之间没有边

Haemers上界：和洛瓦兹θ函数相比没有优劣的断言（不同图不一样）

图的矩阵表示：行数=列数=顶点数的对称矩阵，对角线全部为1，矩阵分量为0当且仅当两个点之间没有边

Haemers上界H(G)是矩阵表示的最小秩

习题：证明半正定矩阵的Haemers上界不小于洛瓦兹θ函数

引理：所有半正定实对称nxn矩阵都有Gram分解，也即分解为一个矩阵与他的转置的乘积$VV^T$，分解出的矩阵规格为nxr，r是原半正定矩阵的秩

证明：所有实对称矩阵A必可以对角化，且可以有一组完备的互相正交归一的本征矢，记作
\[A=P\Lambda P^{-1}\]
其中，$\Lambda$是对角阵；由于P是正交矢量组成的矩阵，所以$P^{-1}=P^T$，故
\[A=P\Lambda P^T\]
当A是半正定矩阵时，$\Lambda$中的分量只有非负数；将$\Lambda$中的特征值和P中的特征向量调整顺序，总可以使得$\Lambda$中的前r(A)个分量是正数，后n-r(A)个分量为0；构造矩阵，使得
\[L_{ii}=\sqrt{\Lambda_{ii}}\]
因此L的后n-r(A)个分量同样为0，此时
\[A=P\Lambda P^T=PLL^T P^T=(PL)(PL)^T\]
其中，由于L的后n-r(A)个分量为0，所以PL的后n-r(A)列为0；$(PL)(PL)^T$的效果等同于PL去掉全为0的后n-r(A)列，也即nxr(A)规模的矩阵与自己的转置相乘。所以把PL的后n-r(A)列砍掉之后就是符合条件的V，找到了Gram分解

进一步地，将V的每一行看作一个行向量xi，我们就可以将这个半正定实对称矩阵写作$\braket{x_i|x_j}$的形式，对角元是每个向量模方

设这个半正定矩阵的秩是d。有了这个引理之后，我们可以将半正定矩阵表示中的ij分量视作第i个V中的行向量与第j个V中的行向量作内积；由于矩阵分量为0当且仅当两个点之间没有边<=>对应的两个向量垂直；而对角线元素即为向量长度，他们都是1说明这一组行向量是归一化的，这恰好满足$R^d$线性空间中正交表示的要求，设这组表示向量（原V中行向量）为{vi}

原命题转化为证明洛瓦兹θ函数<=d

上面的正交表示还需要做进一步处理，考虑自张量空间中的表示$v_1\otimes v_1,v_2\otimes v_2,…,v_n\otimes v_n\in R^n\otimes R^n$,它同样也是正交表示（验证模长、内积为0与无边的充要性），并设该空间的正交归一基矢为$e_i\otimes e_j,i,j\in[1,n]$

现在希望找到一个与所有表示矢量$v_i\otimes v_i$内积都恒定为$1/\sqrt{d}$的$c$

构造$c=\frac{1}{\sqrt{d}}\sum_{i=1}^de_i\otimes e_i$,则验证模长

\[<c|c>=\frac{1}{d}\sum_{i=1}^d 1=1\]

满足洛瓦兹θ函数的限制条件,现在来算c与任意表示矢量的内积

\[\forall i,<c|v_i\otimes v_i>=\frac{1}{\sqrt{d}}\sum_{j=1}^d<e_j\otimes e_j|v_i\otimes v_i>=\frac{1}{\sqrt{d}}\sum_{j=1}^d<e_j|v_i>^2=\frac{1}{\sqrt{d}}||v_i||=\frac{1}{\sqrt{d}}\]

回到洛瓦兹θ函数的表达式

\[\theta(G)=\min_{OR(G),||c||=1}\max_{i\in[n]}\frac{1}{<c|v_i>^2}\]

在以确定的表示，以确定的c，而在max的优化过程中，值恒为$d$，所以总的来看加上min的优化条件以后有

\[\theta(G)\le d\]

证毕

染色数

平面图：V-E+F=2（边可以无交叉）

证明：平面图总有5-染色方案数

记区域f的读deg(f)为绕f封闭游走的最短经过线段数，则有$\sum_f \operatorname{deg}(f)=2|E|$

当所有区域度>=3时，有$3|F|\le 2|E|\Rightarrow 3|V|-|E|\ge 6$

又因为$3|V|-|E|=\frac{1}{2}\sum_v(6-\operatorname{deg}(v))$，所以必然存在度小于等于5的顶点

利用数归证明，首先对小于等于5个顶点的图均成立；然后假设对顶点小于n的成立，考虑一个顶点有n个的平面图，取出那个度小于等于5的顶点P，剩下的子图满足5-染色，也就是说现在主要考虑怎么在5-染色情况下加入P

如果P的度很低就不用说，直接上多余的颜色，仅需考虑度为5的情况

如下图，如果两个邻居没有另外一条路相连，则可以通过连接图全反色(红<->黄)来使两个邻接同色，可以将顶点上剩下的一色

如果两个邻居相连，则在考虑另两个邻居，他们必定不是相连的（否则不是平面图），再对这两个邻居进行换色操作合并颜色即可，证毕on

染色数的优化表达：

\[\chi(G)=\min\sum_{I\in I(G)}\lambda_I;\lambda_I\in\{0,1\},\sum_{I\in I(G)}\lambda_I\chi^I=1_{|V|}\]

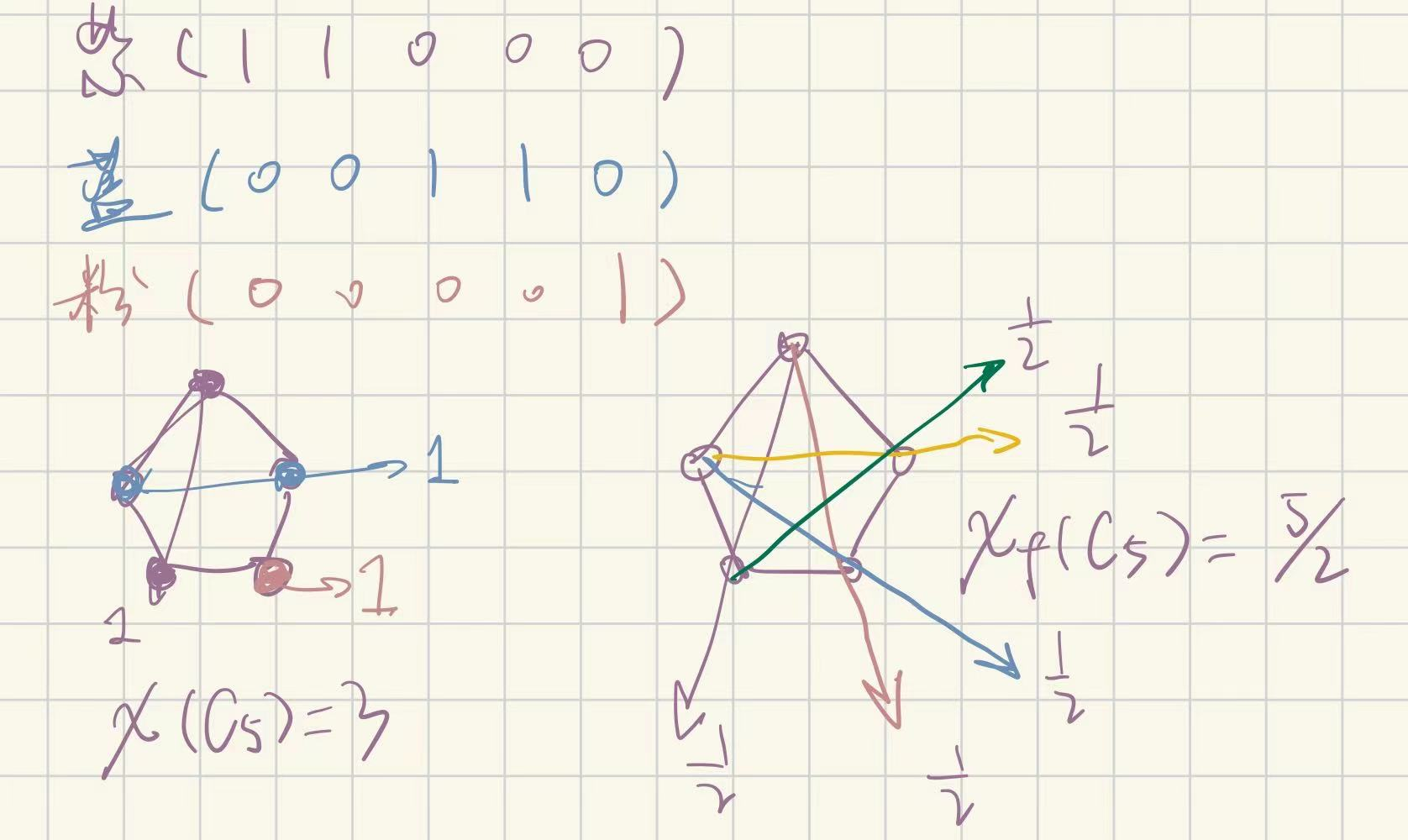
最后一个限制条件是向量限制条件（就有点像完备性那种），$1_{|V|}$是长度为$|V|$的全为1的向量；他的意思就是说每个颜色代表了一个由0，1组成的顶点向量，上这个颜色的顶点就写1，不上这个颜色的顶点就写0；然后你把所有颜色给的向量加起来，由于每个点都有且仅有一个着色，所以最后加起来就是个全1的向量

分数阶染色数

\[\chi_f(G)=\min\sum_{I\in I(G)}\lambda_I;\lambda_I\ge0,\sum_{I\in I(G)}\lambda_I\chi^I=1_{|V|}\]

跟传统的染色数相比每个点可以不专一了，可以分成两个心，染几个不同颜色，但是最后加起来每个点的总权重还是1；相邻两点没有任何重色现象

命题[2017]：设图G的染色数是$\chi(G)$,G的（可以带权）邻接矩阵中，有$n_+(G)$个正数特征值和$n_-(G)$个负数特征值（0特征不管了），则有

\[\chi(G)\ge1+max\{\frac{n_+(G)}{n_-(G)},\frac{n_-(G)}{n_+(G)}\}\]

引理：对一个染色数为k的图G，存在对角酉阵序列{$U_1,..,U_k$},使得对G的邻接矩阵A(G),有

\[\sum_{j=1}^{k-1}U_jA(G)U_j^\dagger=-A(G)\]

引理证明：对于k染色方案，先设每一种染色方案对应着一个实数，序号为x的点对应的染色对应的实数为c(x)

对角酉阵也就是说仅有对角线上存在模长为1的复数，我们这样构造一下第j个矩阵

\[(U_j)_{nm}=\delta_{nm}\exp(\frac{2\pi i}{k}jc(n))\]

也即，将k次单位根乘上矩阵编号乘上对应点染色c数

注意到$U_k=I$,故$U_kA(G)U_k^\dagger=A(G)$

现在考虑$U_jA(G)U_j^\dagger$的n行m列元素

\[(U_jA(G)U_j^\dagger)_{nm}=\exp(\frac{2\pi i}{k}jc(n))\lambda(n,m)\exp(-\frac{2\pi i}{k}jc(m))\]

其中，λ(n,m)是n到m边的权，无边时取0；对于这个元素进行分类讨论

1.λ(n,m)=0时，该分量始终为0，求和后也为0

2.λ(n,m)!=0时，意味着n，m之间有边，所以他们不可能被上同一种颜色，也即c(n)!=c(m)

\[\sum_{j=1}^kexp(\frac{2\pi i}{k}(c(n)-c(m))j)=0\]

故

\[\sum_{j=1}^{k}U_jA(G)U_j^\dagger=0\]

又因为$U_kA(G)U_k^\dagger=A(G)$，所以

\[\sum_{j=1}^{k-1}U_jA(G)U_j^\dagger=-A(G)\]

引理证毕，现在回到主线

对于实对称的邻接矩阵A(G),必可以对角化；现在将A(G)中正特征值及其特征向量拆分出来，记作B；将负特征值及特征向量拆出来并反号记作C

则A(G)=B-C；B、C半正定；将正特征对应的特征向量张成的空间对应的投影算符记作$P_+$，负特征对应$P_-$,则有$P_-P_+=0,P_+BP_+=B,P_+CP_+=0,P_-BP_-=0,…$

使用引理，对将要证明的图有这样的等式

\[\sum_{j=1}^{k-1}U_jA(G)U_j^\dagger=-A(G)\]

两边作用$P_-$并将A=B-C代入

\[\sum_{j=1}^{k-1}P_-U_j(B-C)U_j^\dagger P_-=P_-CP_--P_-BP_-=C\] \[\sum_{j=1}^{k-1}P_-U_jBU_j^\dagger P_--C=\sum_{j=1}^{k-1}P_-U_jCU_j^\dagger P_-\]

由于B、C半正定，故上式左侧两块半正定，右侧也半正定

引理2.对于半正定矩阵M1、M2，若M1-M2也是半正定，则有$rank(M_1)\ge rank(M_2)$

引理2证明：反证，若$rank(M_1)< rank(M_2)$,则$dimker(M_1)>dimker(M_2)$，此时$\exists x\ne 0,x\in ker(M_1),x\notin ker(M_2)$，将$M_1-M_2$作用在x上，得到$-M_2x<0$，矛盾，故原命题得证。

回到主线，我们根据引理2得到了

\[rank(\sum_{j=1}^{k-1}P_-U_jBU_j^\dagger P_-)\ge rank(C)\]

又因为

\[rank(\sum_{j=1}^{k-1}P_-U_jBU_j^\dagger P_-)\le \sum_{j=1}^{k-1}rank(P_-U_jBU_j^\dagger P_-)\le \sum_{j=1}^{k-1}rank(B)\]

带入后有

\[n_-\le(k-1)n_+\]

也即

\[k\ge 1+\frac{n_-}{n_+}\]

在上面对求和式同乘操作时，改同乘$P_+$后同理可得

\[k\ge 1+\frac{n_+}{n_-}\]

所以原命题得证

图同构

两个图同构体现在邻接矩阵上就是有一个置换矩阵P，使得$PA(G)P^{-1}=A(G’)$

那么分数阶图同构就是把上面的P置换矩阵放松到P双随机矩阵，矩阵元取值在[0,1]间

习题：证明分数阶图同构保总边数

引理：双随机矩阵P的逆$P^{-1}$保持左右映射均有不动向量$\vec 1$的特性

证明:

\[P^{-1}P\vec 1=P^{-1}\vec 1=\vec 1\] \[P^{-T}P^T\vec 1=P^{-T}\vec 1=\vec 1\]

习题的证明：首先我们可以将总边数写成二次型的形式，并记作相应的狄拉克符号

\[|E(G)|=\vec 1^TA(G)\vec 1=<1|A(G)|1>\]

而分数阶图同构的G’边数为

\[|E(G')|=<1|PA(G)P^{-1}|1>\]

用到引理，P逆仍然保持1向量不变，故

\[|E(G')|=<1|A(G)|1>=|E(G')|\]

好像没啥要证的，写一下IP2协议（新东西）交互式证明

以判断G1和G2是否图同构为例

A随机选择图G1或者图G2，并且对这个图施加一个置换，然后抛给M，问M：我这个操作过的新图和G1同构还是和G2同构？

这时候算力无穷的M会给你1~2中的一个回答

A可以多次调整自己手中的参数，给M不同问题；如果G1 G2是同构的，则M给你12回答是等概率的；如果不同构，那么M只会给你你先前选中的图编号。

随机游走

记号：A是带权邻接矩阵，D是对角矩阵，对角线上元素=对应点的带权度，L是拉普拉斯矩阵

习题：若图是连通非二部图，证明$D^{-\frac{1}{2}}AD^{-\frac{1}{2}}$的特征值从大到小依次是$1=\lambda_1>\lambda_2\ge…\ge\lambda_n> -1$

引理：拉普拉斯矩阵L=D-A是半正定的，最小特征值是0，特征0对应的特征向量是$\vec 1$。次小特征值非0<=>图连通

证明在图与邻接矩阵那一节

首先注意到A是实对称，所以$D^{-\frac{1}{2}}AD^{-\frac{1}{2}}$也是实对称的，也就是说特征数目足够。先证明$D^{-\frac{1}{2}}AD^{-\frac{1}{2}}$有1特征。将$\vec 1$是L的特征向量代入

\[L\vec 1=D\vec 1-A\vec 1=0\] \[A\vec 1=D\vec1\Rightarrow D^{-\frac{1}{2}}A\vec 1=D^{-\frac{1}{2}}D\vec1=D^{\frac{1}{2}}\vec1\] \[D^{-\frac{1}{2}}AD^{-\frac{1}{2}}D^{\frac{1}{2}}\vec 1=D^{\frac{1}{2}}\vec1\]

也即，$D^{\frac{1}{2}}\vec1$是$D^{-\frac{1}{2}}AD^{-\frac{1}{2}}$特征为1的特征向量

下面证明$D^{-\frac{1}{2}}AD^{-\frac{1}{2}}$没有大于1的特征，使用反证，假设$\ket{x}$是$D^{-\frac{1}{2}}AD^{-\frac{1}{2}}$特征大于1的特征向量，则有

\[\frac{<x|D^{-\frac{1}{2}}AD^{-\frac{1}{2}}|x>}{<x|x>}<1\Rightarrow\bra{x}I-D^{-\frac{1}{2}}AD^{-\frac{1}{2}}\ket{x}<0\] \[\bra{x}D^{-\frac{1}{2}}(D-A)D^{-\frac{1}{2}}\ket{x}<0\]

记$\ket{y}=D^{-\frac{1}{2}}\ket{x}$，则

\[\bra{y}L\ket{y}<0\]

这与L半正定矛盾，故$D^{-\frac{1}{2}}AD^{-\frac{1}{2}}$没有大于1的特征

引理：关于联通图的度矩阵与邻接矩阵的和K=A+D的性质

仿照拉普拉斯矩阵的二次型写法，可以将K的二次型$x^TKx$写作$\sum_{ij\in E}w_{ij}(x_i+x_j)^2$,所以K也是一个半正定矩阵，二次型取0<=>x是0特征对应的特征向量<=>$\forall ij\in E,x_i=-x_j$

在kerK中，若有一个xi分量取0，则与其相连的所有点也必须取0，由于连通性会导致全图取0，这是平凡的kerK空间向量。只考虑kerK空间中的非0向量x，此时x的所有分量都非0，故一条边相连的两个端点必然一正一负，这自然地将点利用x分量的正负性划分为两个部分，所以图一定是二部图

若图是二部图，直接取一侧xi=1，一侧xi=-1，代入二次型必然为0

也即K半正定，K有非平凡核空间当且仅当图是二部图

利用引理可以证明联通非二部图的$D^{-\frac{1}{2}}AD^{-\frac{1}{2}}$的最小特征值>-1

还是用反证，设非0向量$\ket{x}$满足$\bra{x}D^{-\frac{1}{2}}AD^{-\frac{1}{2}}\ket{x}\le-\braket{x|x}$

则有$\bra{D^{-\frac{1}{2}} x}A+D\ket{D^{-\frac{1}{2}} x}\le0$，这与联通非二部图的K=A+D正定矛盾，故$D^{-\frac{1}{2}}AD^{-\frac{1}{2}}$的最小特征值>-1（本习题证毕）

利用上面的习题证明图G上的随机游走具有遍历性(不计初始状态地收敛到同一个不动状态)<=>G联通且非二部

稳定分布：转移矩阵$AD^{-1}$满足$AD^{-1}=D^{\frac{1}{2}}D^{-\frac{1}{2}}AD^{-\frac{1}{2}}D^{-\frac{1}{2}}\Rightarrow AD^{-1}\sim D^{-\frac{1}{2}}AD^{-\frac{1}{2}}$，所以转移矩阵与$D^{-\frac{1}{2}}AD^{-\frac{1}{2}}$同谱，则必有特征1，特征1空间中的某个向量$\pi$满足概率诠释（$\pi·\vec 1=1$）

\[AD^{-1}\pi=\pi\]

这个不动点（不动状态）其实是已知的了。在习题中证明了$D^{\frac{1}{2}}\vec1$是$D^{-\frac{1}{2}}AD^{-\frac{1}{2}}$特征为1的特征向量，则由相似关系，$D\vec 1$是转移矩阵$AD^{-1}$特征为1的特征向量，故$\pi=\frac{1}{\sum d}D\vec 1$,$\sum d$是全顶点带权度和

先证明充分性，用反证。对于一个非连通图，假设有不相连的区域A、B，则从A出发无论怎么走都还是在A内，从B出发也会在B内，他们肯定不会收敛到同一个末态；对于二部图，走t次位于哪里完全取决于t的奇偶性，奇数t和偶数t的末态一定不同，所以不会收敛到某个不动点。

再证明必要性：设$D^{-\frac{1}{2}}AD^{-\frac{1}{2}}$的特征向量组是{$\vec x$}（由于实对称所以完备），那么$AD^{-1}$的完备特征向量组为{$\vec y=D^{\frac{1}{2}}\vec x$}

设任意初始状态$\vec p_0$,在$AD^{-1}$表象下展开有

\[\vec p_0=\sum_{i=1}^n c_i\vec y_i\]

其中，特征向量y的编号与特征编号（从大到小）一致。游走t步后的概率分布为

\[(AD^{-1})^t\vec p_0=\sum_{i=1}^n \lambda_i^tc_i\vec y_i\]

令$t\to\infty$，由于λ2~λn的绝对值<1，所以他们会收敛到0，只剩下第一项

\[\lim_{t\to\infty}(AD^{-1})^t\vec p_0=c_1\vec y_1\]

$c_1\vec y_1$与$\pi$都是$AD^{-1}$特征为1的特征向量，且特征1非简并，故这两个向量共线；另一方面，$\pi$满足$\pi·\vec 1=1$，而$AD^{-1}$是列归一矩阵，必定会将满足概率诠释的状态向量映到一个也概率诠释的状态向量上，自$\vec p_0$作用∞次后得到的$c_1\vec y_1$也会满足$c_1\vec y_1·\vec 1=1$。

有了这个限制条件后可以断言，无论初始状态p0如何，随机游走无穷次后一定收敛到不动状态$\pi=\frac{1}{\sum d}D\vec 1$

有向图随机游走遍历性条件：强连通且环长度互素

其中用到的引理(Perron-Frobenius定理)：列归一的不可约递归矩阵$AD^{-1}$（不可置换分块对角化）的谱半径恰为一个特征值，且对应的左右特征空间均非简并

证明抄自wiki

Given a strictly positive eigenvector v corresponding to r and another eigenvector w with the same eigenvalue. (The vectors v and w can be chosen to be real, because A and r are both real, so the null space of A-r has a basis consisting of real vectors.) Assuming at least one of the components of w is positive (otherwise multiply w by −1). Given maximal possible α such that u=v- α w is non-negative, then one of the components of u is zero, otherwise α is not maximum. Vector u is an eigenvector. It is non-negative, hence by the lemma described in the previous section non-negativity implies strict positivity for any eigenvector. On the other hand, as above at least one component of u is zero. The contradiction implies that w does not exist.

然后我们又已知最大模对应的特征值为1，他有且仅有左特征向量$\vec 1^T$，也就是说$\vec x^TAD^{-1}=\vec x^T\Rightarrow\vec x^T=c\vec 1^T$

布尔函数敏感度

多项式表示布尔函数：定义域只是很多个F2，所以由于$x_i^n=x_i$可以直接降次至多项式分别对每个变量线性

习题：证明任何布尔函数存在唯一的多线性多项式表示

证明：假设$f_1$与$f_2$都是某个布尔函数的多线性多项式表示，则$f_1-f_2$也是多线性多项式，且对于任意的一组自变量取值，结果都是0

不妨设$f_1-f_2$中显含布尔变量$x_i$（如果什么都不显含，那$f_1=f_2$证毕），固定其他变量，此时$(f_1-f_2)(x_i)$是线性函数，线性函数只可能有一个0点，所以不满足对于$x_i$取0或1结果都是0

故任何布尔函数存在唯一的多线性多项式表示

\[s(f,x)=|\{i:f(x)\neq f(x\oplus i)\}|\]

对于一个确定的布尔函数f及当前取值，反转第i个x后函数值发生变化，并数出这种i有多少个，这就是s

敏感度就是取遍所有的当前自变量值x，找到最大的s

AND的敏感度：在1and1时，无论反转哪个都会改变函数值，所以敏感度为2，OR函数同理，不过是在0OR0处取得敏感度2

超立方体图中导出子图的最大度

这是秒发Annals的证明，而且借助图论直接能说明布尔函数的决策树、块敏感度、敏感度等度量是多项式等价的，太帅啦！

超立方体图$Q^n$：直观上来看就是你把上一个图copy paste一份，然后自己与自己的副本相连。你想下比如说一个正方形，复制粘贴，连四个顶点，就可以成为一个立方体。从数学上来看，n阶超立方体图就是遍历生成长度n的01串，总共就有2^n个顶点；其中汉明距离=1<=>有边

导出子图最大度Δ(H):子图中顶点的最大度（有最多手的顶点的手的个数）

定理[黄皓，2019]:对$Q^n$中的任意导出子图H,若$|V(H)|>2^{n-1}$,则$\Delta(H)>\sqrt{n}$

引理：对任意图G([n],E)，有$\Delta(G)\ge\lambda_{max}(A_G’)$,其中$A_G’$是符号邻接矩阵，满足对所有分量取绝对值后构成的矩阵为邻接矩阵（也即原先有1的分量也可以填-1）

引理证明：对$\lambda_{max}(A_G’)$对应的特征向量$\vec v$，我们总可以调整长度使得其绝对值最大的分量为1，记作$v_i=1$，则有$\forall j\in{1,2,…,n},v_j\in[-1,1]$

则

\[\lambda_{max}=\lambda_{max}v_i=(A_G\vec v)_i=(A_G)_i^{~j}v_j\le|(A_G)_i^{~j}|·|v_j|\le\sum_j|(A_G)_i^{~j}|\le\Delta(G)\]

故引理成立

main证明：

先展示一下$Q^n$的传统邻接矩阵序列
\[A_{Q^1}=\begin{pmatrix} 0&1\\ 1&0\\ \end{pmatrix};~~~~A_{Q^n}=\begin{pmatrix} A_{Q^{n-1}}&I_{2^{n-1}}\\ I_{2^{n-1}}&A_{Q^{n-1}}\\ \end{pmatrix}\]
习题：$𝐴_{𝑄^𝑛}$的特征值序列是$(−𝑛,−𝑛+2,…,𝑛−2,𝑛)$，第𝑘大特征值的重数是nCk

习题证明：用归纳法，当n=1时邻接矩阵有特征值序列(-1,1),重数均为1C0=1C1=1

假设命题在<n时成立，下面证明在n时成立。设长度为2^n的特征向量由上面一个长度为$2^{n-1}$的向量$\vec a$与下面一个长度为$2^{n-1}$的向量$\vec b$拼成，即
\[\vec v=\begin{pmatrix} \vec a\\ \vec b\\ \end{pmatrix}\]
注意到
\[A_{Q^n}=\begin{pmatrix} A_{Q^{n-1}}&O\\ O&A_{Q^{n-1}}\\ \end{pmatrix}+\begin{pmatrix} O&I_{2^{n-1}}\\ I_{2^{n-1}}&O\\ \end{pmatrix}\]
若$\vec a$与$\vec b$同属$A_{Q^{n-1}}$特征为λ的特征向量，则有
\[A_{Q^n}\vec v=\begin{pmatrix} A_{Q^{n-1}}&O\\ O&A_{Q^{n-1}}\\ \end{pmatrix}\begin{pmatrix} \vec a\\ \vec b\\ \end{pmatrix}+\begin{pmatrix} O&I_{2^{n-1}}\\ I_{2^{n-1}}&O\\ \end{pmatrix}\begin{pmatrix} \vec a\\ \vec b\\ \end{pmatrix}=\begin{pmatrix} \lambda\vec a+\vec b\\ \lambda\vec b+\vec a\\ \end{pmatrix}\]
若v是$A_{Q^n}$特征为μ的特征向量，则
\[\lambda\vec a+\vec b=\mu\vec a\] \[\lambda\vec b+\vec a=\mu\vec b\]
由a，b不为0可得
\[\mu=\lambda+ 1,a=b\]
or
\[\mu=\lambda- 1,a=-b\]
也即，对$A_{Q^{n-1}}$中的一条特征为λ的向量a，可以生成一个$A_{Q^{n}}$中的特征为λ+1的特征向量(a;a)以及特征为λ-1的特征向量(a;-a)；由短无关则长无关可知，遍历k个线性无关的a可以生成$A_{Q^{n}}$中2k个线性无关的向量

而由归纳假设，$𝐴_{𝑄^{𝑛-1}}$的特征值序列是(−𝑛+1,−𝑛+3,…,𝑛−3,𝑛-1)，第𝑘大特征值的重数是(n-1)Ck

故$𝐴_{𝑄^{𝑛}}$至少有特征序列(−𝑛,−𝑛+2,…,𝑛−2,𝑛)，第𝑘大特征值的重数是$C_{n-1}^{k-1}+C_{n-1}^k=C_n^k$，原命题得证

对于$Q^n$，按如下递推的方式生成符号邻接矩阵$A_{Q^n}’$

\[A_{Q^1}'=\begin{pmatrix} 0&1\\ 1&0\\ \end{pmatrix};~~~~A_{Q^n}'=\begin{pmatrix} A_{Q^{n-1}}&I_{2^{n-1}}\\ I_{2^{n-1}}&-A_{Q^{n-1}}\\ \end{pmatrix}\]

注意到$A_{Q^n}’^2=nI$(证明(归纳)：$A_{Q^1}’^2=I,A_{Q^n}’$=(A^2+I,0;0,A^2+I)=nI),所以$A_{Q^n}’^2$仅有特征n，所以$A_{Q^n}’$仅有特征$\pm\sqrt{n}$

注意到$tr(A_{Q^n}’)=0$，故$A_{Q^n}’$的两个特征$\pm\sqrt{n}$重数均为$2^{n-1}$

由柯西交错定理：令$λ_i$代表第i大特征值，B(mxm)是A(nxn)的主子阵，则$\lambda_{n-m+i}(A)\le\lambda_i(B)\le\lambda_i(A)$

在这里，$Q^n$中阶为$2^{n-1}+1$的导出子图对应原符号邻接矩阵的$2^{n-1}+1$阶主子阵，在柯西交错定理中表现为导出子图的符号邻接矩阵最大特征值$\ge\lambda_{2^{n-1}}(A_{Q^n}’)=\sqrt{n}$

再用一下最开始的引理，可得

\[\Delta(H)\ge\sqrt{n}\]

证毕

极值图论

这节课讲了关于极值图论奠基性的几个定理。极值图论研究的方向（之一）是：当V个顶点的图包含指定子图时，至少要连多少边，以及衍生的问题

Ramsey定理：对于六个顶点的图，要么出现三角形，要么出现三个点使得他们之间没有边相连

证明：

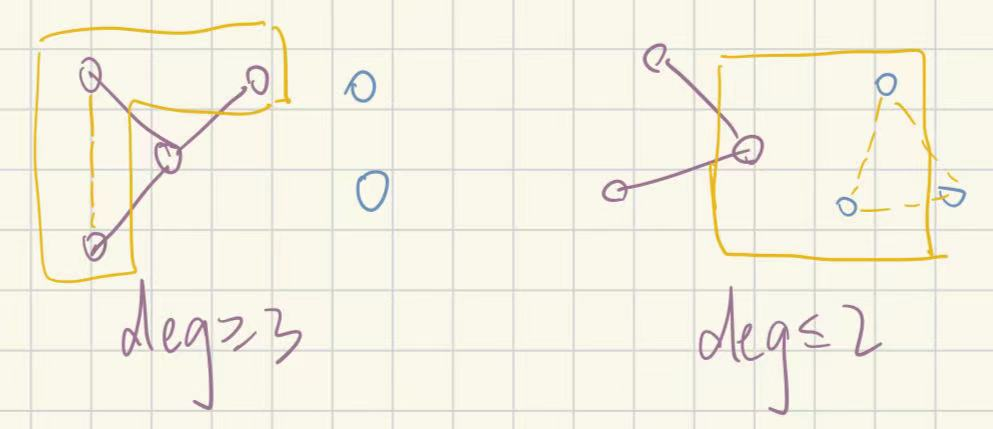
任取一个点并按其度分类，若deg不低于3，则图如左侧，若选中的这个点的邻居有相连则构成三角形，若无边相连则构成3-独立集

若deg不超过2，则去看他的补集（蓝色），若补集三条边全连上则有三角形不用说了，如果有哪条边没连，说明有2-独立集，再加上我们选中的那个顶点，构成了3-独立集

Mantel定理：不包含三角形的n个顶点的图最多有$n^2/4$条边

证明：

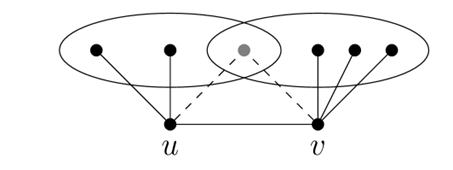
任取一条边上的两个顶点uv，观察u和v向别的点连出的边，由于不存在三角形，所以和u相连的点不会再和v相连，所以uv至多和n-2个顶点相连，也即

\[degu-1+degv-1\le n-2\Rightarrow degu+degv\le n\]

对所有的边的两端点求和，有

\[\sum_{uv\in E}degu+degv\le n|E|\]

并且注意到等式左边这个求和，对于某个顶点，他参加求和的次数恰为所参与的边个数，也就是度；每次求和加的数字也是个度，所以每个顶点贡献了他的度的平方，也即

\[\sum_{uv\in E}degu+degv\le \sum_{v\in V}deg^2(v)\]

代入，并利用柯西不等式可得上界

\[|E|n^2=n(\sum_{uv\in E}degu+degv)=n\sum_{v\in V}deg^2(v)=(\sum_V 1)(\sum_{v\in V}deg^2(v))\ge(\sum_{v\in V}deg(v))^2\]

而所有度求和一定是两倍边数，$\sum degv=2|E|$，故有

\[|E|\le\frac{n^2}{4}\]

完全图：所有能连的边都给连上了

Turán定理：不包含r顶点完全图的n个顶点的图至多有$\frac{(r-2)n^2}{2(r-1)}$条边

取r=3，退化到Mantel定理

证明：使用归纳法，当n不超过r-1时，$\frac{(r-2)n^2}{2(r-1)}$不超过$C_n^2$，恒成立

假设定理在$n\le N-1$时成立，考虑n=N

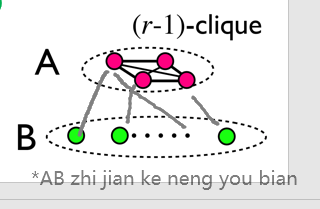
***输入法关键时刻没了；↑AB之间可能有边

在极限情况下会出现r-1团（完全图），我们把它分出去，如图分为A和B（不止一个r-1团，所以B中不保证有没有r-1团），但是这么操作使得B的顶点变少了以便可以使用归纳假设

对B，无r-团，使用归纳假设

\[|E(B)|\le\frac{r-2}{2(r-1)}(N-r+1)^2\]

这个图的边由三部分组成：B中边、B与A中边、A中边，所以说

\[\begin{aligned} |E|&\le\frac{r-2}{2(r-1)}(N-r+1)^2+(r-2)(N-r+1)+C_{r-1}^2\\ &=\frac{r-2}{2(r-1)}((N-r+1)^2+2(r-1)(N-r+1)+(r-1)^2)=\frac{(r-2)}{2(r-1)}N^2 \end{aligned}\]

刚刚好，这可真是太帅啦

由归纳假设知原命题成立

图论与整数

van der Waerden定理：对正整数集进行有限划分，其中必有一个集合存在任意长度的等差数列

整数子集A的上密度：

\[A\subset Z,\pi(A)=\limsup_{N\to \infty}\frac{|A\cap \{N,...,N\}|}{2N+1}\]

Erdos-Turan猜想:如果$\pi(A)>0$,则A中存在任意长的等差数列

只证明他的弱化版(Roth定理)：如果$\pi(A)>0$,则A中存在长度3的等差数列

证明：Szemeredi正则化定理（纯组合证明）

Roth定理等价于：若{-N,…,N}的子集A不包含长度为3的等差列，则$|A|=o(N)$(也即N的低阶无穷大，这样取极限的时候上密度就是0了)

图论刻画：每条边都包含在唯一一个三角形中的n顶点图的最大边数为$o(N^2)$

证明图论刻画的充分性：

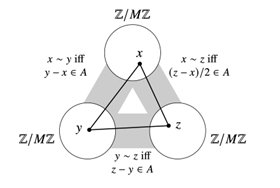
令M=2N+1（恰为A所在集合的大小），则A可以嵌入至Z/MZ中而不改变A的结构

构造三方图，使得每一部分的顶点代表着Z/MZ中的元素，连边规则为

XY间有边$\iff y-x \in A$

XZ间有边$\iff (z-x)/2 \in A$

YZ间有边$\iff z-y \in A$

注意到(y-x+z-y)/2=(z-x)/2，用作判定的三个数字如果全在A内则恰给出A内的一组3-等差数列，但是条件是A中没有非平凡的等差列，所以这三个数在A中是同一个，也即y-x=(z-x)/2=z-y(换一种说法就是A中每个元素拉出该图的一个三角形)，所以G中每条边包含在唯一三角形中

下面数数G中有多少边，3MA=3(2N+1)*A,如果图论刻画正确，则$|A|=o(N)$

定义边密度：对于图G的顶点子集X和Y，XY的边密度定义为

\[d_G(X,Y)=\frac{e_G(X,Y)}{|X||Y|}\]

也就是XY之间的桥梁除XY大小，或者说随便挑一对(x,y)，他们之间有边的概率

ε-正则对(U,W):U,W是图G的顶点子集，使得所有满足$|A|≥ε|U|$与$|B|≥ε|W|$且A是U的子集，B是W的子集的集合A，B均满足$|d(A,B)=d(U,W)|≤\epsilon$

也即在U，V中任意不太小的两个子集，之间的桥梁密度和大集合之间的桥梁密度很相近；他反应的是UV之间桥梁分布的均匀性，分布得越不均匀，ε只能越大越靠近1

ε-正则划分：顶点集合的划分{V1,…,Vk}满足所有非ε-正则对的大小积的和有上界$\epsilon|V|^2$(总顶点数)，写出来就是

\[\sum_{(V_i,V_j)\notin\varepsilon-regularity}|V_i||V_j|\le\varepsilon|V|^2\]

Szemerédi正则性引理：对于任意𝜀>0，存在常数𝑀，使得每个图的顶点集可以被𝜀-正则划分为𝑀个部分（𝑀与顶点数无关）

实际上这个M会很大，但是无所谓，我们这一节探讨的是图在∞方向上的渐进行为

其实这个也好理解，正则对意思就是这两个集合之间的桥梁密度还比较均匀，那么不均匀怎么办呢？把大密度和小密度再分开就好了，这样直观上来看确实会让划分越来越靠近正则

正则性引理的证明就是如此，利用非正则的部分继续细分；或者换言之也像模拟退火或者找函数局部最优，也是通过算梯度得到下一步怎么走会更优化，然后一步步靠近最优

现在用一个东西标度两个顶点子集之间的能量：$q(U,W)=\frac{|U||W|}{n^2}d(U,W)^2=\frac{e(U,W)^2}{n^2}$

子集pair划分之间的能量：$P_U={U_1,…,U_k},P_W={W_1,…,W_k},q(P_U,P_W)=\sum_{ij}q(U_i,W_j)$

引理：对于U，W的划分$P_U,P_W$,有$q(P_U,P_W)\ge q(U,W)$

证明：(概率证明)均匀随机选取$x\in U,y\in W$,并找到(x,y)所在的划分Ui，Wj(则选中这一对划分元素对的概率为$\frac{|U_i||W_j|}{|U||W|}$)，考虑随机变量z=d(Ui,Wj)，计算其1、2阶矩

\[<z>=\sum_{ij}\frac{|U_i||W_j|}{|U||W|}d(U_i,W_j)=\sum_{ij}\frac{e(U_i,W_j)}{|U||W|}=d(U,W)=\sqrt{\frac{n^2}{|U||W|}q(U,W)}\] \[<z^2>=\sum_{ij}\frac{|U_i||W_j|}{|U||W|}d(U_i,W_j)^2=\sum_{ij}\frac{n^2}{|U||W|}q(U_i,W_j)=\frac{n^2}{|U||W|}q(P_U,P_W)\]

由$\braket{z^2}\ge\braket{z}^2$知原命题得证(也就是说细分会增大能量，下面来定量分析增加了多少)，考虑U，W不是ε-正则对的情况，此时存在子集A，B满足$|d(A,B)-d(U,W)|>\varepsilon$,现在把U，W分别切一刀，把A，B切出去，形成划分$P_U,P_W$

还是玩上面那个随机变量z

\[\sigma(z)=\braket{z^2}-\braket{z}^2=\frac{n^2}{|U||W|}(q(P_U,P_W)-q(U,W))\]

另一方面

\[\sigma(z)=\braket{(z-\braket{z})^2}\]

而z代表d(Ui,Wj)，代表d(U,W)，他们之间的差可以用非正则的特性给出与ε相关的下界

\[\sigma(z)\ge\frac{|A||B|}{|U||W|}\varepsilon^2>\varepsilon^4\]

所以把A，B切出去，形成划分$P_U,P_W$，增加能量

\[q(P_U,P_W)>q(U,W)+\frac{|U||W|}{n^2}\varepsilon^4\]

下面考虑自身到自身上的能量与划分，q(U):=q(U,U).如果V现有的k-划分{Vi}非正则，则一定是因为有一些Vi到Vj之间的桥非正则(密度不均)，那么还是像之前一样将密度不均的部分(A,B)细分出去

对一个子集Vi,最多能找到k+1个不正则的子集A，他们将Vi细分为至多$2^{k+1}$个

下面计算细分后的能量增量

\[\sum_{(i,j)\notin regular}q(P_i'-P_j')-q(V_i,V_j)\ge\sum_{(i,j)\notin regular}\frac{|V_i||V_j|}{n^2}\varepsilon^4\ge\varepsilon^5\]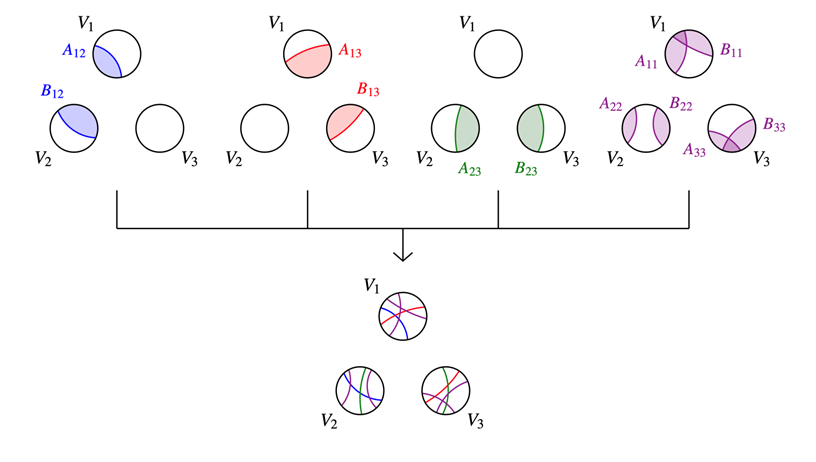

上图表示：找到非正则部分->细分的过程

综上，每次细分至少增加$\varepsilon^5$能量，而总能量有上界1，所以至多进行$\varepsilon^{-5}$次迭代就可以做到正则化；并且每一次划分增加部分的上界是$2^{2^k}$，与图参数无关，所以我们证明了Szemerédi正则性引理

𝜀-正则对的作用：在一个𝜀-正则对(X,Y)中，如果有某个子集$A\subset X$到Y的桥梁密度与总桥梁密度相差太大，那么一定是因为A太小了，即$|A|<\varepsilon|X|$；我们把这句陈述换个形式写出来

\[d(A,Y)<d(X,Y)-\varepsilon=\frac{|A|(d(X,Y)-\varepsilon)|Y|}{|A||Y|}\] \[\frac{e(A,Y)}{|A|}<(d(X,Y)-\varepsilon)|Y|\]

现在给上面的等式找一个较强的充分条件，记A直接连到Y中的点构成的子集为N(A)（也就是A在Y中的邻居构成的子集），那么$N(A)\ge e(A,Y)/|A|$（左侧或右侧只有一个端点时取等）

上式的充分条件为

\[N(A)<(d(X,Y)-\varepsilon)|Y|\]

脱离A，我们直接将该推论写作𝜀-正则对(X,Y)满足

\[|\{x\in X:|N(x)\cap Y|<(d(X,Y)-\varepsilon)|Y|\}|<\varepsilon|X|\]

也就是说不满足冒号后面那个条件的x的数目有上界

推论：三角形计数引理：XYZ两两正则，则由XYZ各出一个顶点构成的三角形个数$≥(1-2\epsilon)(d(X,Y)-\epsilon)(d(X,Z)-\epsilon)(d(Z,Y)-\epsilon)|X||Y||Z|$

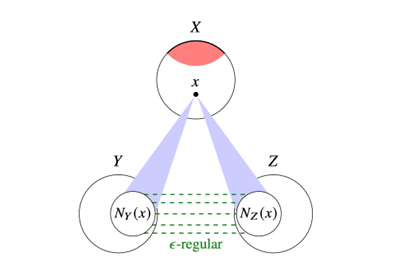
证明：使用引理，现在我们想排除那些不满足“冒号后面条件”的x，这些x最多有𝜀|X|个，所以我们可以取子集$X’\subset X,s.t.|X’|>(1-2\varepsilon)|X|$，使得X’中的任意点均满足反“冒号后面条件”，也即

\[N_Y(x)\ge\varepsilon|Y|;N_Z(x)\ge\varepsilon|Z|\]

这个大于号正好给了我们两个子集去用正则化条件，所以$|d(N_Y(x),N_Y(x))-d(Y,Z)|\le\varepsilon$

所以x两个邻居之间的边数可以给个下界

\[d(N_Y(x),N_Z(x))|N_Y(x)||N_Z(x)|\ge|Y||Z|\Pi_{cyc}(d(X,Y)-\varepsilon)\]

三角形移除引理：对任意𝜀>0，存在𝛿>0满足若𝑛个顶点的图𝐺中只有不超过𝛿𝑛^3个三角形，那么可以通过删除不超过𝜀𝑛^2条边来保证𝐺中没有三角形

证明：由正则性引理，可以找到𝜀/4-正则划分V1,…,Vm，现在先删除这些边

1.(Vi,Vj)不是𝜀/4-正则(至多删除𝜀𝑛^2/4)

2.d(Vi,Vj)<𝜀/2(至多删除𝜀𝑛^2/2)

3.Min{|Vi|,|Vj|}<𝜀𝑛/4𝑚(至多删除𝜀𝑛^2/4)

(至多删除𝜀𝑛^2条边)那么如果删了之后还存在三角形，则由三角形计数原理，三角形数目不小于$(1−\frac{\varepsilon}{2}) (\frac{\varepsilon}{4})^3 (\frac{\varepsilon n}{4m})^3$,与条件矛盾，故删除后没有三角形了

推论：每条边都包含在一个唯一三角形中的 𝑛 顶点图的最大边数𝑜(𝑛^2)

证明：记边数为𝑚，由每条边都包含在唯一三角形中可知图中三角形的数目是𝑚/3≪𝑛^3

由三角形移除引理，只需移除𝑜(𝑛^2)条边将其中的所有三角形破坏

删除一条边只能破坏一个三角形，故删除的边数恰好是三角形个数，m/3=o(n^2)

有了这么漫长的组合图论证明后，终于得到了Roth定理成立！

Erdos-Turan猜想推论：由素数定理$\pi(x)\sim\frac{x}{lnx}$(其实你也可以用切比雪夫定理估算出$\pi(n)\ge\frac{ln2}{3}\frac{n}{lnn}$给个下界就足够了)，所以可以知道素数内有任意长等差列

已完结！

线代：学好之后，本科不愁

第一节课的预告

实际上讲的

参考

1.https://zhuanlan.zhihu.com/p/624504204

原创文章转载请注明出处: 图论笔记

新手产生的图论入门级代码堆以及相关性质证明

经典P与NP问题

图与邻接矩阵

最小割最大流

最大割

扩展图

匹配与覆盖

独立数与香农容量

染色数

图同构

随机游走

布尔函数敏感度

极值图论

图论与整数

Share on: