流体力学基础：从本构方程到NS方程

开个坑，因为感觉这一条线的推导是流体力学中很基础的理论线，所以想自己走一遍

抄书：周光坰《流体力学》

组成：应变率张量与应力张量

对于研究的目标流体，有流速场$\vec V(\vec x)$,下面我们在直角坐标系下研究，设流速的x、y、z分量分别为$u(x,y,z),v(x,y,z),w(x,y,z)$

分别对这三个方向上的速度值求梯度，可以得到这样的张量（矩阵形式）

\[\frac{\partial v^i}{\partial x^j} =\begin{pmatrix} \frac{\partial u}{\partial x}&\frac{\partial u}{\partial y}&\frac{\partial u}{\partial z}\\ \frac{\partial v}{\partial x}&\frac{\partial v}{\partial y}&\frac{\partial v}{\partial z}\\ \frac{\partial w}{\partial x}&\frac{\partial w}{\partial y}&\frac{\partial w}{\partial z} \end{pmatrix}\]

注意到这个矩阵满足的性质：左作用在位移dx上得到dv
\[\begin{pmatrix} du\\ dv\\ dw \end{pmatrix}=\begin{pmatrix} \frac{\partial u}{\partial x}&\frac{\partial u}{\partial y}&\frac{\partial u}{\partial z}\\ \frac{\partial v}{\partial x}&\frac{\partial v}{\partial y}&\frac{\partial v}{\partial z}\\ \frac{\partial w}{\partial x}&\frac{\partial w}{\partial y}&\frac{\partial w}{\partial z} \end{pmatrix}\begin{pmatrix} dx\\ dy\\ dz \end{pmatrix}\]

现在将这个矩阵分解为对称部分S和反对称部分

\[\begin{pmatrix} \frac{\partial u}{\partial x}&\frac{\partial u}{\partial y}&\frac{\partial u}{\partial z}\\ \frac{\partial v}{\partial x}&\frac{\partial v}{\partial y}&\frac{\partial v}{\partial z}\\ \frac{\partial w}{\partial x}&\frac{\partial w}{\partial y}&\frac{\partial w}{\partial z} \end{pmatrix}=S+A\] \[S=\begin{pmatrix} \frac{\partial u}{\partial x}&\frac{1}{2}(\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x})&\frac{1}{2}(\frac{\partial u}{\partial z}+\frac{\partial w}{\partial x})\\ \frac{1}{2}(\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x})&\frac{\partial v}{\partial y}&\frac{1}{2}(\frac{\partial v}{\partial z}+\frac{\partial w}{\partial y})\\ \frac{1}{2}(\frac{\partial u}{\partial z}+\frac{\partial w}{\partial x})&\frac{1}{2}(\frac{\partial v}{\partial z}+\frac{\partial w}{\partial y})&\frac{\partial w}{\partial z} \end{pmatrix}\] \[A=\begin{pmatrix} 0&\frac{1}{2}(\frac{\partial u}{\partial y}-\frac{\partial v}{\partial x})&\frac{1}{2}(\frac{\partial u}{\partial z}-\frac{\partial w}{\partial x})\\ \frac{1}{2}(\frac{\partial v}{\partial x}-\frac{\partial u}{\partial y})&0&\frac{1}{2}(\frac{\partial v}{\partial z}-\frac{\partial w}{\partial y})\\ \frac{1}{2}(\frac{\partial w}{\partial x}-\frac{\partial u}{\partial z})&\frac{1}{2}(\frac{\partial w}{\partial y}-\frac{\partial v}{\partial z})&0 \end{pmatrix}\]

S被称作应变率张量；A中的三个分量恰为1/2倍的旋度，Adx=Ωdx=w x dx,这一部分是绕瞬时轴转动时的速度

在下面的推导中，主要关注对称（无旋）速度场梯度S

作用在流体上的力分为表面力与场力，后者按密度均匀分配（比如重力），比较好理解，主要还是看表面力（也叫应力）

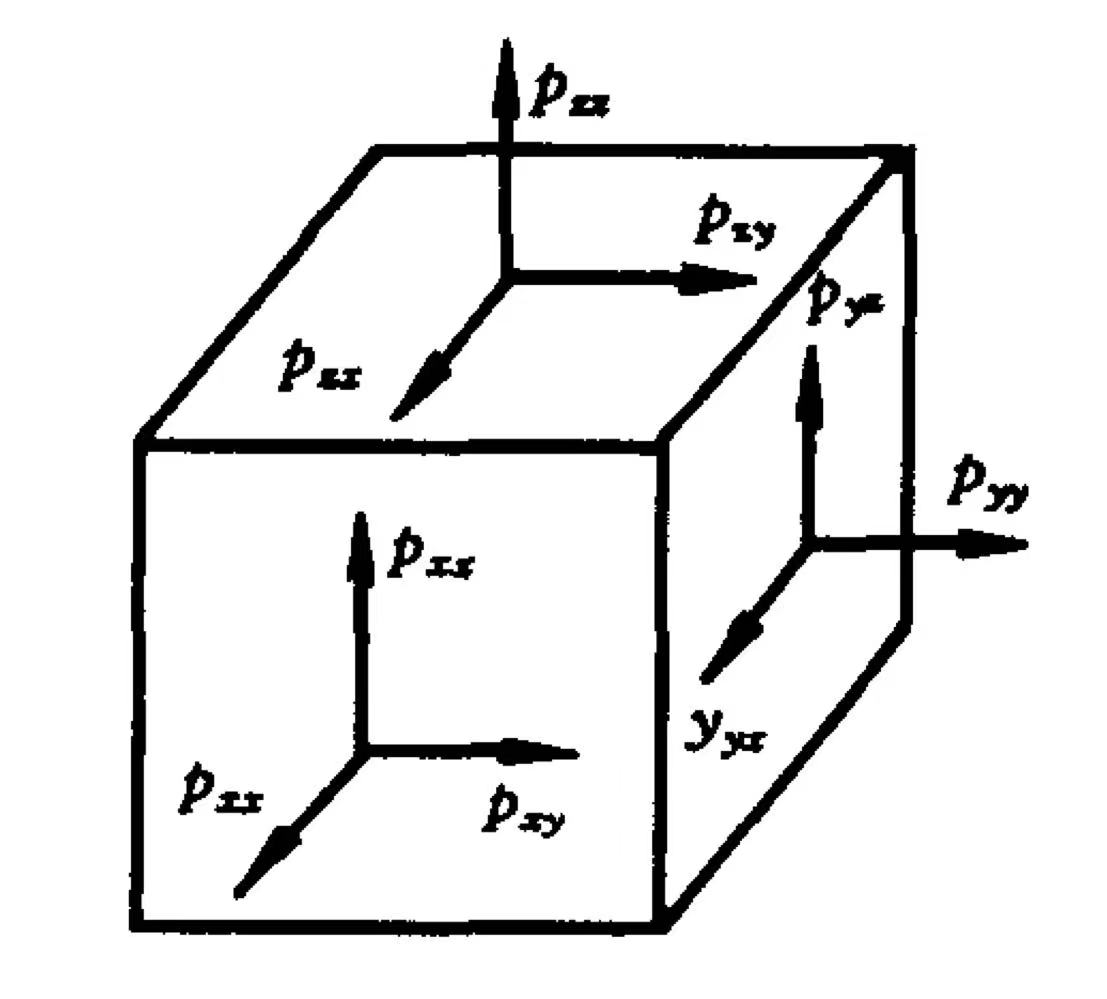
在体积微元dxdydz上，一共有三个面的力，每个面受力又分三个方向，所以总共就是3x3的矩阵来描述

\[P=\begin{pmatrix} p_{xx}&p_{xy}&p_{xz}\\ p_{yx}&p_{yy}&p_{yz}\\ p_{zx}&p_{zz}&p_{zz}\\ \end{pmatrix}\]

其中，pij代表i面上受到的j方向上的力；已知面的法向单位向量n求受力，就直接$\vec n^TP$即可

定理：应力张量P是对称的

证明：（关键在于观察无穷小的阶数）由于考虑的体积元很小，质量是三阶无穷小量，Δp是一阶小量，S是二阶小量，所以合外力ΔF是3阶小量，与质量同阶，可以存在；但是合力矩是三阶小量，转动惯量是五阶小量，所以在微元上必须有合力矩为0

能产生合力矩的只有交叉项，而力矩共线（能互相抵消）的只有对称项，例如$p_{xy}$、$p_{yx}$，他们产生的力矩正好共线反向，所以全部交叉对称项必然相等，也即P是对称的

对于理想的无粘性流体，P退化为压强标量

牛顿定律->本构方程

这一节书上的推导不是很令人满意的，遂查阅资料后写了一份适合自己思路的推导；只能保证结果是对的，如果你觉得我这个不合你胃口建议去看书

牛顿所得到的实验定律：流体间的切应力与速度梯度成正比,因子为粘度系数

\[\tau = \mu\frac{\partial u}{\partial y}\]

这个式子反映了应力P交叉项与流速梯度交叉项之间的关系

(P是对称的，所以在等式中只能先将速度梯度的反对称部分A不研究)为了半推半猜出张量P与张量S之间的关系，需要如下三个假设

1中其实包含了个前提假设，我在这里说清楚了：P由各向同性部分（I的倍数，无论如何转动都保持不变）与方向性部分组成，其中方向性部分被称作偏应力张量T

1.偏应力张量T与S成线性齐次关系(T=标量·S)

2.流体各向同性

3.静止流体（S=0）应力P退化到静压强

将1的前提假设与假设3联系起来，可以看出各向同性部分分为与S无关的静压力部分$p_0I$和动态部分$d(S)I$，则暂时可以将P写作

\[P=p_0I+d(S)I+T\]

使用假设1；注意到P的1，2项为$p_{xy}$；S的1，2项为$\frac{1}{2}(\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x})$，结合牛顿实验定律与假设2来推广，可得

\[T=2\mu S\]

实际上我觉得$p_{xy}$与$\frac{\partial v}{\partial x}$有关，$p_{yx}$与$\frac{\partial u}{\partial y}$有关，但是由于先前的微元不受合力矩导致交叉项全部混为一谈了

为了求出d(S)，仅需观察等式左右对角线上分量性质，所以求个迹（还有个原因，标量b是基无关的，求迹的好处是脱离基相关性）

\[p_{xx}+p_{yy}+p_{zz}=3p_0+3d(S)+2\mu\nabla\cdot\vec v\]

d(S)一定是关于S的基变换不变量，现在只可能和两种相关：{detS,trS}，考虑detS，若xyz中任意方向流速均匀，则detS=0，无法反映速度相关性质，所以仅取trS，也即divv,设

\[d(S)=\lambda\nabla·\vec v\]

其中，$\lambda$被称为体膨胀粘度系数，也被称为第二粘度系数；他反应了流体实际压强与流体的膨胀或压缩有关的性质。

这一段也是靠猜的

在最后的表达式中，为了与流行的写法一致，将静压强取一个负号，令p=-p0，最后得出本构方程，P关于S的表达式

\[P=2\mu S+(-p+\lambda\nabla·\vec v)I\]

也即表面力对速度梯度的影响

雷诺输运定理

这个方程是下面两个方程(质量守恒+动量定律)的抽象化表述

设单位体积上有某一物理量$f(\vec x,t)$（可以是标量如ρ，也可以是矢量如ρv），此物理量的区域内积分为$I(t)=\iiint_Vf(\vec x,t)$

则区域积分I的变化率为区域积分的变化+流入的通量

\[\frac{D}{Dt}I(t)=\iiint_V \frac{\partial}{\partial t}f(\vec x,t)+\oint_{\partial V}f\vec v\cdot\vec{dS}\]

因为这看着足够有感觉了所以证明从略

质量守恒+动量定律

质量守恒：（密度的变化率=流入的密度通量）这种东西在物理里经常玩所以就懒得写具体推导了

\[\frac{\partial\rho}{\partial t}=-\nabla\cdot(\rho\vec v)\]

这个式子还可以继续改写，把右边的散度打开

\[\frac{\partial\rho}{\partial t}=-\rho\nabla\cdot \vec v-\vec v\cdot\nabla\rho\] \[\frac{\partial\rho}{\partial t}+\vec v\cdot\nabla\rho=-\rho\nabla\cdot\vec v\] \[\frac{D\rho}{Dt}=-\rho\nabla\cdot\vec v\]

动量定律：（动量的变化率=合力）

微控制体中动量的变化量来自于两个方面：1.内部动量变化2.动量流出

内部动量变化为

\[\frac{\partial(\rho \vec v)}{\partial t}\]

动量流出为(使用求和约定)

\[\frac{\partial}{\partial x^i}(\rho v^i\vec v)=(\rho \vec v\otimes\vec v)\vec \nabla=(v\cdot\nabla)\rho\vec v+\rho(\nabla·\vec v)\vec v\]

故总动量变化率为

\[\frac{\partial(\rho \vec v)}{\partial t}+(v\cdot\nabla)\rho\vec v+\rho(\nabla·\vec v)\vec v=\frac{D}{Dt}(\rho\vec v)+\rho(\nabla·\vec v)\vec v\\ =\frac{D\rho}{Dt}\vec v+\frac{D\vec v}{Dt}\rho+\rho(\nabla·\vec v)\vec v=\vec v(\frac{D\rho}{Dt}+\rho(\nabla·\vec v))+\frac{D\vec v}{Dt}\rho\]

由质量守恒，括号内的表达式为0，故总动量变化率可以化简为

\[\frac{D\vec v}{Dt}\rho\]

下面计算作用在微元上的质量力和表面力

质量力

\[\rho \vec F_b\]

表面力合力（力的梯度造成了力之差）$\vec p_i$表示在i面上所受力矢量,使用求和约定

\[\frac{\partial}{\partial x^i}\vec p^i\]

根据动量定理，有

\[\frac{D\vec v}{Dt}\rho=\rho \vec F_b+\frac{\partial}{\partial x^i}\vec p^i\]

注意到$\frac{\partial}{\partial x^i}\vec p^i$恰为应变张量P与矢量nabla的内积，故上式写作

\[\rho\frac{D\vec v}{Dt}=\rho \vec F_b+\vec\nabla·P\]

N-S方程

将

\[P=2\mu S+(-p+\lambda\nabla·\vec v)I\]

左右做散度

\[\vec\nabla·P=2\vec\nabla·(\mu S)-\nabla p+\nabla (\lambda\nabla·\vec v)\]

代入

\[\rho\frac{D\vec v}{Dt}=\rho \vec F_b+\vec\nabla·P\]

可得

\[\rho\frac{D\vec v}{Dt}=\rho \vec F_b+2\vec\nabla·(\mu S)-\nabla p+\nabla (\lambda\nabla·\vec v)\]

当流体的体积压缩膨胀效应较小时，将三方向法相压强平均值视作始终=静压强，此时可以通过这个等式消去第二粘度系数，仅留一个粘度系数μ

\[\lambda=-\frac{2\mu}{3}\] \[\rho\frac{D\vec v}{Dt}=\rho \vec F_b+2\vec\nabla·(\mu S)-\nabla p-\frac{2}{3}\nabla (\mu\nabla·\vec v)\]

上式被称为Navier-Stokes方程

更特殊地，在第一粘度系数处处相等的不可压流体中，有

\[\rho\frac{D\vec v}{Dt}=\rho \vec F_b+2\mu\vec\nabla·S-\nabla p\]

因为下面的计算要用，所以先将$\nabla·\vec v=0$这个式子打开

\[\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}+\frac{\partial w}{\partial z}=0\]

以第一个坐标x为例，两侧对x求偏导并移项，可得

\[\frac{\partial^2v}{\partial x\partial y}+\frac{\partial^2 w}{\partial x\partial z}=-\frac{\partial^2 u}{\partial x^2}~~(*)\]

计算$\vec\nabla·S$

\[\vec\nabla·S=\begin{pmatrix} \frac{\partial}{\partial x}&\frac{\partial}{\partial y}&\frac{\partial}{\partial z} \end{pmatrix} \begin{pmatrix} \frac{\partial u}{\partial x}&\frac{1}{2}(\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x})&\frac{1}{2}(\frac{\partial u}{\partial z}+\frac{\partial w}{\partial x})\\ \frac{1}{2}(\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x})&\frac{\partial v}{\partial y}&\frac{1}{2}(\frac{\partial v}{\partial z}+\frac{\partial w}{\partial y})\\ \frac{1}{2}(\frac{\partial u}{\partial z}+\frac{\partial w}{\partial x})&\frac{1}{2}(\frac{\partial v}{\partial z}+\frac{\partial w}{\partial y})&\frac{\partial w}{\partial z}\end{pmatrix}\]

以第一个坐标为例，

\[(\vec\nabla·S)_x=\frac{\partial^2 u}{\partial x^2}+\frac{1}{2}(\frac{\partial^2 u}{\partial y^2}+\frac{\partial^2 v}{\partial x\partial y})+\frac{1}{2}(\frac{\partial^2 w}{\partial x\partial z}+\frac{\partial^2 u}{\partial z^2})\]

将(*)式代入上式，可得

\[(\vec\nabla·S)_x=\frac{1}{2}(\frac{\partial^2 u}{\partial x^2}+\frac{\partial^2 u}{\partial y^2}+\frac{\partial^2 u}{\partial z^2})=\frac{1}{2}\nabla^2u\]

其他分量同理，故

\[\vec\nabla·S=\frac{1}{2}\nabla^2\vec v\]

代回特殊条件下的NS方程，可得

\[\rho\frac{D\vec v}{Dt}=\rho \vec F_b+\mu\nabla^2\vec v-\nabla p\]

进一步简化：无粘流体

\[\rho\frac{D\vec v}{Dt}=\rho \vec F_b-\nabla p\]

再进一步简化：静止流体

\[\rho \vec F_b=\nabla p\]

算是写完了，感受是：书上一笔带过的我硬写，书上详细证明的我懒得读