流体力学基础二:伯努利方程——对NS方程的简化
嗯,这里很符合我对物理的xp,物院没开流体太可惜了,我要自己写一遍
教材:周光坰《流体力学》
兰姆-葛罗米柯方程
书接上文NS方程,由动量定理可以推出
\[\rho\frac{D\vec v}{Dt}=\rho \vec F_b+\vec\nabla·P\]利用矢量恒等式(相当于是v的空间导数部分拆分为无旋部分和有旋部分)
\[(\vec v·\nabla)\vec v=\nabla\frac{v^2}{2}+(\nabla\times\vec v)\times\vec v\]代入得
\[\rho(\frac{\partial\vec v}{\partial t}+\nabla\frac{v^2}{2}+(\nabla\times\vec v)\times\vec v)=\rho \vec F_b+\vec\nabla·P\]这个就是兰姆-葛罗米柯方程
对无粘流体,P退化为静力压强标量-p
\[\rho(\frac{\partial\vec v}{\partial t}+\nabla\frac{v^2}{2}+(\nabla\times\vec v)\times\vec v)=\rho \vec F_b-\nabla p\]同除密度ρ
\[\boxed{\frac{\partial\vec v}{\partial t}+\nabla\frac{v^2}{2}+(\nabla\times\vec v)\times\vec v= \vec F_b-\frac{1}{\rho}\nabla p}\]本文下面两种简化全部基于此方程
第一种简化——伯努利积分
把前提放前面以免忘了:无粘+定常+体力保守+正压(密度只是压强的函数)
可选限制:重力场+不可压
定常:$\partial_t=0$
体力保守:$\vec F_b=-\nabla\pi$
处理一下$\frac{1}{\rho}\nabla p$,令
\[P=\int\frac{dp}{\rho(p)}\Rightarrow dP=\frac{dp}{\rho(p)}\Rightarrow\frac{1}{\rho}\nabla p=\nabla P\]综上,我们将带框的公式改写为
\[\nabla\frac{v^2}{2}+(\nabla\times\vec v)\times\vec v=-\nabla\pi-\nabla P\] \[\nabla(\frac{v^2}{2}+\pi+P)+(\nabla\times\vec v)\times\vec v=0\]现在沿着流线的方向积分,由于$(\nabla\times\vec v)\times\vec v$与v垂直,也即与流线方向垂直,所以积分时该项不作贡献,沿着流线有
\[d(\frac{v^2}{2}+\pi+P)=0\]也即,这个式子在同一条流线上守恒,我们用只与流线$\psi$相关的参数$c(\psi)$表示
\[\frac{v^2}{2}+\pi+P=c(\psi)\]这个式子已经可以用了,他描述了无粘定常流体(也就是说无摩擦,无能量损耗)同流线上拥有一致的机械能(但是NS是由动量定理导出的,也即是说得到这个式子的过程并没有直接用到能量守恒)
当密度为常数且势场为重力场时,令高度为y,则
\[\frac{v^2}{2}+gy+P=c_1(\psi)\]对于不可压流体,密度是常数,方程简化为
\[\frac{v^2}{2}+gy+\frac{p}{\rho}=c_1(\psi)\]上式即为不可压流体的伯努利积分(或定理)
点评:伯努利积分对有旋无旋均适用,因为沿流线积分恰好规避了旋度的问题;可以看出在同一条流线上,速度越大,压强越小,这很符合我们对伯努利的刻板印象对不对
伯努利积分的应用
虽然伯努利积分是对于单条流线而言,但是有些模型(细管)也可以近似看作同流线,应用是通过探测细管壁和细管中轴的压强差来计算流速关系
例:大桶水漏小孔

将模型视作定常,FRQ即为关注的流线,对于水面1点和出水口2点,由于压强都是大气压,由伯努利积分得
\[\frac{1}{2}v_1^2+gh=\frac{1}{2}v_2^2\]这不就自由落体吗,别装神秘了
由于水不可压,总通量为0
\[v_1A_1=v_2A_2\]且有
\[v_1=-\dot h>0\]三个未知数v1,v2,h,三个方程,可以化简出一个关于h的ODE
\[2gh=(\frac{A_1^2}{A_2^2}-1)\dot h^2\]理论上来说A1,A2是关于h的变量的话也可以照样解,但是这里只讨论A12均为常数的情况
\[\frac{dh}{dt}=-\sqrt{\frac{2gh}{\frac{A_1^2}{A_2^2}-1}}=-\sqrt{\frac{2g}{\frac{A_1^2}{A_2^2}-1}}\sqrt{h}\] \[\frac{dh}{\sqrt{h}}=-\sqrt{\frac{2g}{\frac{A_1^2}{A_2^2}-1}}dt\]两边定积分得
\[2\sqrt{h_0}=\sqrt{\frac{2g}{\frac{A_1^2}{A_2^2}-1}}\Delta t\]其中,Δt是流空所需总时间,解得
\[\Delta t=2\sqrt{\frac{\frac{A_1^2}{A_2^2}-1}{2g}h_0}\]还可以利用A1»A2进一步简化,$\frac{A_1^2}{A_2^2}-1\sim\frac{A_1^2}{A_2^2}$
\[\Delta t=\frac{A_1}{A_2}\sqrt{\frac{2h_0}{g}}\]点评:做了超多近似,真的还可以符合实际吗,担心
第二种简化——拉格朗日积分
核心使用前提:无旋+体力保守+正压
进阶前提:不可压+重力场+定常
伯努利要求的条件是定常,进而把对时间的偏导干掉;而在这里要求的是v无旋,进而把v旋度项干掉,还可以把时间导数项写作势梯度的形式,我们来看看如何操作
首先还是从这个开始
\[\frac{\partial\vec v}{\partial t}+\nabla\frac{v^2}{2}+(\nabla\times\vec v)\times\vec v= \vec F_b-\frac{1}{\rho}\nabla p\]无旋下,记$\vec v=\nabla\varphi$,且旋度项没有了,进而有
\[\nabla\frac{\partial\varphi}{\partial t}+\nabla\frac{v^2}{2}= \vec F_b-\frac{1}{\rho}\nabla p\]并且还是要求体力保守:$\vec F_b=-\nabla\pi$
和上面一样处理一下$\frac{1}{\rho}\nabla p$,令
\[P=\int\frac{dp}{\rho(p)}\Rightarrow dP=\frac{dp}{\rho(p)}\Rightarrow\frac{1}{\rho}\nabla p=\nabla P\]所以
\[\nabla\frac{\partial\varphi}{\partial t}+\nabla\frac{v^2}{2}= -\nabla\pi-\nabla P\] \[\nabla(\frac{\partial\varphi}{\partial t}+\frac{v^2}{2}+\pi+P)= 0\]也即被梯度项不依赖于空间,只依赖于时间,记作
\[\frac{\partial\varphi}{\partial t}+\frac{v^2}{2}+\pi+P=F(t)\]此式称为拉格朗日积分或柯西积分,在同一t下适用于全流场任何点
再附加上不可压+重力场+定常后可以进一步简化为
\[\frac{v^2}{2}+\frac{p}{\rho}+gy=F\]拉格朗日积分的运用
还就是内个大桶排水!
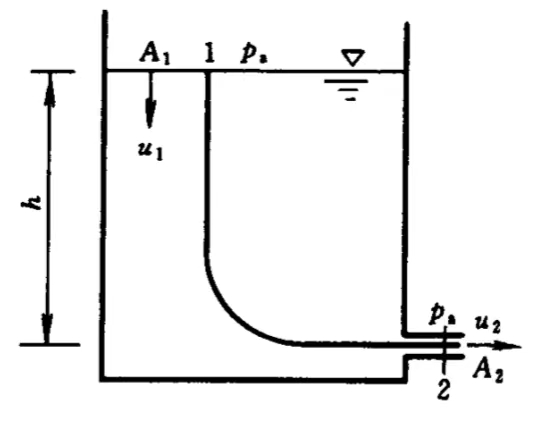
因为涉及到两个势能(重力势、速度势),所以先规定一下2处是重力势能0点,1处是速度势0点,于是有
\[\frac{v_1^2}{2}+\frac{p}{\rho}+gh=\frac{v_2^2}{2}+\frac{p}{\rho}+\frac{\partial\varphi}{\partial t}\]两边与大气相连且液体不可压,所以p项消掉,并且利用不可压代入$v_2=\frac{A_1}{A_2}v_1$得
\[\frac{1}{2}v_1^2[(\frac{A_1}{A_2})^2-1]-gh+\frac{\partial\varphi}{\partial t}=0\]计算速度势的时间导数,为了方便只积竖直部分
\[\frac{\partial \varphi}{\partial t}=\int_h^0\frac{dv_1}{dt}ds=-h\frac{dv_1}{dt}\]代入上面的方程可得
\[\frac{1}{2}v_1^2[(\frac{A_1}{A_2})^2-1]-gh-h\dot v_1=0~~~(*)\]理论上来说这已经给出了关于h的ode,但是他是非线性二阶的,不好解。为了给出一个近似解,现在暂时用到准定常(伯努利)给出的h-v1关系式
\[\frac{1}{2}v_1^2+gh=\frac{1}{2}v_2^2\Rightarrow v_1=\sqrt{\frac{2gh}{(\frac{A_1}{A_2})^2-1}}\]平方后两边对t求导
\[\dot v_1=\frac{g}{(\frac{A_1}{A_2})^2-1}\]代入*式后用h把v解出来
\[v_1=\frac{A_1}{A_2}\sqrt{2gh}\frac{1}{(\frac{A_1}{A_2})^2-1}\] \[v_2=\frac{A_1^2}{A_2^2}\sqrt{2gh}\frac{1}{(\frac{A_1}{A_2})^2-1}\]与伯努利导出的v1v2相比,这里的v1v2都近似增大了$\frac{1}{\sqrt{1-(\frac{A_2}{A_1})^2}}$倍,这个系数相当于考虑非定常时带来的一个修正量。
写完了,流体有点帅的啊
原创文章转载请注明出处: 流体力学二
