物批代数时间——李代数/李群的收缩扩张以及投影表示
令物批ドキドキする的代数时间袭来!
在本文中会给出1.庞加莱代数在c趋于无穷极限下收缩为伽利略代数。2.伽利略代数的某种非平庸中心扩张核对应着物理中的质量。3.李代数自由生成李群的投影表示对应着中心扩张李代数生成李群的表示。4.CFT2中的witt代数的中心扩张←这样一些fancy的结论
在代数品味方面,你可以看到一些关于扩张使用正合列与同调相联系的初级结果,以及中心扩张和射影表示之间正合列的平行关系。
前置:群论和一些qm,下面两个链接是我写的群论日记
https://zhuanlan.zhihu.com/p/684632353
https://zhuanlan.zhihu.com/p/692020167
本文主要抄A.Zee的群论(Group theory in a nutshell for physicists)第八章,和温伯格的量子场论第二章
前言-一些数学事实
关于李代数的微分算符形式
刘玉鑫的群论中有讲过,对于李群的函数空间表示,均可以通过无穷小展开将李群生成元与某个{对李群参数的偏导}相关的形式联系起来,也即导出李代数到微分算符形式的一对一关系,使得其在函数空间上的作用与李群表示同构,且保持李代数内部的加法和对易括号运算律(跟表示差不多的感觉了,只不过正儿八经的表示必须是一个线性变换)
至于怎么推导的因为偏离本文核心所以就不写了,直接把最常用的几个李代数的结论摆在下面
通用转动
\[J_{\mu\nu}=i(x_\mu\partial_\nu-x_\nu\partial_\mu)\]适用于绝大多数含转动的群(代数):SO(n)、SU(n)、伽利略代数、洛伦兹代数、庞加莱代数、高于二维的共形代数(反正目前我还没发现用不了的情况)
并且可以计算通用的转动生成元之间的对易关系
\[[J_{\mu\nu},J_{\rho\sigma}]=i(g_{\mu\rho}J_{\nu\sigma}+g_{\nu\sigma}J_{\mu\rho}-g_{\nu\rho}J_{\mu\sigma}-g_{\mu\sigma}J_{\nu\rho})\]其中g是度规
计算时用到了$\partial_ax_b=g_{ab}$
而在我们最熟悉的SO(3)中表现为
\[J_z=i(x\partial_y-y\partial_x)\] \[J_x=i(y\partial_z-z\partial_y)\] \[J_z=i(z\partial_x-x\partial_z)\]通用平移
\[P_\mu=-i\partial_\mu\]适用于大多数含平移的代数(反正目前我还没发现用不了的情况)
半直积
在接触庞加莱群时,难免会碰到$\rtimes$,所以第一次接触还是要有个正确的印象
内半直积:令G为群,N为G的正规子群,H是G的子群;若G=NH且$N\cap H={e}$,则称G是N和H的内半直积,或G在N上分裂,写作$G=N\rtimes H$
注:这个条件有很多等价形式,大意就是依据N的正规性推出这个N可以无交划分原群G的这种感觉。然后就是半直积的开口方向朝正规子群方向
这玩意还蛮普遍的,基本上你随便搞一个正规子群,大多数情况下都有这种无交划分,那就是内半直积了
但是呢内半直积的建立必须得有一个大群G罩着,能不能像别的构造方式(直积、张量积)一样,直接把没啥关系的两个群牵起来呢?答案是可以的,但是你得先找到一个符合条件的群同态,看下面外半直积
外半直积:对于任意两个群H与N,以及一个群同态$\varphi:H\to Aut(N)$,即可定义一个这样的新群$N\rtimes_\varphi H$,称作N和H相对于φ的外半直积
其元素形式继承集合直积$N\times H$,而群运算*定义为
\[(n_1,h_1)*(n_2,h_2)=(n_1\varphi(h_1)(n_2),h_1h_2)\]可以验证这确实是个群
还是先看下方向,φ由半直积符号的闭口方向引出开口方向的一个自同构
外半直积是一个比内半直积、直积更广的一种构造形式,它可以轻松退化到内半直积和直积
外半直积退化到内半直积:以外半直积$N\rtimes_\varphi H$为大群,则$N\times{e_H}$与${e_N}\times H$的内半直积就是这个外半直积
外半直积退化到直积:直接令φ是平庸群同态
内半直积也可以用外半直积的语言描述。假如我有了$G=N\rtimes H$,那么令$\varphi:H\to Aut(N);\varphi(h)(n)=hnh^{-1}$是伴随作用,(由于N的正规性可以看出他确实是个Aut),那么G同构于$N\rtimes_\varphi H$
那么至于我们的庞加莱群,被定义为
\[R^{1,3}\rtimes SO(1,3)\]先从外半直积的角度思考,SO(1,3)确实可以通过伴随作用打到Aut(R^{1,3})上,毕竟旋转一下-平移-再转回来,这还在平移里面没问题
他的特殊性就是φ恰好是个伴随变化,所以子群R^{1,3}在大群里正规了,并且和SO(1,3)不交,那么用内半直积也没问题
至于维度方面,很明显半直积的大小等于两个小群大小的乘积
链复形与正合列
一个链复形
\[...\to M_{i-1}\xrightarrow{f_i}M_i\xrightarrow{f_{i+1}}M_{i+1}\to...\]要求$f_{i+1}\circ f_i=0$,也即$imf_i\subset kerf_{i+1}$
定义$B_i=imf_i,Z_i=kerf_i$,则上同调群定义为$H_i=Z_{i+1}/B_i$,衡量了与正合列(见下文)的差别
正合列
\[0\to M'\xrightarrow{f}M\xrightarrow{g}M''\to0\]要求$kerg=imf\Rightarrow M’‘\simeq M/M’$,且上同调群H平凡
李代数收缩
大名叫Inönü-Wigner收缩;实际上就是让李代数某个参数取极限(∞或0),这样让它在极限情况下成为另一个李代数
so(3)收缩到E(2)的代数
在so(3)中,进行换元,令$z=Lw$,其中L是参数,w用来替代z成为新的坐标;并取极限$L\to\infty$,此时$\partial_z=\frac{1}{L}\partial_w\to 0$
\[J_z=i(x\partial_y-y\partial_x)\] \[J_x=i(y\partial_z-z\partial_y)\to-i(Lw)\partial_y=LwP_y\] \[J_y=i(z\partial_x-x\partial_z)\to i(Lw)\partial_x=-LwP_x\]意思就是把z轴无限放大,其实跟换元倒是关系不大
那么对易关系变为
\[[J_x,J_y]=iJ_z\Rightarrow[P_y,P_x]=-J_z/(Lw)^2\to0\]↑代入了上面的极限情况下生成元
\[[J_z.J_x]=iJ_y\Rightarrow[J_z,P_y]=-iP_x\] \[[J_z,J_y]=-iJ_x\Rightarrow[J_z,P_x]=iP_y\]得到的新对易关系恰好是二维欧几里得代数(二维平面上的旋转平移)的对易关系;也就是说我们通过取极限并重新规定生成元构造出了一组新的李代数,他正是E(2)对应的李代数
直观上理解就是把z拉到无限长,然后z方向基矢就会缩到很短(?其实这个很迷),z轴刻度变得密集(只有刻度密集才会有平移近似),那么绕x或y的转动就会近似为沿y或x的平移,画了个图便于直观感受
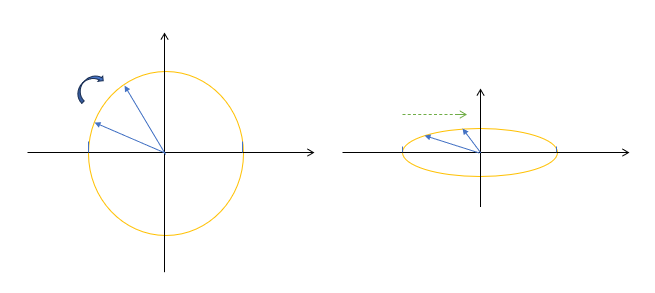
洛伦兹代数收缩到ISO(3)所对应的代数
前言:不妨先看看生成元个数,洛伦兹是3个推动3个转动,ISO(3)是3个平移3个转动,正好推动收缩到平移上
我们都知道狭相坐标变换的低速近似就是伽利略变换;庞加莱群描述了狭相下的4个时空平移和3个推动3个转动,共10维;而伽利略群描述了(1)3个维度的空间旋转(2)3个维度的空间平移(3)时间与空间的平移(4)一个维度的时间演化,共十维;通过取极限v«c,也就是令$c\to\infty$,可以让庞加莱群还原到伽利略群
但是在这里以转动部分为例,演示子群洛伦兹群对应的代数收缩到iso(3)
取$x^0=ct$,以及(-+++)的闵氏度规,则
\[J_{0i}=i(-ct\partial_i-x^i\frac{1}{c}\partial_t)=-ict\partial_i=ctP_i\]而空间转动$J_{ij};i,j\in{1,2,3}$不与c相关,所以取极限不改变,下面看看对易关系如何变化
\[[J_{0i},J_{0j}]=-iJ_{ij}\Rightarrow[P_i,P_j]=-\frac{i}{(ct)^2}J_{ij}\to 0\] \[[J_{0i},J_{kl}]=i(\delta_{il}J_{0k}-\delta_{ik}J_{0l})\Rightarrow[P_i,J_{kl}]=i(\delta_{il}P_k-\delta_{ik}P_l)\Rightarrow[P_i,J_j]=i\varepsilon_{ijk}P_k\]这正好满足伽利略代数的子代数iso(3)的运算规律,可见在低速近似下我们确实将洛伦兹群的3个boost收缩为3个空间平移,不错
庞加莱群和伽利略群比上面两个多出来的东西分别是{时空平移部分}和{时间与空间共同平移和时间演化},但是伽利略群的时间与空间没有关联,故在做时间与空间共同平移时,实际上只平移了某个方向的空间,而时间保持“绝对性”,所以这多出来的两坨就是两坨4维平移,可以看出是同构的,我就不具体写了
李代数中心扩张
单李代数:自身非abel且无非平庸理想
半单李代数:自身非abel且无非平庸的abel理想(比单李代数可以多非abel理想)
半单李代数一定可以写作有限个单李代数的直和
群的扩张都是由一个正合列描述
\[1\to N\xrightarrow i G\xrightarrow pQ\to 1\](提醒你一下$G/N\simeq Q$)称群G为Q(对N)的扩张;当N落在G的中心时被称为中心扩张
那么到李代数这边,还是有三个李代数a e g,满足正合列
\[0\to a\to e\to g\to 0\]且有a在e的中心,即$[a,e]=0$(在不可约表示中由舒尔引理可知a正比于单位线性算符),e为g的中心扩张
物批会干的事情就是在李代数对易关系中塞一个“常数”,被称作中心荷(central charge)
李代数的上同调群被定义为$H^n(g,M):=Ext^n_{U_g}(R,M)$,其中M是g的一个表示
李群李代数的投影表示
这里实际上有三件事(或者六件事):投影表示和扩张的关系、投影表示和上同调的关系、扩张和上同调的关系。(出处见参考1)
在qm中,两个态之间相差常数c仍然是同一个态,但是又要求所有态归一,也即态模长一样;所以能差的就只有一个模长为1的复数——(全局)相位
体现到李群上,允许这样相差相位的(准)表示U
\[U(T)U(T')=e^{i\phi(T,T')}U(TT')\]体现在李代数上,允许这样的ρ
\[[\rho(x),\rho(y)]=\rho([x,y])+c(x,y)·id\]域F上线性空间V的射影线性变换群被定义为
\[PGL(V)=GL(V)/F^*\]其中,$F^*$是由所有非零倍数的恒等变换组成的正规子群
下面在复数域上讨论李代数的表示,将线性变换群李代数化,则射影线性变换群可写入如下正合列
\[0\to C^*\to gl(V)\xrightarrow{\pi_2}pgl(V)\to 0\]为了给李代数g找一个投影表示,我们尝试先把李代数g打到另一个中介李代数$\tilde{g}$上,给这个$\tilde{g}$找一般表示,该表示诱导出g的投影表示,画交换图就是这样的
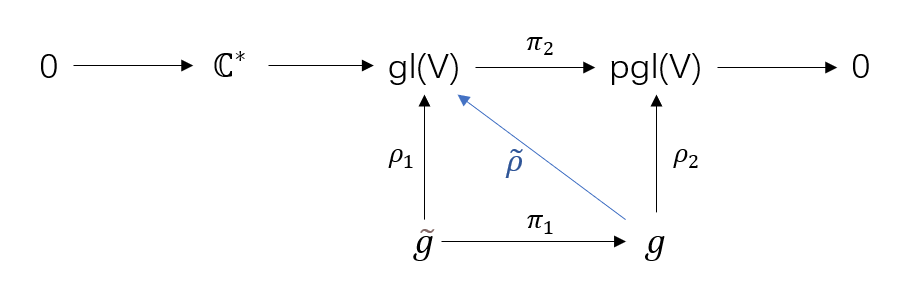
其中,ρ1是一个真正的表示,$\tilde{\rho}$是我们要找的投影表示,$\tilde{\rho}$模掉C*就是ρ2,后者像空间在pglV上,但是仍然是g的一个同态
这时候你看看李代数对某个数域的中心扩张,是不是刚好和第一排平行的的,我们把它补上
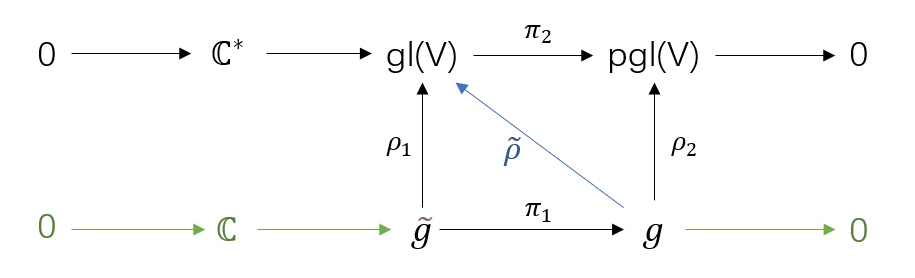
发现当$\tilde{g}$是g的对C的中心扩张时,是可以满足上面的交换图的,进而可以由$\tilde{g}$的表示给出g的投影表示
在下面可以看到函数形式上投影表示和中心扩张的关系
对于一个李代数投影表示$\tilde{\rho}$,有
\[[\tilde{\rho}(x),\tilde{\rho}(y)]=\tilde{\rho}([x,y])+c(x,y)·id~~~(*)\]其中,c(x,y)将李代数中的元素映射到复数域上,继承了李代数的(1)双线性(2)反对称(3)雅可比(就是你每个李代数恒等式都可以导出关于c的恒等式);并且每个投影表示与函数c(x,y)一一对应,把这样的函数c全部放到一起,发现在加法下封闭,记作$c(x,y)\in Z^2(g,C)$,称为2-闭上链(2-cycle)
这个Z看起来是不是和上同调群有点关系?是的,下面会和李代数的二阶上同调群联系起来
但是有一类相位差,总是可以通过平移重定义生成元的方式消去,他们是平庸的;比如说相差全局相位的两个表示
\[\tilde{\rho}'(x)=\tilde{\rho}(x)+a(x)·id\]这就是纯属生成元的平移,我们不加证明的说这两个投影表示等价(其实等价应该是一个交换图给出的定义),代入投影表示的定义(*)式,可得$\tilde{\rho}’$所对应的相位附加函数与c(x,y)的关系
\[c'(x,y)=c(x,y)-a([x,y])\]将a[·,·]看作李代数上的二元函数,使用c(x,y)所满足的性质,可得a[·,·]也满足这三条;也即a[·,·]构成了阿贝尔群$Z^2(g,C)$的正规子群,记作$B^2(g,C)$
在温伯格场论中反着推的,告诉你函数长什么样就一定是平庸的相位
那么我们当然关注的是投影表示的等价类了,所以自然要把这些平凡的相位差模掉,故投影表示的等价类由${H^2}’(g,C)=Z^2(g,C)/B^2(g,C)$描述(这东西据说就是李代数的2阶上同调群,但是我不会证)
李代数的中心扩张
g对C中心扩张后元素(未定义运算)可以由$C\oplus g$来描述,设映射$\sigma_1:g\to\tilde{g}$,满足$\pi_1\circ\sigma_1=id_g$
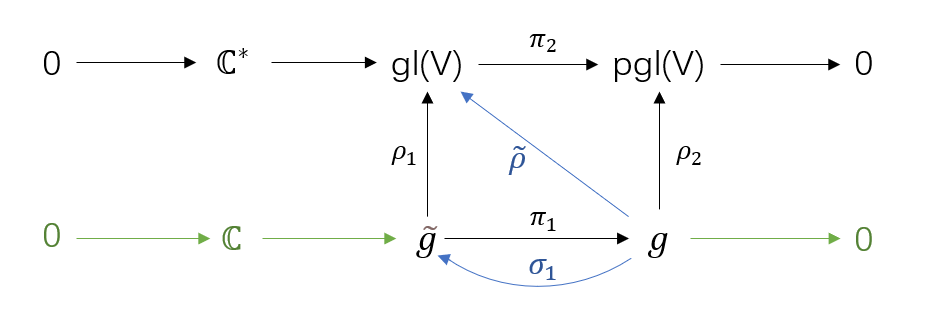
pi是自然同态,意思就是把C模掉;那么这个σ就有一个附加自由度,把g打到$\tilde{g}$的时候保持g部分不变就好,可以随意加一些常数项,也是满足$\sigma_i:g\to\tilde{g}$,满足$\pi_1\circ\sigma_i=id_g$的。
群扩张可以由σ,以及相差的常数函数来描述
\[[\sigma_1(x),\sigma_1(y)]=\sigma_1([x,y])+\varepsilon(x,y)\]还有一种脱离σ定义的运算关系
\[[a\oplus g_1,b\oplus g_2]=[g_1,g_2]+\varepsilon(g_1,g_2)\]其中,函数ε将李代数上的两个元素映射到C上。然后你代李代数的三个运算性质,会发现这个ε和上面的c定义完全一样,ε也在$Z^2(g,C)$内
剩下的对平庸中心扩张(等价于g与C两个代数的直和)的讨论和上面的投影表示一样了,最后还是能得出结论,g对C的非平庸中心扩张等价类为${H^2}’(g,C)=Z^2(g,C)/B^2(g,C)$
然后就是wiki上还是能查到这个结论(见文末参考2),但是我不会证明

李代数到李群投影表示结论(Weinberg第一卷P61):若李代数所有中心扩张平庸,则其对应的单连通李群没有非平庸投影表示。
证明书上也有,用无穷小展开取路径证的
李代数的二阶上同调群的性质(文末参考3):半单有限维李代数的二阶上同调群平庸,故这些李代数只有平庸的中心扩张
这个证明书上没有,我也不会证
结合上面两个定理可以得出推论:半单有限维李代数(及对应的连通李群)的投影表示平庸
Bargmann定理(见参考5):单连通有限李群G的二阶上同调群平凡
\[H^2(G,R)=0\]书上有证明,用到了普通线性空间到射影线性空间的映射与标量变化空间纤维丛的关系,然后证明任意的投影表示平凡
伽利略代数的中心扩张
伽利略代数包含3个平移生成元P,3个空间转动生成元J,3个匀速换系(平移)生成元K,一个时间平移生成元H,其对易关系写作
\[[J_i,J_j]=i\varepsilon_{ijk}J_k~~~~~[J_i,P_j]=i\varepsilon_{ijk}P_k~~~~~[J_i,K_j]=i\varepsilon_{ijk}K_k\]由空间矢量生成元J的对易关系(参考4),可以先写出J关于PJK的对易关系
\[[P_i,H]=0~~~~~[J_i,H]=0~~~~~[K_i,H]=iP_i~~~~~\]动量和角动量与H对易,但是匀速换系生成元K不能保持能量守恒,和H不对易(会附加上某个轴的动量)
\[[P_i,P_j]=0~~~~~[K_i,P_j]=0~~~~~[K_i,K_j]=0~~~~~\]剩下三个都是对易的
可以看出由平移生成元(动量)构成的子空间是伽利略代数的非平凡abel理想,所以伽利略代数不是半单的
对他进行扩张也即在每个对易关系后加一个函数c(x,y),满足2-cycle条件,这种非平庸的扩张可能是不唯一的,但是我们只取一种,即
\[c(K_i,P_j)=iM\delta_{ij}\]而在其他生成元上取值均为0;其中M是常数
为了看出这个常数的物理意义确实是质量,我们来算几个有能量物理意义的对易关系,比如说匀速换系和动能的关系
\[[K_i,\frac{P^2}{2M}]=\frac{1}{2M}(P_j[K_i,P_j]+[K_i,P_j]P_j)=\frac{1}{2M}(2iM\delta_{ij}P_j)=iP_i\]且有$[K_i,H]=iP_i$,故$[K_i,H-\frac{P^2}{2M}]=0$;然后你可以验证$H-\frac{P^2}{2M}$与剩下7个生成元均对易(与H显然,与P也是两个0,与J因为[J,P^2]=0所以也是0了),那么在某个不可约表示中$H-\frac{P^2}{2M}$就是个单位算符的常数倍,为了符合物理品味记这个算符为V
\[H=\frac{P^2}{2M}+V\]再联系先前就给出的李代数在函数空间上的算符表示,$H=i\frac{\partial}{\partial t},P=-i\frac{\partial}{\partial x^i}$,将这个等式作用在函数$\psi$上,可得
\[i\frac{\partial}{\partial t}\psi=-\frac{1}{2M}\nabla^2\psi+V\psi\]这正是$\hbar=1$下的薛定谔方程,所以可以看出中心荷M的物理意义确实是质量
DLC:伽利略代数的相对论化
在经典时空观中,坐标系匀速变换时间保持不变,但是狭义相对论中换系时间与空间必须同时变化;受到这个启发,我们在伽利略匀速换系生成元中添加时间项
\[K_i=-it\frac{\partial}{\partial x^i}\to k_i'=-i(t\frac{\partial}{\partial x^i}+x\frac{\partial}{\partial t})\]最后令c->∞,回到经典,$\partial_t=-iH=-iM$,可以发现这样的修改定义和上面的中心扩张添加M是等价的
Witt代数的中心扩张
Witt代数来自于2维共形代数$\mathfrak{cft}_2$的一半,是一个无穷维的李代数(在全局下退化为三个生成元,其同构于su(2)),其对易关系如下
\[[L_m,L_n]=(m-n)L_{m+n}~~~;m,n\in Z\]现在对他进行一个扩张,设扩张的函数为p(x,y)配上一个常系数c,即
\[[L_m,L_n]=(m-n)L_{m+n}+cp(L_m,L_n)\]然后由于p这个函数的双边线性性,无论自变量取怎样的线性组合,都可以把他拆分成自变量只有生成元Ln的形式,所以我们下面就不在p(,)里面塞(生成元以外的)常数了,简记为$p(L_m,L_n)=p(m,n)$,右侧的m和n拥有生成元标号的意义,此时
\[[L_m,L_n]=(m-n)L_{m+n}+cp(m,n)\]反对称条件
\[p(m,n)=-p(n,m)~~(1)\]雅可比恒等式条件
\[(n-k)p(m,n+k)+(k-m)p(n,k+m)+(m-n)p(k,m+n)=0~~(2)\]接下来看看平庸扩张a([x,y])所满足的等式
\[a([m,n])=(m-n)a(m+n)~~(3)\]在2中令k=0,得
\[np(m,n)-mp(n,m)+(m-n)p(0,m+n)=0\]使用反对称条件(1),有
\[(n+m)p(m,n)+(m-n)p(0,m+n)=0\]也即,当$m\neq -n$时,p(m,n)只与m+n有关。下面试图找到p(0,m+n)的关系,注意到平庸扩张a也可以视作单变量的,所以想着利用一下这个条件,在(3)式中取m=0,有
\[a([0,n])=-na(n)\]并且一个任意的a如果在第一个变量为0时满足上式即为一个平庸扩张,而na(n)是一个任意的形式。我们可以在待求的扩张中任意添加平庸扩张的倍数,其扩张都是互相等价的,不妨直接令这些第一个变量为0的输入都输出0,即规定
\[p(0,n)=0,\forall n\in Z\Rightarrow m\neq -n,p(m,n)=0\]这个过程类似于你取磁矢势A,但是他可以添加任意的梯度,然后库伦规范就规定A的散度为0,都是一种为了方便的人为规定
接下来只需要研究m=-n项$p(n,-n)$,这大大简化了计算范围,直接将p(n,-n)记作p(n),在(2)中令k=m+n,有
\[(1-2n)p(1)+(2-n)p(n)+(n+1)p(n-1)=0\]再利用(3)条件,取a([1,-1])
\[a([-1,1])=2a(0)\]还是像之前一样,我们可以同时规定c(-1,1)=0
这样就有了p(n)的递推式
\[p(n)=\frac{n+1}{n-2}p(n-1)\]连乘就好,故
\[p(n)=\frac{(n+1)n(n-1)}{6}p(2)\]把待定系数c与p(2)乘在一起,可以只写一个待定系数c,然后跟着大家习惯,再除个2也没问题,得到扩张之后的代数
\[[L_m,L_n]=(m-n)L_{m+n}+\frac{c}{12}(m^3-m)\delta_{m+n,0}\]这个就是Virasoro代数
已完结
参考
0.A.Zee的群论(Group theory in a nutshell for physicists)第八章,和温伯格的量子场论第二章
1.https://www.zhihu.com/question/517500343
2.https://en.wikipedia.org/wiki/Lie_algebra_cohomology
3.Blumenhagen,《Introduction to Conformal Field Theory》P16
4.喀兴林《高等量子力学》
5.Schotten,《A Mathmatical Introduction to Conformal》
原创文章转载请注明出处: 李代数投影表示与中心扩张
