【同步更新】物理向群论2:随手记
从这里开始我会边补量力(代数部分)边学群论,所以会有很多初学量力的证明、引理等记号;以下大部分矩阵(算符)未经声明均为厄米矩阵、未经声明均在C上研究
不要以为群论就全在C上了,su(2)代数配备的数域是R
阅读提示:本文大多数带有注释块(底色略暗?)的文字是本人出于xp与数学上的完整性而给出的数学证明,不合你xp的话可以只看下命题不看证明
完蛋,拍封面的时候发现波奇的呆毛早就不知道掉哪里去了
上篇:https://zhuanlan.zhihu.com/p/684632353
\[\require{physics}\]代数与量力补充
定义:厄米矩阵:共轭转置等于自身
幺正矩阵(酉阵):共轭转置等于自身的逆
引理0.1:n阶厄米矩阵A拥有n个实特征值
证:特征值共有n个,由代数基本定理易得
任取一特征值$a+bi(a,b\in R)$及特征向量$\ket{x}$,利用$A^\dagger=A$则有
\[<x|Ax>=<x|(a+bi)x>=(a+bi)<x|x>=<Ax|x>=(a-bi)<x|x>\]由于$\braket{x}{x}x\in R_{>}$,故$a+bi=a-bi,b=0$特征值为实数
引理0.2:厄米矩阵特征值代数重数=几何重数
证明:任取一特征值λ,令B=A-λI,原命题等价为$\forall k\in Z_{>},ker(B^k)$为常空间
对任意矩阵均有核空间上升链
\[ker(B)\subset ker(B^2)\subset ker(B^3)\subset ...\]而对厄米矩阵B,取$x\in ker(B^2)$,则有$B^2x=0\Rightarrow B^TBx=0\Rightarrow x^TB^TBx=0$ $\Rightarrow<Bx,Bx>=0\Rightarrow Bx=0$
以此类推,结合核空间上升链,可得
\[ker(B)=ker(B^2)=ker(B^4)=...=ker(B^{2^n})\]由此以及核空间上升链夹逼可得$\forall k\in Z_{>},ker(B^k)$为常空间,证毕
提示:引理0.1和0.2告诉了我们厄米矩阵特征向量的完备性
引理0.3:厄米矩阵A不同特征所对应的特征向量正交
证明:设A有特征值m,对应特征向量$\ket{x}$,以及特征值n,对应特征向量$\ket{y}$且$n\neq m$,则
\[<x|A|y>=n<x|y>=<Ax|y>=m<x|y>\]由于$n\ne m$,故只能$\braket{x}{y}=0$,特征向量正交
在同一特征值下若存在大于1维的特征空间,则可以通过正交化找出其中一组正交基
综上,厄米矩阵的特征向量张成了一组正交归一完备基
引理0.4:由厄米矩阵A构成的二次型,其值必定是实数
任取$\ket{x}$,则由厄米阵特征向量的完备性,可以将$\ket{x}$在基$\ket{i}$下展开,写作$\ket{x}=\sum_i\ketbra{i}\ket{x}$;设$\ket{i}$在A下的特征值是i,则关于x的二次型
\[<x|A|x>=\sum_{i,j}\overline{<j|x>}<j|A|i><i|x>\]由|i>的正交性
\[<x|A|x>=\sum_{i}\overline{<x|i>}<i|A|i><i|x>=\sum_i i\overline{<i|x>}<i|x>\]后者求和内全为实数,故总和为实数
注:这个二次型除掉向量x的模方后得到的就是算符的期望值
引理0.5:由幺正变换U联系的两个相似厄米矩阵,具有全同的谱,只是特征向量之间差了变换U
证明:设A是厄米阵,A|i>=i|i>,则
\[UAU^{-1}U|i>=iU|i>\]总结:对易算符的特征矢全同,但谱不一定全同;由幺正变换联系的相似算符特征矢不一定全同,但谱一定全同。
引理0.6:(Brocker etal.(1985)P165)紧致的连通李群的指数映射是满射,这等价于任一群元都属于某一单参子群
证明:如果用到了再证
引理0.7:对于方阵A,有
\[|e^A|=e^{tr(A)}\]证明:利用所有矩阵均可上三角化的特性
令$A=PDP^{-1}$,其中D是上三角方阵,$tr(A)=tr(D)$=对角线元素和
观察上三角矩阵的幂次中,其对角矩阵始终独立地进行同步幂次提升,也即
\[(D^n)_{ii}=(D_{ii})^n\]并且上三角的幂次仍然是上三角,故
\[e^D_{ii}=1+D_{ii}+\frac{D^2_{ii}}{2!}+\frac{D^3_{ii}}{3!}+...=e^{D_{ii}}\] \[|e^A|=|Pe^DP^{-1}|=|e^D|=\Pi e^{D_{ii}}=e^{\sum D_{ii}}=e^{tr(A)}\]他的意义:李群要求det=1对应了李代数的无迹
物理知识补充:
下文的生成元J在忽略系数时即为角动量算符,J^2是总角动量算符,J3是任意轴角动量算符
量子数(类似于sinkx,物理量离散化时用于计数的变量)
n=nr+nφ,总量子数
s:(总)自旋角动量模长,单电子总为1/2
$m_s$:自旋角动量,正负表示方向
l:轨道角动量=nφ-1
j:总角动量模长(单电子系统j=s)
m:总角动量在某一方向(轨道方向)上的投影量子数
物理定理0.1(基本对易关系):在理论力学中,我们有传统泊松括号上的$[p_i,p_j]=0;[q_i,q_j]=0;[q_i,p_j]=\delta_{ij}$,而在量子力学中,这个对易关系被推广到
\[[x_i,x_j]=0;[p_i,p_j]=0,[x_i,p_j]=i\hbar \delta_{ij}\]若用$\hat p=-i\hbar\frac{\partial}{\partial x}$代入验证上式,则只需要用到乘积求导法则,是很简单的
物理公式0.2(幂次李括号):
\[[a,b^n]=\sum_{i=0}^{n-1}b^i[a,b]b^{n-1-i}\]证明:
\[\begin{aligned} [a,b^n] & = ab^n-b^na \\ & = ab·b^{n-1}-ba·b^{n-1}+ba·b^{n-1}-b^na \\ & = [a,b]b^{n-1}+ba·b^{n-1}-b^na \\ & = [a,b]b^{n-1}+b[a,b]b^{n-2}+b^2ab^{n-2}-b^na \\ & = ... \\ & = \sum_{i=0}^{n-1}b^i[a,b]b^{n-1-i} \end{aligned}\]
物理定理0.3(经典与量子括号的衔接,sakurai P47):
在经典泊松括号下
\[[x,F(p_x)]=\frac{\partial F(p_x)}{\partial p_x},~~~~[p_x,F(x)]=-\frac{\partial F(x)}{\partial x}\]在qm框架下,对可以幂级数展开的函数$F(\vec x)$与$G(\vec p)$,有如下的的对易关系
\[[x_l,G(\vec p)]=i\hbar\frac{\partial G}{\partial p_l},~~~~[p_i,F(\vec x)]=-i\hbar\frac{\partial F}{\partial x_i}\]证明:只证量子部分(理力忘了就去看我写的note(x))
设$G(\vec p)=\sum_{i,j,k} g_{i,j,k}p_1^ip_2^jp_3^k,g_{i,j,k}\in\mathbb{C}$(多元函数展开),则
\[[x_l,G(\vec p)]=\sum_{i,j,k} g_{i,j,k}[x_l,p_1^ip_2^jp_3^k]\]代入基本对易关系$[p_i,p_j]=0,[x_i,p_j]=0(i\ne j)$后有
\[[x_l,p_1^ip_2^jp_3^k]=p_a^ip_b^j[x_l,p_l^k]\]其中,$p_a,p_b$是非l方向上动量算符;ijk是轮换对称求和哑变量,所以总可以进行一次重排序;由上一定理(0.2)以及基本对易关系$[x_i,p_i]=i\hbar$可得
\[[x_l,p_l^k]=\sum_{i=0}^{k-1}p_l^i[x_l,p_l]p_l^{k-1-i}=i\hbar kp_l^{k-1}=i\hbar\frac{\partial}{\partial p_l}p_l^k\]代回到原式中
\[[x_l,G(\vec p)]=i\hbar\sum_{i,j,k} g_{i,j,k}p_a^ip_b^j\frac{\partial}{\partial p_l}p_l^k=i\hbar\frac{\partial G}{\partial p_l}\]第二个关于F(x)的式子同理可得
特例撒谎代数与群
承接上篇:物理向群论1
so(3)的不可约表示
引理1.1:设在线性空间V下有厄米矩阵A、B,则AB可交换<=>A、B拥有同一套特征向量
证明:先证充分性,若A的特征值代数重数均为1,
取A的特征值为n下的特征向量x,则有
\[ABx=BAx=nBx\]也即,$Bx$与x共线,故x也是B的特征向量;由于x选取的任意性且A与B特征数相同,所以A和B共用同一套特征向量
若A存在代数重数大于1的特征值(有简并)
首先先将A中无简并的特征向量所张成的空间记作W,可以证明这些特征向量也是B的特征向量,故仅需考虑V-W,也即出现简并的特征向量是否仍有空间到空间的对应关系
设V-W由B的特征向量${y_1,…,y_l}$张成,对应的特征值为${b_1,…,b_l}$
不妨设A拥有重数为c的特征值,同上证明易得V-W内含有一个c维的B作用下的不变子空间M;欲证这个不变子空间恰好可以由B的一组特征向量张成,所以反证:假设${y_1,…,y_l}$落在$M$上的数目$< dim M$,又因为{y}的完备性,总可以造出$y’\in M,y’=\sum_{i}c_iy_i$,使得求和号中的yi均不在M上,且这些yi所对应的特征值不全相同(否则,y’也是B的特征向量)
下面考虑B作用在y’上,由于b_i不全相同,所以$\exists k,t\in \mathbb C,t\neq 0$有分解
\[By'=\sum_i c_ib_iy_i=k\sum_i c_iy_i+ty'',y'=\sum_i c_iy_i\in M,y''\in V-M\]这与不变子空间的条件相矛盾,故A的每个特征空间上均存在B特征向量构成的基,也即A、B拥有同一套特征向量
再证必要性
设A、B拥有同一套特征向量$\ket{i}$,分别对应特征值$a_i,b_i$,则任取非零向量$\ket{x}$,有
\[[A,B]|x>=\sum_i[A,B]|i><i|x>=\sum_i(a_ib_i-b_ia_i)|i><i|x>=0\]由于向量|x>的任意性,可得[A,B]=0,也即A、B可交换
上述定理的物理意义:算符A、B对易<=>A、B拥有完备的共同本征态<=>A、B可以被同时测量,可以同时拥有测量值
对于不对易的算符,只可以在其共同本征态张成的子空间内同时被测量(例如当$J^2=0$时,$J_x=J_z=0$)
推广:用线性函数联系的两个厄米算符可以同时对角化
在本节中,考虑三元李代数{$J_1,J_2,J_3$},拥有运算律$[J_k,J_l]=i\varepsilon_{klm}J^m$,我们尝试从找到特征向量的方式给出以特征向量为基的厄米矩阵表示
注:$J^2,J_{\pm}$这些辅助算符及对易关系已在上一篇写出、包括上升下降算符的截断与对模长的改变,这里不再赘述。注意到$J^2$与$J_3$对易,故他们拥有共同的一组特征向量;设某个特征矢量,在$J^2$下拥有特征λ,在$J_3$下拥有特征m,则总可以通过上升下降算符和截断造出一组2j+1个特征基
\[\{|j,m>|m=0,\pm1,...,\pm j\}\]其中,相对$J^2$的特征值为j(j+1),相对$J_3$的特征值为m
再者,已知$J^2,J_\pm$在这一组基上的作用效果,也即表示矩阵已知
实例:so(3)的二维表示(j=1/2):此时m可取$\pm\frac{1}{2}$,也即有特征基$\ket{\frac{1}{2},\frac{1}{2}},\ket{\frac{1}{2},-\frac{1}{2}}$,将$J^2,J_\pm$作用于此
\[J^2|\frac{1}{2},\pm\frac{1}{2}>=\frac{3}{4}|\frac{1}{2},\pm\frac{1}{2}>\] \[J_+|\frac{1}{2},\frac{1}{2}>=0,J_+|\frac{1}{2},-\frac{1}{2}>=|\frac{1}{2},\frac{1}{2}>\] \[J_-|\frac{1}{2},\frac{1}{2}>=|\frac{1}{2},-\frac{1}{2}>,J_-|\frac{1}{2},-\frac{1}{2}>=0\]由此可以写出矩阵形式
\[J^2 =\begin{pmatrix} \frac{3}{4}&\\ &\frac{3}{4} \end{pmatrix};J_+ =\begin{pmatrix} &1\\ & \end{pmatrix};J_- =\begin{pmatrix} &\\ 1& \end{pmatrix}\]还原到J123
\[J_1 =\frac{1}{2}\begin{pmatrix} &1\\ 1& \end{pmatrix};J_2 =\frac{1}{2}\begin{pmatrix} &-i\\ i& \end{pmatrix};J_3 =\frac{1}{2}\begin{pmatrix} 1&\\ &-1 \end{pmatrix}\]用泡利矩阵写出,也即
\[J_k=\frac{\sigma_k}{2}\]以上是so(3)的2维表示,下面试图通过这个表示去寻找SO(3)的表示
SO(3)的不可约表示
利用固定轴的欧拉角参数化SO(3),有一个好处就是两端绕3轴旋转恰在基矢下退化为特征值(标量),直接计算U作用在基上后再在基上的展开系数:
\[U(\alpha,\beta,\gamma)=e^{-i\alpha J_3}e^{-i\beta J_2}e^{-i\gamma J_3}\] \[<jm'|U|jm>=e^{-i\alpha m'}<j,m'|e^{-i\beta J_2}|j,m>e^{-i\gamma m}\]这里也可以看出为什么量力/群论教材会使用y轴作为中间转动轴,因为这可以使中间e指数上为实数
仅需考虑中间的内积,记作$d^j(\beta)^{m’}_{~m}$,使用泰勒展开,注意到$-iJ_2=\frac{1}{2}(1,0;0,-1)$,偶数次幂恰为$\frac{1}{2^n}I$,将奇偶分别收集起来
\[d^{j=1/2}(\beta)^{m'}_{~m}=<j,m'|e^{-i\beta J_2}|j,m>=\delta^{m'}_{~m}cos\frac{\beta}{2}-i(\sigma_2)^{m'}_{~m}sin\frac{\beta}{2}\]写作矩阵形式即为
\[d^{\frac{1}{2}}(\beta) =\begin{pmatrix} cos\frac{\beta}{2}&-sin\frac{\beta}{2}\\ sin\frac{\beta}{2}&cos\frac{\beta}{2} \end{pmatrix}\]当j=1时,可算出
\[d^1(\beta)=\begin{pmatrix} (1+cos\beta)/2&-sin\beta/\sqrt 2&(1-cos\beta)/2\\ sin\beta/\sqrt 2&cos\beta&-sin\beta/\sqrt 2\\ (1-cos\beta)/2&sin\beta/\sqrt 2&(1+cos\beta)/2 \end{pmatrix}\]
回代到总旋转中,有
\[D^\frac{1}{2}(\alpha\beta\gamma)=\begin{pmatrix} e^{-i\alpha/2}cos\frac{\beta}{2}e^{-i\gamma/2}&e^{-i\alpha/2}-sin\frac{\beta}{2}e^{i\gamma/2}\\ e^{i\alpha/2}sin\frac{\beta}{2}e^{-i\gamma/2}&e^{i\alpha/2}cos\frac{\beta}{2}e^{i\gamma/2} \end{pmatrix}\]这样的矩阵保SO(3)的乘法关系易验证,现在取α=β=0,观察绕3轴转动下的矩阵
\[D^\frac{1}{2}(00\gamma)=\begin{pmatrix} e^{-i\gamma/2}&\\ &e^{i\gamma/2} \end{pmatrix}\]注意到这个矩阵并不是以2pi作为周期,而是4pi作为周期,这使得同一个转动对应两个矩阵,所以j=1/2时不能成为表示
为什么呢,不妨计算一下任意j下的绕3轴转动pi对应的矩阵
\[D^j[R_3(2\pi)]^{m'}_{~m}=\delta^{m'}_{~m}e^{-im2\pi}\]可见,若m是半奇数,则同一个转动对应两个矩阵,不是表示;若m是正整数,则$D^j$是不可约表示(证明见下文)
计算转角为γ时的特征标(下求和式可以看作等比数列求和)
\[\chi^j_\varphi=\sum_{m=-j}^je^{-im\varphi}=e^{-ij\varphi}\frac{e^{i\varphi(2j+1)}-1}{e^{i\varphi}-1}=\frac{e^{i\varphi(j+1/2)}-e^{-i\varphi(j+1/2)}}{e^{i\varphi/2}-e^{-i\varphi/2}}=\frac{sin[(j+1/2)\varphi]}{sin[\varphi/2]}\]定理1.2:当j为整数或半奇数且有限时,so(3)的如下表示是不可约表示
\[J_1 =\frac{1}{2}\begin{pmatrix} 0&1&&\\ 1&0&1&\\ &1&\ddots&1\\ &&1&0 \end{pmatrix};J_2 =\frac{1}{2}\begin{pmatrix} 0&-i&&\\ i&0&-i&\\ &i&\ddots&-i\\ &&i&0 \end{pmatrix};J_3 =\begin{pmatrix} j&&&\\ &j-1&&\\ &&\ddots&\\ &&&-j \end{pmatrix}\]警钟长鸣:J1 J2里面的非零分量不一定全是1,i这样漂亮统一的数,他要根据归一化系数改变!尽管如此,只需知道此处有非零数即可,证明无需用到他们具体是什么数
证明:观察J3,其特征向量正是基矢,且无简并现象,这告诉我们如果该表示的非0不变子空间W一定可以被某些基矢张成(原因同引理1.1中的有简并证明)。任取$ket{j,i}\in W$
将J1作用于上,得到$J_1\ket{j,i}=\frac{1}{2}(\ket{j,i-1}+\ket{j,i+1})$;反复作用后,所得的向量必可以张成全空间,也即该表示没有非平凡不变子空间,是不可约表示
定理1.3(男神yqy学长教我的):若李代数到李群的指数映射为满射,则李代数的不可约表示通过指数映射给出的李群的线性变换形式,如果是表示则一定是不可约表示
证明:反证若李群表示可约,则在适当的基下一定可以写作分块对角的形式,由李代数的求导式
\[X_a=i\frac{\partial}{\partial\alpha_a}D(\alpha)|_{\alpha=0}\]可得,生成元也是分块对角形式;对所有李群元作此求导操作后发现李群整体可以写作分块对角形式,这与李代数不可约的条件矛盾
由定理1.2和1.3可知,本节及上一节所使用的找表示的方法,当j为整数时确实给出了so(3)与SO(3)的不可约表示;而当j为半奇数时,给出了so(3)的不可约表示
由于李代数只蕴含了运算相关的信息,丢失了拓扑信息,所以so(3)可以同时对应不同构的李群SU(2)与SO(3);从so(3)导出的表示保证了运算上的同态,却不能保证拓扑信息的对应。
不可约波函数
先来复习一下前面讲过的“群表示作用在线性函数上”:设群元对应的线性变换是A,对于一个给定的关于坐标的线性函数f(x),a作用在f上的效果是:
\[Af(x)=f_a(x)=f(Ax)\]下面我们所要探讨的,旋转作用在波函数上,就与此类似
旋转的基础定义:作用在坐标矢上
\[U[R]|\vec x>=|R\vec x>\]| 取任一态函数$ | \psi>$,将其在坐标下展开 |
将U[R]作用于此,同时将$\braket{\vec x}{\psi}$记作$\psi(\vec x)$
\[U[R]|\psi>=\int U[R]|\vec x>\psi(\vec x)d^3x=\int |R\vec x>\psi(\vec x)d^3x=\int |\vec x>\psi(R^{-1}\vec x)d^3x\]其中,最后一个等号用到了积分换元,且由于旋转故雅可比行列式为1,可见旋转作用在波函数上的效果为
\[\psi(\vec x)\to\psi(R^{-1}\vec x)\]满足这样变化方式的波函数被称作不可约波函数;将其推广到向量场的情况:
\[\phi^m\to{\phi'}^m(\vec x)=D^j[R]^m_{~~n}\phi^n(R^{-1}\vec x)\]SO(3)直积表示的直和分解
脉络:注意是在李群SO(3)上作直积,所以在李群上整体表现出乘性,在so(3)上整体表现出加性;直积时考虑的是两个j形(就是通过上面那一套算出的)表示,所以直和的时候仍然考虑j形表示(至少是在同构意义下)
本节相当于是之前的“直积表示”节在SO(3)上的应用,回顾一下直积表示作用在直积矢量上的运算律(表示A所在表示空间有矢量a,表示B所在的表示空间有矢量b)
\[(A\otimes B)·(a\otimes b)=(Aa)\otimes(Bb)\]现在有SO(3)的两个不可约表示$D^j(R)$和$D^{j’}(R)$,对应的张量表示空间矢量$\ket{j,m}\otimes\ket{j’,m’}$记作|m,m’>,则他们的张量表示作用在张量后矢量上的运算律为
\[U(R)|m,m'>=(D^j(R)\otimes D^{j'}(R))(|j,m>\otimes|j',m'>)=(D^j(R)|j,m>)\otimes(D^{j'}(R)|j',m'>)\]注意到|j,m>是原表示空间基矢,所以$D^j(R)\ket{j,m}$相当于取出含m的列向量;而这个列向量又可以在一套基矢{|j,n>}下按矩阵分量系数展开(对于表示j’同理),展开后可以得到
\[U(R)|m,m'>=(\sum_n |j,n>D^j(R)^n_m)\otimes(\sum_{n'} |j',n'>D^{j'}(R)^{n'}_{m'})\]反向使用直积表示运算律,可得
\[U(R)|m,m'>=\sum_n\sum_{n'}|n,n'>D^j(R)^n_mD^{j'}(R)^{n'}_{m'}\]定理1.4:直积能形成表示(群元到矩阵一对一)<=>j+j’是正整数
证明:j与j’同为整数时易得,且j与j’一个为整数一个为半奇数时会一对二,所以仅需证j与j’同为半奇数时一对一
由于同角度转动,无论绕什么轴,都在同一个共轭类内;且j为半整数时矩阵周期为4pi,所以考虑绕3轴多旋转2pi后多出来的矩阵直积
\[U(R(2\pi))=\begin{pmatrix} e^{-2ij\pi}&&&\\ &e^{-2i(j-2)\pi}&&\\ &&\ddots&\\ &&&e^{2ij\pi} \end{pmatrix}\otimes\begin{pmatrix} e^{-2ij'\pi}&&&\\ &e^{-2i(j'-2)\pi}&&\\ &&\ddots&\\ &&&e^{2ij'\pi} \end{pmatrix}\]由于这是两个对角阵的张量积,故在求和式$\sum_n\sum_{n’}\ket{n,n’}D^j(R)^n_mD^{j’}(R)^{n’}_{m’}$仅有$(n,n’)=(m,m’)$的项非零,故
\[U(R(2\pi))|m,m'>=|m,m'>D^j(R)^m_mD^{j'}(R)^{m'}_{m'}\]另一方面,注意到两个矩阵e指数上所带的均为$i\pi$的奇数倍,矩阵分量相乘后得到e指数所带$i\pi$的偶数倍,即为1;由于|m,m’>选取的任意性,可知$U(R(2\pi))$的作用是单位映射,也即j与j’同为半奇数时群元到矩阵一对一
定理1.5:若jj’非0,则直积表示可约
证明:见本节下面,构造直和分解处
定理1.5对应例子:考虑j=j’=1/2,则$\ket{a}=\ket{\frac{1}{2},-\frac{1}{2}}-\ket{-\frac{1}{2},\frac{1}{2}}$
带上面公式就行了,不放心可以像我一样用最原始的运算律推一遍
小转动近似下的直积
\[(I^j-i\phi J_n^j)\otimes(I^{j'}-i\phi J_n^{j'})=I^{j\times j'}-i\phi(J_n^j\otimes I^{j'}+I^j\otimes J_n^{j'})\]故直积小转动生成元为
\[J^{j\times j'}_n=J_n^j\otimes I^{j'}+I^j\otimes J_n^{j'}\]直积表示生成元的谱恰为表示j与表示j’谱的和,以n=3为例
\[J^{j\times j'}_3|m,m'>=(J_3^j\otimes I^{j'}+I^j\otimes J_3^{j'})|m,m'>\\=(J_3^j|j,m>)\otimes(I^{j'}|j',m'>)+(I^j|j,m>)\otimes(J_3^{j'}|j',m'>)=(m+m')|m,m'>\]为了寻找直积表示在$D^j$类表示上的直和分解,也就是要寻找新基,使表示矩阵分块对角化;而在构造$D^j$类表示时,我们将上升下降算符反复作用于基矢上,迭代出全套基矢;所以在这里我们不妨先取一个最“高”的张量矢量$\ket{j,j’}$,将张量表示中新的J-算符作用于上
\[J^{j\times j'}_-=J_-^j\otimes I^{j'}+I^j\otimes J_-^{j'}\]重点不在归一化系数上,所以为方便,记归一化系数$c(j,m)=\sqrt{j(j+1)-m(m-1)}$
\[J^{j\times j'}_-\ket{j,j'}=c(j,j)\ket{j-1,j'}+c(j',j')\ket{j,j'-1}\] \[J^{j\times j'}_-(J^{j\times j'}_-\ket{j,j'})\\ =c(j,j-1)c(j,j)\ket{j-2,j'}+2c(j',j')c(j,j)\ket{j-1,j'-1}+c(j',j'-1)c(j',j')\ket{j,j'-1}\] \[...\]以此类推,可见当$J^{j\times j’}_-$作用k次时,得到的矢量是所有形如$\ket{n,m},(j+j’)-(n+m)=k;n\in[-j,j],m\in[-j’,j’]$的矢量的线性组合(也有一点像二项式展开的形式)
换言之,给定任意的直积表示空间基矢|n,m>,总可以通过(j+j’)-(n+m)来判断这个矢量会在J-作用于|j,j’>几次后出现。也即,我们借助下降算符的作用次数给出了直积空间基矢的一个划分
| 在寻找有限维不可约表示时,我们人为地将上升下降算符的作用序列进行了截断;所以在这里我们也需要关注下降算符作用到何时停止,幸运的是,由于张成新基矢的两个原基矢的m值均有界,张成的 | j,j’>所能承受的最大次数下降为j+j’ |
现在我们就可以按J3作用次数(下降次数)给直积表示空间基矢做一个有限划分
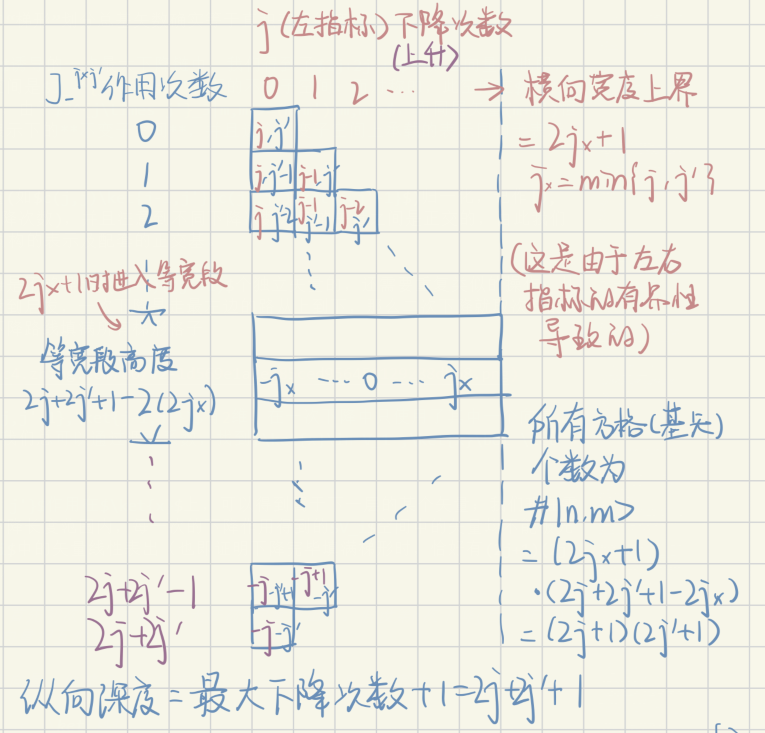
在右下角核验了这样的“梯形”划分总基矢数确实等于直积表示维度。
在$J_-^{j\times j’}$诱导的一次最大下降链中,我们得到了$2j+2j’+1$个独立向量;也即,由此下降链张成的子空间是$J_-^{j\times j’}$下的不变子空间;而对称的,此空间在$J_+^{j\times j’}$下不变;由于$J^{j\times j’}_3\ket{m,m’}=(m+m’)\ket{m,m’}$,而同层矢量(m+m’)恒定,故该空间是直积表示下的不变子空间,并且这个不变子空间上承载的表示同构于表示$D^{j+j’}$
将下降链上的所有矢量(如$c(j,j)\ket{j-1,j’}+c(j’,j’)\ket{j,j’-1}$)归一化,记作|J,J-i>(J=j+j’,i表示下降次数),并且注意到不同下降次数对应的矢量之间是正交的,由此我们分离出与$D^{j+j’}$同构的表示及配套的正交基。
很明显单条最大下降链是不够导出$(2j+1)(2j’+1)$个独立矢量的,还需要重复类似的操作;从上面的矢量划分图中受到启发,一次下降是走最左边的路从上到下,那么二次下降就取次左的纵路,以此类推,直到下降路线填满所有梯形格子
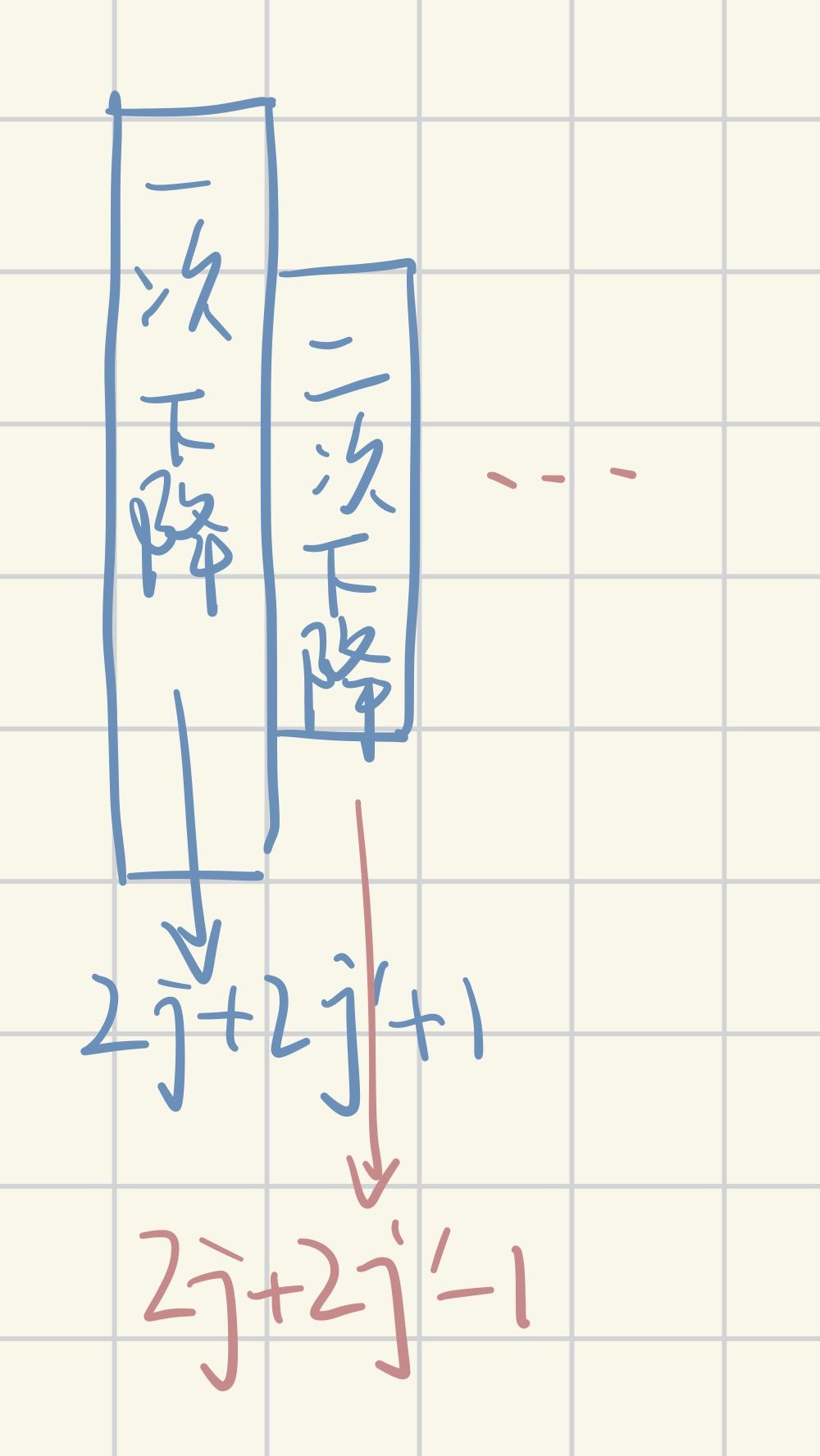
由于$V_1=span(\ket{j,j’-1},\ket{j-1,j’})$有2维,在一次下降中只使用了其中一个向量$\ket{J,J-1}$,所以我们总可以通过调配系数,找到$\ket{x}\in V_1 ;\ket{x}\bot \ket{J,J-1},|x|=1$
同理用$J_-^{j\times j’}$作用在$\ket{x}$上,可以得到属于下一层的某个矢量;我们现在需要证明的是,在最大下降长度范围内,每一次的下降作用得到的$V_i$空间中的矢量均不能被先前所有下降得到的$V_i$中的矢量线性表出(也即证明下降完毕填满梯形时,恰好有(2j+1)(2j’+1)个线性无关的向量)
证明:利用归纳法,先考虑无损失下降,即一次扩展恰好使用到的张量基矢+1;首先初次下降时必然是无法被0向量表出的。假设第k次下降(J-作用k次层)时,本空间中前k-1个向量相互独立
观察本轮下降的最高向量,他被定义为与前k-1个向量均相互垂直;设其为
\[\ket{k,1}=\sum_{i=0}^k a_i\ket{j-i,j'-(k-i)}\]受到一次$J_-^{j\times j’}$的下降作用后,变为
\[J_-^{j\times j'}\ket{k,1}=\\\sum_{i=0}^k a_i(c(j,j-i)\ket{j-i-1,j'-(k-i)}+c(j',j'-(k-i))\ket{j-ij'-(k-i)-1})\\:=\sum_{i=0}^{k+1} b_i\ket{j-i,j'-(k+1-i)}\]不妨用矩阵形式描述下降过程
\[\begin{pmatrix} c(j',j'-k)&&&\\ c(j,j)&c(j',j'-k+1)&&\\ &c(j,j-1)&\ddots&\\ &&&c(j',j')\\ &&&c(j,j-k) \end{pmatrix} \begin{pmatrix} a_0\\ a_1\\ ...\\ a_k \end{pmatrix}=\begin{pmatrix} b_0\\ b_1\\ ...\\ b_{k+1} \end{pmatrix}\]其中,左侧的矩阵有k+1行,k+2列;除去最下一行后变为下三角方阵,由于现在考虑无损失下降,故对角线元素全部非0,方阵行列式不为0,也即矩阵有k+1维;考虑多个向量并行处理的情况:
\[\begin{pmatrix} c(j',j'-k)&&&\\ c(j,j)&c(j',j'-k+1)&&\\ &c(j,j-1)&\ddots&\\ &&&c(j',j')\\ &&&c(j,j-k) \end{pmatrix} \begin{pmatrix} a_0&a'_0&...\\ a_1&a'_1&...\\ ...\\ a_k&a'_k&... \end{pmatrix}=\begin{pmatrix} b_0&b'_0&...\\ b_1&b'_1&...\\ ...\\ b_{k+1}&b'_{k+1}&... \end{pmatrix}\]当系数a所在的矩阵秩=列数时,由于左乘的矩阵也是“列数满秩”的,所以系数b所在矩阵同样秩=列数,也即下降算符同时作用在一组线性无关的矢量后(若J-归一化系数均非零),仍然导出一组线性无关矢量
而在损失下降的情况下(自2jx以后的所有下降),左侧或为下三角矩阵,或为行数小于列数的瘪双对角矩阵,处理方法同上,都可以算出是保至多rank个的线性无关性(这个方法也可以导出下降至梯形区域外就保不了线性无关了)
进一步证明:通过这种方法得出的新基必是彼此间正交的,且是一个对称矩阵的本征矢,请见附录1
有关不变子空间上新上升下降算符的自洽性,参见附录2
如果附录2得到证明,那么不变子空间上的上升下降算符与期望构造的直和表示分量同构;进一步,由于J3在每一层上退化为标量,也即J3是同构的;证出三个独立同构矢量后,其他均可以推出同构关系,这种直和分解的有效性得到一个好的证明。
至此,我们证明了按照上述方法依次下降,就可以得到(2j+1)(2j’-1)个独立矢量,以及定义在其上的直和表示分解$\bigoplus_{i=2|j-j’|+1}^{2(j+j’)+1} D^i$
SU(2)
定义:2x2酉矩阵,特征值为1
可以看出SU(2)一共有3个实变量,用这个约束可以造一个参数化
\[\begin{pmatrix} cos\theta e^{i\zeta}&-sin\theta e^{i\eta}\\ sin\theta e^{-i\eta}&cos\theta e^{-i\zeta} \end{pmatrix}\]将其与之前造出的SO(3)双值表示对比,发现该双值表示恰为SU(2)的一个合法表示
\[D^\frac{1}{2}(\alpha\beta\gamma)=\begin{pmatrix} e^{-i\alpha/2}cos\frac{\beta}{2}e^{-i\gamma/2}&e^{-i\alpha/2}-sin\frac{\beta}{2}e^{i\gamma/2}\\ e^{i\alpha/2}sin\frac{\beta}{2}e^{-i\gamma/2}&e^{i\alpha/2}cos\frac{\beta}{2}e^{i\gamma/2} \end{pmatrix}\] \[\theta =\frac{\beta}{2}\in[0,\frac{\pi}{2}]~;~\zeta=-\frac{\alpha+\gamma}{2}~;~\eta=\frac{-\alpha+\gamma}{2}\] \[\alpha\in[0,4\pi)~;~\gamma\in[0,2\pi)\]另一种参数化
\[\begin{pmatrix} r_0-ir_3&-r_2-ir_1\\ r_2-ir_1&r_0+ir_3 \end{pmatrix}\]要附上条件$r_0^2+r_1^2+r_2^2+r_3^2=1$,可以看出SU2的几何结构是一个四维球面
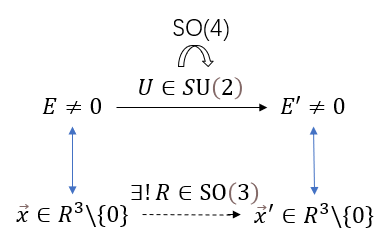
SU(2)与SO(3)的对应
观察:SU(2)在2x2无迹厄米矩阵上的相似作用
设有2x2的无迹厄米矩阵E,则E可以参数化写作
\[E(x_1,x_2,x_3)=\begin{pmatrix} x_3&x_1-ix_2\\ x_1+ix_2&-x_3 \end{pmatrix}\]平行地,无迹2阶厄米矩阵可以写作三个泡利矩阵的线性组合
还是三个独立参数,所以记$\vec x=x_1\vec i+x_2\vec j+x_3\vec k$
\[E(\vec x)=x_1\begin{pmatrix} &1\\ 1& \end{pmatrix}+x_2\begin{pmatrix} &-i\\ i& \end{pmatrix}+x_3\begin{pmatrix} 1&\\ &-1 \end{pmatrix}=x_1\sigma_1+x_2\sigma_2+x_3\sigma_3=\begin{pmatrix} x_3&x_1-ix_2\\ x_1+ix_2&-x_3 \end{pmatrix}\]也即,无迹2阶厄米矩阵和一个3维(实)矢量建立了一对一的联系
下面将$U\in SU(2)$相似作用在E上,得到
\[E'=UEU^{-1}~~\Rightarrow(E')^\dagger=U^{-\dagger}E^\dagger U^\dagger=UEU^{-1}=E'\] \[tr(E')=tr((UU^{-1})E)=tr(E)=0\] \[det(E)=-(x_1^2+x_2^2+x_3^2)\] \[det(E')=det(E)=-(x_1^2+x_2^2+x_3^2)\]也即,作用后的E’也是无迹2阶厄米矩阵,它也对应一个三维矢量$\vec x’$(而且$\norm{x}=\norm{x’}$);那么很自然地可以想到,因为SO(3)的作用也是将一个三维矢量保长度地打到另一个三维矢量上,所以或许SU(2)与SO(3)有着平行的作用
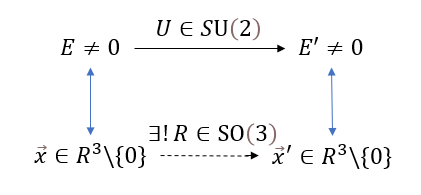
下面我们来验证通过这个方式将SU(2)中元素送到SO(3)中元素的映射$\phi:SU(2)\to SO(3)$使得$UE(\vec x)U^{-1}=E(\phi(U)\vec x)$是同态映射
主要用到的性质是相似变换的结合律,对于$U_1U_2EU_2^{-1}U_1^{-1}$,既可以看作是$U_1U_2$一起作用后得到$(U_1U_2)E(U_1U_2)^{-1}$,此时$\vec x$受到的旋转变换是$\phi(U_1U_2)$;分开看时,E分两次受到不同的相似变换,x也一样,最后x变为$\phi(U_1)\phi(U_2)$,也即$\phi(U_1U_2)=\phi(U_1)\phi(U_2)$
下面证φ满射,重头戏来咯
比较有趣,除了要合理用到所有条件以外,还可以巨大玩线代
设$\forall R\in SO(3)$,证明存在U,使得$\phi(U)=R$.
2阶厄米矩阵E必然存在两个实特征值,由于tr(E)=0,可知两个特征值反号,设他们为$\pm\lambda_1$,同理设变化后的E’的特征值为$\pm\lambda_2$,由$det(E)=det(E’)$,可得
\[-\lambda_1^2=-\lambda_2^2\Rightarrow\lambda_1=\pm\lambda_2\]也即,变化前后E的谱不变,记E和E’的谱为$\pm\lambda_1,\lambda_1>0$
由于E和E’均为厄米矩阵,所以存在正交归一基,设E的正特征值对应的归一特征向量为$\vec x_1$,E的负特征值对应的归一特征向量为$\vec x_2$,E’的正特征值对应的归一特征向量为$\vec x_3$,E’的负特征值对应的归一特征向量为$\vec x_4$,则可以写作
\[E=\begin{pmatrix} \vec x_1&\vec x_2\\ \end{pmatrix}\begin{pmatrix} \lambda_1&\\ &-\lambda_1 \end{pmatrix}\begin{pmatrix} \vec x_1^\dagger\\ \vec x_2^\dagger \end{pmatrix}\]谱全同的矩阵相差相似变换,而谱全同的厄米矩阵相差正交相似变换,该变换为
\[U=\begin{pmatrix} \vec x_3&\vec x_4\\ \end{pmatrix}\begin{pmatrix} \vec x_1^\dagger\\ \vec x_2^\dagger\\ \end{pmatrix}\] \[E'=UEU^{-1}\]正交性
\[UU^\dagger=\begin{pmatrix} \vec x_3&\vec x_4\\ \end{pmatrix}\begin{pmatrix} \vec x_1^\dagger\\ \vec x_2^\dagger\\ \end{pmatrix}\begin{pmatrix} \vec x_1&\vec x_2\\ \end{pmatrix}\begin{pmatrix} \vec x_3^\dagger\\ \vec x_4^\dagger\\ \end{pmatrix}=I\]埋一个伏笔,观察到这里的U如果全部分量都填上一个负号,那么这一套仍然成立,也即$\pm U$具有同样的联系厄米矩阵的作用
至此,我们证明了φ是一个同态映射,现在考虑一下同态核,也即平凡的相似变换
\[\forall E\ne 0,E^\dagger=E,tr(E)=0,U\in SU(2);~UEU^{-1}=E\Rightarrow U=\pm I\] \[ker(\phi)=\pm I\simeq Z_2\]由$im\phi(A)\simeq A/ker\phi$,可得
\[SO(3)\simeq SU(2)/Z_2\]所以称SU(2)是SO(3)的双覆盖
su(2)与so(3)的结构
下面求一下su(2)的生成元,使用r参数化
\[\begin{pmatrix} r_0-ir_3&-r_2-ir_1\\ r_2-ir_1&r_0+ir_3 \end{pmatrix}\]单位元是$r_0=1$,$r_1=r_2=r_3=0$,现在给$r_1$一个无穷小微扰,(忽略高阶无穷小后)$r_0=1,r_1=\epsilon$,矩阵变为
\[\begin{pmatrix} 1&-i\epsilon\\ -i\epsilon&1 \end{pmatrix}=I-i\sigma_1\epsilon\]也即参数r1对应的生成元是泡利矩阵$\sigma_1$,同理可以算出r2、r3分别对应$\sigma_2$、$\sigma_3$,也可以算泡利矩阵的对易关系$[\sigma_k,\sigma_l]=2i\varepsilon_{klm}\sigma^m$
将所有泡利矩阵每个分量同除2,得到的新生成元运算律与so(3)生成元完全一致,所以我们说su(2)=so(3),以后(也许可以)不加区分
SU(2)的不可约表示
前情提要:在找so(3)的不可约表示时,我们遍历J3本征值m,利用本征矢张成表示空间基,用j表明最大特征值;在这里,我们将m换做$\mu$,通过遍历$\mu$生成一系列函数,通过矩阵作用在函数上的效果来给出表示
使用一种崭新的复数参数化描述SU(2)中的元素
\[U=\begin{pmatrix} a&b\\ -b^*&a^* \end{pmatrix}\]其中,ab均为复数,且式中没有体现的约束是a的模长与b模长的和为1
构造关于$\vec x=(x_1,x_2)$的齐次单项式(下面那个根号起到归一化系数的作用)
\[\eta_\mu(\vec x)=\frac{x_1^{j+\mu}x_2^{j-\mu}}{\sqrt{(j+\mu)!(j-\mu)!}},\mu=-j,-j+1,...,j-1,j\]定义$U\in SU(2)$作用在$\eta_\mu(\vec x)$上的效果(和之前的函数表示差不多)
\[(U\eta_\mu)(\vec x)=\eta_\mu'(\vec x)=\eta_\mu(U\vec x)=\frac{(ax_1+bx_2)^{j+\mu}(-b^*x_1+a^*x_2)^{j-\mu}}{\sqrt{(j+\mu)!(j-\mu)!}}\]这个东西可以用已定义的{$\eta_\mu$}展开(j是表示的标号)
\[\eta_\mu'(\vec x)=\sum_{\mu=-j}^jA_{\mu\nu}^j(U)\eta_\nu\]其中,展开系数$A_{\mu\nu}^j(U)$为
\[A_{\mu\nu}^j(U)=\sum_{k=max\{0,\mu-\nu\}}^{min\{j-\nu,j+\mu\}}\frac{(-1)^{k-\mu+\nu}\sqrt{(j+\mu)!(j-\mu)!(j+\nu)!(j-\nu)!}}{k!(j-\nu-k)!(j+\mu-k)!(k-\mu+\nu)!}a^{j+\mu-k}a^{*j-k-\nu}b^kb^{*k-\mu+\nu}\]展开系数的计算:这比想象中的简单太多,就是两个二项式的积
将$\eta_\mu’(\vec x)$的分母展开为两个二项式积的形式
\[(ax_1+bx_2)^{j+\mu}(-b^*x_1+a^*x_2)^{j-\mu}=(\sum_{k=0}^{j+\mu}C_{j+\mu}^k(ax_1)^{j+\mu-k}(bx_2)^k)(\sum_{i=0}^{j-\mu}C_{j-\mu}^i(-b^*x_1)^{j-\mu-i}(a^*x_2)^i)\]现在来看这个式子里面$x_1^{j+\nu}x_2^{j-\nu}$项的系数,利用$x_2$的幂次做限制条件,令$i=j-\nu-k$,则后面二项式对幂次的上下界控制为
\[0\le \nu-\mu+k\le j-\mu\]解得
\[\mu-\nu\le k\le j-\nu\]故$x_1^{j+\nu}x_2^{j-\nu}$项的系数为
\[\sum_{k=max\{0,\mu-\nu\}}^{min\{j-\nu,j+\mu\}}C_{j+\mu}^kC_{j-\mu}^{j-\nu-i}a^{j+\mu-k}a^{*j-\nu-k}b^k(-b^*)^{\nu-\mu+i}\]考虑$\eta_\nu$与$\eta_\mu’(\vec x)$的归一化系数,得到展开系数为
\[A_{\mu\nu}^j(U)=\sum_{k=max\{0,\mu-\nu\}}^{min\{j-\nu,j+\mu\}}C_{j+\mu}^kC_{j-\mu}^{j-\nu-i}a^{j+\mu-k}a^{*j-\nu-k}b^k(-b^*)^{\nu-\mu+i}\sqrt{\frac{(j+\nu)!(j-\nu)!}{(j+\mu)!(j-\mu)!}}\]将组合数打开即可得到命题的形式,得证
连续性表示分量正交归一定理
前情提要:在有限群中探讨了表示矩阵分量诱导向量组的正交归一性,在李群内需要将求和号改为积分;由于积分测度必须与重排引理自洽,所以必须给出一个重排下不变的测度来进行积分。
先把离散的正交公式复制过来以便随时查
\[\frac{n_\mu}{n_G}\sum_gD^\dagger_\mu(g)^k_iD^\nu(g)^j_l=\delta_\mu^\nu\delta_i^j\delta_l^k\]记被积函数为f(A)(对标$D^\dagger_\mu(g)^k_iD^\nu(g)^j_l$),使用r参数化构造积分式,将限制条件$\sum r^2=1$加入,则有
\[\int\delta(1-\sum r^2)dr_0dr_1dr_2dr_3dr_4f(A)\]首先验证测度的重排不变性,也即将这一组参数统一换成任意群元对应的另一组参数r’,求雅可比行列式
\[\frac{\partial(r_0',r_1',r_2',r_3')}{\partial(r_0,r_1,r_2,r_3)}\]注意到限制条件$r_0^2+r_1^2+r_2^2+r_3^2=1$,SU(2)群元与四维球面一一对应,而SO(4)恰将四维球面上长度为1的矢量联系起来,所以雅可比行列式在求的是SO(4)内群元的行列式,为1
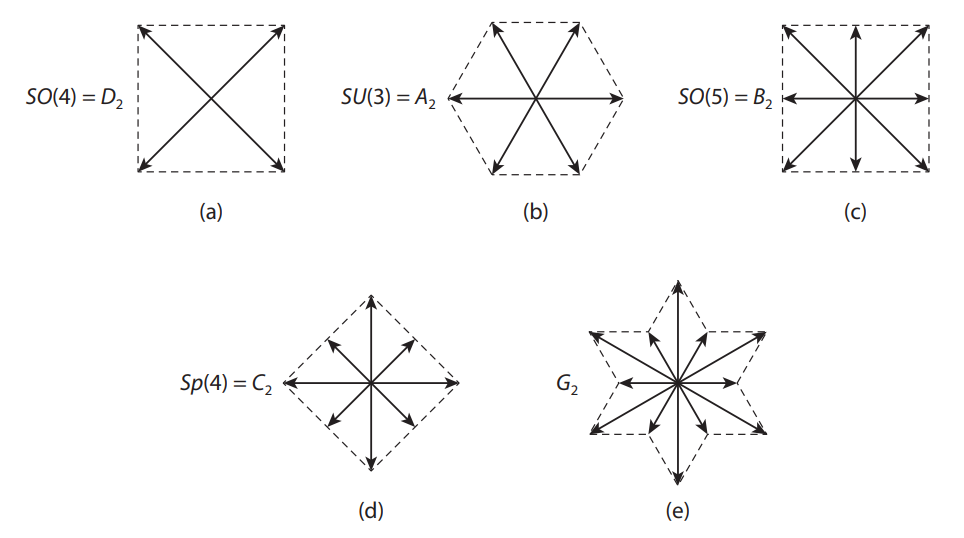
支线:所以先前的图可以再加一点
至此,我们找到了在重排下不变的群元参数积分测度,下面的任务就是想办法去掉限制$\delta(1-\sum r^2)$,以达到三参数描述的形式;考虑之前的角度参数化
\[\begin{pmatrix} cos\theta e^{i\zeta}&-sin\theta e^{i\eta}\\ sin\theta e^{-i\eta}&cos\theta e^{-i\zeta} \end{pmatrix}\]打开,对比换元;为了消去长度1的限制条件,在每个参数前加入了模长r
\[r_0=rcos\theta cos\zeta~~r_3=-rcos\theta sin\zeta\] \[r_2=rsin\theta cos\eta~~r_1=rsin\theta sin\eta\]则微分形式(不是那个微分形式)
通过雅可比行列式计算(其实我一开始应该直接列雅可比的)(4x4行列式,不过消一消空挺多)
\[dr_0dr_1dr_2dr_3=\frac{1}{2}r^3sin2\theta drd\theta d\eta d\zeta=\frac{1}{4}r^2 sin2\theta dr^2 d\theta d\eta d\zeta\]代入条件$\delta(1-r^2)$后化为
\[\frac{1}{4}sin2\theta d\theta d\eta d\zeta\]对比SO(3)的j=1/2表示,可以将这一套角度参数化转换为j=1/2表示参数化
\[\theta =\frac{\beta}{2}~;~\zeta=-\frac{\alpha+\gamma}{2}~;~\eta=\frac{-\alpha+\gamma}{2}\]积分微元化作
\[\frac{1}{16}d\alpha dcos\beta d\gamma\]也就是说,上面的工作找到了(在重排下不变的)$\sum_g$的连续形式(积分区域取得是SU(2))
\[\int_0^{2\pi}\int_1^{-1}\int_0^{4\pi}\frac{1}{16}d\alpha dcos\beta d\gamma\]但是在原离散正交式子中,有系数$1/n_G$,也就是对群元取平均的形式;在这里取平均时,SO(3)要(在上面的基础上)除$\pi^2/2$,SU(2)要除$\pi^2$(直接取权1自己积分),除掉之后得到归一化不变测度(以SU(2)为例),记作$d\tau$
\[d\tau=\int_0^{2\pi}\int_1^{-1}\int_0^{4\pi}\frac{1}{16\pi^2}d\alpha dcos\beta d\gamma\]那么就可以写出连续形式的正交定理
\[(2j+1)\int d\tau D_j^\dagger(A)^i_mD^{j'}(A)^l_k=\delta^{j'}_j\delta^i_k\delta^l_m\]有了这个公式,就可以求完备性展开中的系数了;对于群元的函数f(A),都可以通过矩阵分量展开
\[f(A)=\sum f_{jm}^n D^j(A)^n_m\]两边代入正交性积分表达式,得
\[f^n_{jm}=(2j+1)\int d\tau_A D^\dagger_j(A)^n_mf(A)\]完备性定理的连续性表述
\[(2j+1)\sum_{jmn}D^j(A)^m_nD^\dagger_j(A)^n_m=\delta(A-A')\]一般矩阵李代数表示
本章讲的找表示的方法在马中骐的《物理学中的群论》和《Lie Algebras in Particle Physics》有写
写在前面:关于幺正与厄米的联系
在先前有限群表示中,我们证明了所有有限维表示均与一个幺正表示等价,所以仅需研究幺正的有限表示;但是在李代数表示中我们希望表示是厄米的(有没有一个定理说明哪些李代数必然可以与厄米表示等价?我没看到)在这里给一个令人踏实的小证明
令d->0,在I附近展开李群元素
\[e^{-idX}=I-idX\]若李群幺正,则有$e^{-idX}(e^{-idX})^*$,即
\[(I-idX)(I+idX^\dagger)=I\]略去高阶小量后有$X=X^\dagger$,这就是我们要的厄米
(个人理解)在量子力学中由于要保证变换前后全概率保持为1,所以要求平移类算符的幺正性,进而可以推出这些算符对应生成元的厄米性
在先前的so(3)表示中,我们用J3和J方的本征矢张成基,再用组合而成的$J_\pm$来升降基;扩展到一般矩阵李代数中,将$J_3$(与$J^2$)这样的对易厄米算符拓广到集合{$H_i$},余下算符通过组合形成数对升降算符{$E_{\pm\alpha}$}(α是用来标注E的一个向量,其含义在下面会解释)
注意1:在su(2)中我们研究的等效生成元实际上只有3个:J3、J正负;也就是说{$H_i$}中只有J3这一个元素(我把J方拉出来是想说对易性)
注意2:收集Hi的细节。上面没能表述好,过程就是你把所有厄米且对易的算符先收集起来。1.若现有的Hi利用特征值完全划分全空间为一些一维子空间(无简并)此时若有一个非厄米的算符在Hi外面,则该非厄米算符必然不可能与全部Hi对易,此时Hi代表最大对易子代数;2.若现有的Hi仍有简并(两个不共线矢量拥有同一套特征值),则任意一个与{Hi}共享不变子空间的算符均可与{Hi}全体对易。这种情况(可能)以后考虑
注意3:在这里我们隐含了一个假定:对于所有李代数,寻找一个最大对易子代数,剩下的生成元通过线性组合,必定可以生成一些等数目的上升下降算符
这个隐含条件在伴随表示(下一节)得到证明
注意4:关于Hi的厄米性。由于Hi中生成元互相对易,所以可以做到同时对角化
{$H_i$}中的元素满足两两作李括号后均为0,可以看出他们构成了李代数的子代数,称其为嘉当(Cartan)子代数,其中独立生成元的数目称为原(母)李代数的rank
就像用J3的特征向量作为表示空间基矢一样,我们用嘉当子代数的特征矢作为空间基矢,写作
\[|\vec \mu,x,D>\]其中,μ向量的第i个分量代表Hi作用在它上面的特征值,被称作权矢量,x代表简并(如果不发生简并可以不管),D标注了表示;并且这样的矢量通过归一化使得长度为1
定理:在紧致李代数中,总可以对原有生成元{Yi}进行线性组合,使得新的一组生成元{Ti}的内积·满足:
\[T_i·T_j:=tr(T_iT_j)=\lambda\delta_{ij}\]前面一个等号是内积的定义,后一个等号说明了trace的正交性,比例系数λ取决于表示以及表示的归一过程(也就是说,在同一个确定的表示中λ是不变的)
证明:引入Cartan-Killing度规
\[g^{ij}=tr(Y^iY^j)\]注意到gij是对称矩阵,且有紧致李代数gij正定,故gij必与单位阵合同
对这一堆{Yi}执行待定的线性重组,生成一组{Ti},使得$T^i=P^i_jY^j$(对j求和),由于要求生成元Ti相互独立,所以线性变换矩阵P非退化,设S是P的逆,此时
\[tr(Y^iY^j)=tr(S^i_kT^kS^j_lT^l)\]由于矩阵S中的分量为标量,所以可以拿到tr外面
\[tr(Y^iY^j)=S^i_ktr(T^kT^l)S^j_l=S^i_ktr(T^kT^l)(S^T)^l_j\]写成矩阵形式即
\[g_Y=Sg_TS^T\Rightarrow g_T=Pg_YP^T\]总可以找到满足条件的P,使得在{Ti}下的Cartan-Killing度规是单位阵
伴随表示(对标有限群正则表示)
注意:只有半单李代数时构造的这个东西才能成为表示,因为$ad L\simeq L/Z(L)$
就像题目所说的,这个表示和有限群正则表示思路一致,只是把群作用改成了伴随作用$ad_X·=[X,·]$
将每个李代数生成元当作基矢,定义生成元对应的线性变换为
\[A|B>=|ad_AB>=|[A,B]>=\sum_C if_{abc}|C>\]并在其上定义内积
\[<A|B>=\lambda^{-1}Tr(A^\dagger B)\]其中,λ在前面被定义,它是由表示和归一化决定的
注意到:上升下降算符与厄米矩阵(标度上升下降的尺子)之间的李括号为上升下降算符的倍数(这是显然的,从上升下降的作用考虑,$HE\ket{x}=(EH+[H,E])\ket{x}$)
| 那么,任意|E>在任意H下均为特征矢量,所以可以很自然地设他们正交归一;用作标明$E_\alpha$的α向量(叫做根)便定义为伴随表示中 | Eα>所对应的权矢量。根矢量表明了上升下降算符在每个H下上升下降的效果和能力。 |
例:在su(2)中,$[J_3,J_\pm]=\pm J_\pm$,前面的特征值±1代表J±将J3下的特征升降1,J±的根α即为±1
预告:可以注意到,根α所在空间的维度恰为李代数的rank,所以至多有rank个独立的根。
定理:一对$\pm\alpha$仅对应一对$E_{\pm\alpha}$(不出现简并)
证明:可能比较麻烦所以不证了
还可以注意到,由于Hi之间互相对易,所以他们互在彼此的ker内,这未尝不是一种特征向量,所以Hi的权矢量均为0
下面进行一个神奇的操作,对H E的对易关系左右两侧取dagger
\[[H_i,E_{+\alpha}]=a_iE_{+\alpha}=H_iE_{+\alpha}-E_{+\alpha}H_i\Rightarrow a_iE_{+\alpha}^\dagger=E_{+\alpha}^\dagger H_i-H_iE_{+\alpha}^\dagger\] \[\Rightarrow[H_i,E_{+\alpha}^\dagger]=-\alpha_iE_{+\alpha}^\dagger\]这恰是$E_{-\alpha}$的定义,所以
\[E_{+\alpha}^\dagger=E_{-\alpha}\]提示:$E_{+\alpha}^\dagger$仍在表示中的必要条件是全部算符厄米
上面有了伴随表示中H在所有矢量下的作用,并且E作用在H>上与H|E>是对称的;所以下面来计算Ei|Ej>,就可以将伴随表示中所有作用关系搞清楚了
\[H_iE_{+\alpha}|E_{-\alpha}>=[H_i,E_{+\alpha}]|E_{-\alpha}>+E_{+\alpha}H_i|E_{-\alpha}>=\alpha_iE_{+\alpha}|E_{-\alpha}>-\alpha_iE_{+\alpha}|E_{-\alpha}>=0\]也即,$E_{+\alpha}\ket{E_{-\alpha}}\in ker H_i$,所以它可以被Hj线性表出,写作
\[E_{+\alpha}|E_{-\alpha}>=\sum_i \beta_i|H_i>\]| 由先前提到的Tr形式内积下H的正交归一性,要求展开系数β仅需左乘<Hi |
也即
\[E_{+\alpha}|E_{-\alpha}>=\sum_i \alpha_i|H_i>\Rightarrow[E_\alpha,E_{-\alpha}]=\vec \alpha ·\vec H\]总结:伴随表示这一节,与其说是找表示,不如说是利用我们熟悉的表示架构进一步研究了李代数内禀的性质
利用伴随表示证明一般矩阵李代数表示中的注意3:(仅证明全算符厄米或Hi非简并两者至少成立一种、且李代数半单的情况)
由于全算符厄米或Hi非简并两者至少成立一种,所以此时剩下的元素集合Ai中的元素不与Hi全体对易,{Hi}恰为最大对易厄米算符集合
利用Hi,Ai构建伴随表示,并配备上面介绍的迹内积。可以看出|Hi>构成的空间是每个Hj算符的核空间,也即不变子空间;由于半单李代数可约则可分解,故|Hj>张成空间的补空间|Ai>也是不变子空间(Hi中所有算符对易,所以自然可以同时(分块)对角化)
由于Hi是厄米的,直和分解去掉一个0矩阵,剩下的一定是厄米的,那么厄米算符下必定有一组正交的本征矢,他们是|Ai>的线性组合;也即,n个独立的Ai通过线性组合,必能拼出n个独立的上升下降算符
更进一步的,如果算符的表示是全厄米的,那么其正负特征值会成对出现,表现为$E_{+\alpha}^\dagger=E_{-\alpha}$
一些结构性质
根矢量的叠加
\[[H^i[E_\alpha,E_\beta]]=-[E_\beta[H^i,E_\alpha]]-[E_\alpha[E_\beta,H^i]]=-\alpha^i [E_\beta,E_\alpha]+\beta^i[E_\alpha,E_\beta]=(\alpha^i+\beta^i) [E_\alpha,E_\beta]\]也即,若Ea与Eb不对易,则他们的李括号生成了$E_{\alpha+\beta}$
我们将这条性质写作
\[[E_\alpha,E_\beta]=N_{\alpha,\beta}E_{\alpha+\beta}\]若LHS=0,则对应$N_{\alpha,\beta}=0$,可以看出N关于参数具有反对称性
根链
在有限维李代数中,根的数目是有限的,故根的上升下降链会在某一处截断
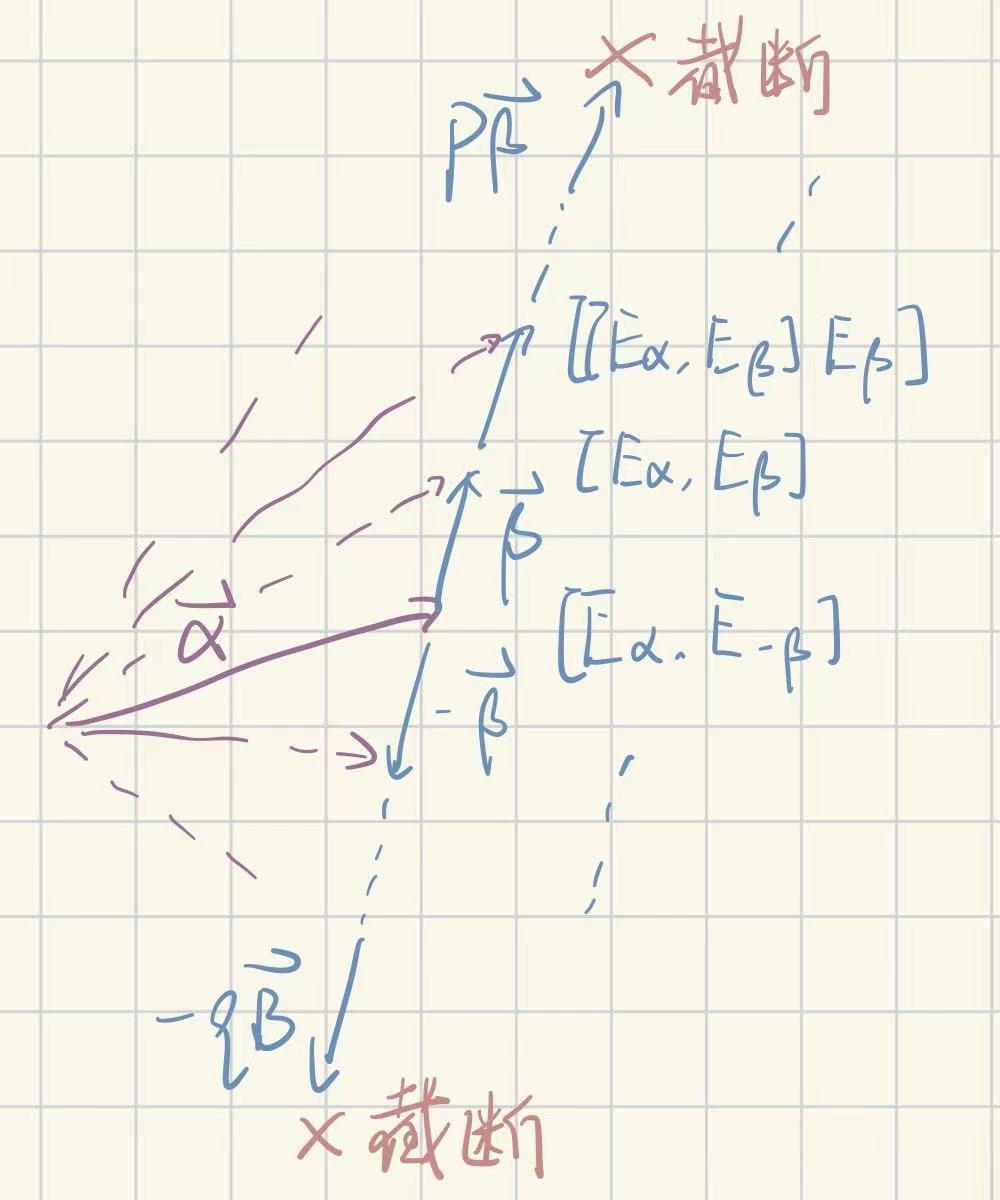
令
\[F_n=-N_{\alpha+n\beta,\beta}N_{(\alpha+(n+1)\beta),-\beta}\]也即n处上升下降一个来回改变的模长逆。(这是老朋友了啊,谐振子数目算符N也是上升下降一个来回凑出来的)则由最大上升下降极限,有
\[F_p=F_{-q-1}=0\]在n层楼做一个上升下降操作并用雅可比行列式写出来
\[0=[E_{\alpha+n\beta},[E_\beta,E_{-\beta}]]+[E_{\alpha+n\beta},[E_\beta,E_{-\beta}]]+[E_{\alpha+n\beta},[E_\beta,E_{-\beta}]]\\ =\{-\vec\beta·(\vec\alpha+n\vec\beta)-F_{n-1}+F_n\}E_{\alpha+n\beta}\]所以有Fn的递推关系(往后展开,外面系数beta不变,每开一次α多一个,然后里面的β是个等差数列)
\[F_n=F_{n-1}+\vec\beta·(\vec\alpha+n\vec\beta)=\frac{1}{2}(n+q+1)\vec\beta·[2\vec\alpha+(n-q)\vec\beta]\]当n=p时
\[2\vec\alpha·\vec \beta=(q-p)(\vec\beta·\vec\beta)\]由于对β的非零要求(否则就是H了),把β^2除过去,定义一个Γ
\[\Gamma(\alpha/\beta)=\frac{2\vec\alpha·\vec \beta}{\vec\beta·\vec\beta}=q-p\]也即在α为基础上利用β造升降链的下降深度-上升深度,并且由于范围许可,α-Γβ也是个根
将β当作自变量,最后半句话描述了根α诱导的作用在其他根上的反射,成为α对应的Weyl reflection。所有根给出的Weyl反射共同生成一个群,叫做Weyl群
正根的划分与Weyl腔一一对应,同个Weyl腔中的矢量给出了同个正根划分,进而给出了同个素根标注
Weyl群在Weyl腔构成的集合上的左作用是自由传递的
推论1:若α是根且kα也是根,则k=±1
注意这里的根是非零的。事实上0根对应了所有cartan中的生成元(简并)
证明:
\[\Gamma(k\alpha/\alpha)=2k;\Gamma(\alpha/k\alpha)=k/2\]上面都是整数,解得k=±2,±1,±1/2;而[Ea,Ea]=0,所以2a不是根;若a/2是根,则a不是根,矛盾。所以k=±1
推论2:两根夹角
\[cos^2(\alpha,\beta)=\frac{1}{4}(q-p)(q'-p')\]而(q-p),(q’-p’)均为整数,且cos平方属于[0,1],所以两根夹角的cos只可能取30°,45°,60°以及他们关于y轴的对称
任意李代数中的su(2)子代数
令
\[E^{\pm}=E_{\pm\alpha}/|\vec\alpha|\] \[E_3=\vec \alpha·\vec H/|\vec\alpha|^2\]则有对易关系
\[[E^+,E^-]=E_3~~~[E_3,E^\pm]=\pm E^\pm\]也即,每个根α都可以导出一组与su(2)同构的子代数
在下文中大量运用到的这个su(2)子代数大多作用基矢是伴随表示中的基矢(也可以理解为,伴随表示中的一个小结构)三个独立生成元对应三个独立基矢,这在同构意义下是su(2)的三维表示,也即j=1的表示;在此表示中,E3的特征值有且仅有-1,0,1
su(3)
在进入su(3)李代数之前先从SU(3)中解读出一些必要的信息
SU(3):三阶复方阵,满足$AA^\dagger=I,det(A)=1$,对其每个分量列限制条件
对角线上$\sum_j |a_{kj}|^2=1,k=1,2,3$,它提供了三个实限制
非对角线上$\sum_j a_{kj}a_{lj}^*=0,k\ne l$,他提供了3个复限制,6个实限制
最后,det=1提供了一个实限制,总独立分量个数为
\[18-3-6-1=8\]这下面顺便把一般SU、SO的自由度给出来
定理:SU(n)有n^2-1个独立元素
证明:SU(n)的幺正性等价于生成元厄米,det=1等价于生成元无迹
n*n的厄米阵拥有严格上三角区域的n(n-1)个实变量,以及对角线上n个实变量,最后减去一个无迹,最后得到n^2-1
定理:SO(n)有n(n-1)/2个独立元素
证明:还是和上面一样沿用厄米无迹so(n)生成元,但是由于SO(n)是实的,所以求导一定是实的,抽掉i之后生成元so(n)是纯虚的,纯虚厄米阵对角线上一定全0,只有对角线单侧区域是自由的,也即有n(n-1)/2个独立变量
找su2独立生成元的任务也即找8个独立的无迹3阶厄米阵,他们7个是泡利矩阵插0生成的,1个事编出来的
把泡利两个非对角阵插3次0,得到6个生成元
\[\lambda_1=\begin{pmatrix} 0&1&\\ 1&0&\\ &&0 \end{pmatrix}\lambda_4=\begin{pmatrix} 0&&1\\ &0&\\ 1&&0 \end{pmatrix}\lambda_6=\begin{pmatrix} 0&&\\ &0&1\\ &1&0 \end{pmatrix}\] \[\lambda_2=\begin{pmatrix} 0&-i&\\ i&0&\\ &&0 \end{pmatrix}\lambda_5=\begin{pmatrix} 0&&-i\\ &0&\\ i&&0 \end{pmatrix}\lambda_7=\begin{pmatrix} 0&&\\ &0&-i\\ &i&0 \end{pmatrix}\]把非对角插个尾巴,得到一个生成元
\[\lambda_3=\begin{pmatrix} 1&&\\ &-1&\\ &&0 \end{pmatrix}\]剩下一个是满秩对角,编出来的
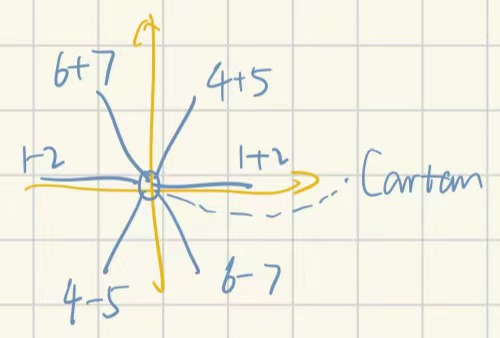
\[\lambda_8=\frac{1}{\sqrt{3}}\begin{pmatrix} 1&&\\ &1&\\ &&-2 \end{pmatrix}\]把上面这些λ÷2成为一组T,下面对T进行操作
一眼能看出两个对角T3、8组成cartan子代数,所以su3的rank是2
关于上升下降算符的组合,也就是把非对角同位置的一虚一实矩阵凑对就好
在这个规定下的su2上升下降算符使用$\frac{1}{\sqrt{2}}(J_1\pm iJ_2)$
下面给出每对升降符以及箭头后面对应的3号,8号生成元为顺序的根
\[\frac{1}{\sqrt{2}}(T_1\pm iT_2)\to\pm(1,0)\] \[\frac{1}{\sqrt{2}}(T_4\pm iT_5)\to\pm(\frac{1}{2},\frac{\sqrt{3}}{2})\] \[\frac{1}{\sqrt{2}}(T_6\pm iT_7)\to\pm(-\frac{1}{2},\frac{\sqrt{3}}{2})\]作出根矢量所在的平面图
dlc:更多李代数的根图
摘自参考5
原有矩阵对应基下的三个权矢量图,构成一个正三角形

dlc,但是和下面连贯,基本抄自参考3
1.r秩半单李代数有r个线性无关的根矢量
2.在保持cartan-killing度规不变的情况下,对cartan子代数生成元Hi进行线性重组,保持重组矩阵正交的时候,根α也在作正交变换;总存在一种正交重组,使得根全为实数(就算你放着不组合,自己内积自己也是个非退化的实数)
太棒啦,不需要在烦人的复空间研究根
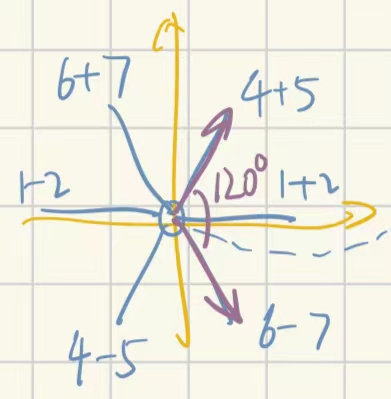
素根
意图是挑出所有根矢量中最大独立集,这个集合中的根就是素根
首先每个根都是正负成对出现,所以先记第一个非零分量为正数的根为正根;一个不能被其他正根的非负组合表出的正根即为素根
定理:素根的差不是根
证明:反证,素根a-素根b=根c,若c是正根,则a被表示为两个正根和;反之b被表出,均违背素根条件,证毕
定理:素根不可能成锐角
证明:沿用上面的Γ,由于素根差不是根,所以两个素根的下降深度为0,所以Γ(a/b)是非正的,把实数正分母乘过去他还是非正的,代表着内积非正,所以不可能成锐角,证毕。
因此素根之间的夹角只可能是90,120,135,150
定理:素根之间线性无关
反证:假设线性相关,则必有素根乘上各自的系数加起来为0;把系数中正负分离,记作矢量V
\[V:=\sum c_i\alpha^i=\sum d_j\beta^j\]其中,这两组矢量和都是素根的正线性组合,现在求V的模长
\[V·V=\sum_{ij}c_id_j\alpha^i·\beta^j\le0\]这与之前推出的自己内积自己非退化正定矛盾,原命题成立
用紫色标注出su3的两个素根
dynkin图:
用两个圈之间的连线数代表素根之间的夹角:90,120,135,150分别划线数为0,1,2,3;以su3两个夹角为120的素根为例,就是两个圈圈用一横连起来
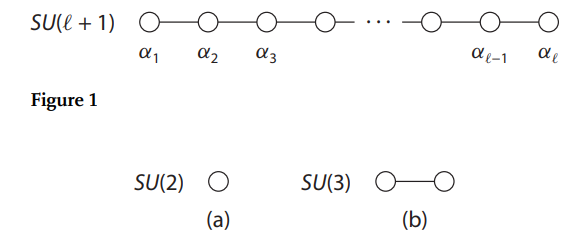
定理:同个李代数下素根至多有两种不同长度
所以在dynkin图中用空心点标注较长根,实心点标注较短根(AZee搞法);或者长指向短打个箭头
定理:李代数有直和分解$\Leftrightarrow$dynkin图不联通
证明:充分性显然,直和分解不同部分中的根构成的Γ必然为0(否则在一边进行上升下降时,另一部分受影响)
必要性:如果dynkin图断开,则来自不同部分的任意根正交,也即根链上升深度=下降深度;又因为素根差不是根,所以根链长度为1(他自己),所以某一部分内根生成的一套su(2)子代数与不同部分所生成的完全对易,李代数分解为两个理想的直和
定理:一个给定的dynkin图(与下文的cartan矩阵等价)可以在同构意义下唯一决定一个李代数
证明在参考3附录25,比较长就不抄了
Cartan矩阵
素根夹角与Γ的关系
\[\Gamma(\alpha/\beta)=\frac{2\vec\alpha·\vec \beta}{\vec\beta·\vec\beta}=q-p\]review:也即在α为基础上利用β造升降链的下降深度-上升深度
Cartan矩阵:一个rank阶的方阵(利用素根数恰好为rank的原理),i行j列的分量是第i与第j个根构成的Γ,即
\[A_{ij}=\Gamma(\alpha_i/\alpha_j)=\frac{2\vec a_i·\vec a_j}{|\vec\alpha_j|^2}\]α与β的夹角余弦写作
\[cos(\alpha,\beta)=\frac{1}{2}\sqrt{\Gamma(\alpha/\beta)\Gamma(\beta/\alpha)}\]当αβ均为素根时,他们构成的Γ只能取0,-1,-2,-3;记较长根为μ,有如下的关系表

dynkin图导出cartan矩阵:首先对每个圈圈编号,在表中查出角度对应的Γ值,填入相应的交叉位置;对角线上全填2
矩阵导出图:首先画出行(列)序号对应的圈圈,根据交叉对称位置的两个Γ判断角度和相对长度,进而确定点要不要涂黑以及要连多少条线
对单个su(2)子代数下降时对临近m的影响
现在有两个不同根α1,α2导出的su(2)子代数,以及一个共同本征矢|m,m’>,其中m是第一个子代数中E3的本征值,m’是第二个子代数中E3’本征值
现在尝试用α导出的第一个子代数中的下降算符对|m,m’>进行下降
\[E^-=E_{-\alpha_1}/|\alpha_1|\] \[E^-|m,m'>=|\alpha_1|^{-1}E_{-\alpha_1}|m,m'>\]然后用第二个子代数中的$E_3’$来检测第二个特征值是否发生变化
\[E_3'E^-|m,m'>=|\alpha_1|^{-1}|\alpha_2|^{-2}\sum_i\alpha_{2i}·H^iE_{-\alpha_1}|m,m'>\]将
\[[H^i,E_{-\alpha_1}]=-\alpha_{1i}E_{-\alpha_1},H^iE_{-\alpha_1}=[H^i,E_{-\alpha_1}]+E_{-\alpha_1}H^i=-\alpha_{1i}E_{-\alpha_1}+E_{-\alpha_1}H^i\]代入上式,得
\[E_3'E^-|m,m'>=|\alpha_1|^{-1}|\alpha_2|^{-2}\sum_i\alpha_{2i}·(-\alpha_{1i}E_{-\alpha_1}+E_{-\alpha_1}H^i)|m,m'>=(m'-\frac{\vec\alpha_1·\vec\alpha_2}{|\vec\alpha_2|^2})E^-|m,m'>\]也即,在第一个下降算符作用下,会使得第二个特征值也改变$-\frac{\vec\alpha_1·\vec\alpha_2}{|\vec\alpha_2|^2}=-\frac{1}{2}\Gamma(\alpha_1/\alpha_2)$;而素根的Γ非正,所以这个连带作用通常会将其他的m本征值上升(或者不改变,如果两根垂直)
所以我们给出了Cartan矩阵的(另一个)含义:对于第i个素根给出的su2子代数的下降算符E3,直接看第i个行矢量,他告诉我们E3作用后对全体子代数中m的影响的两倍
在下一节中通过在方框里写两倍权下降的方式,下降一次改变的数值恰好是cartan矩阵行矢量
最高权表示
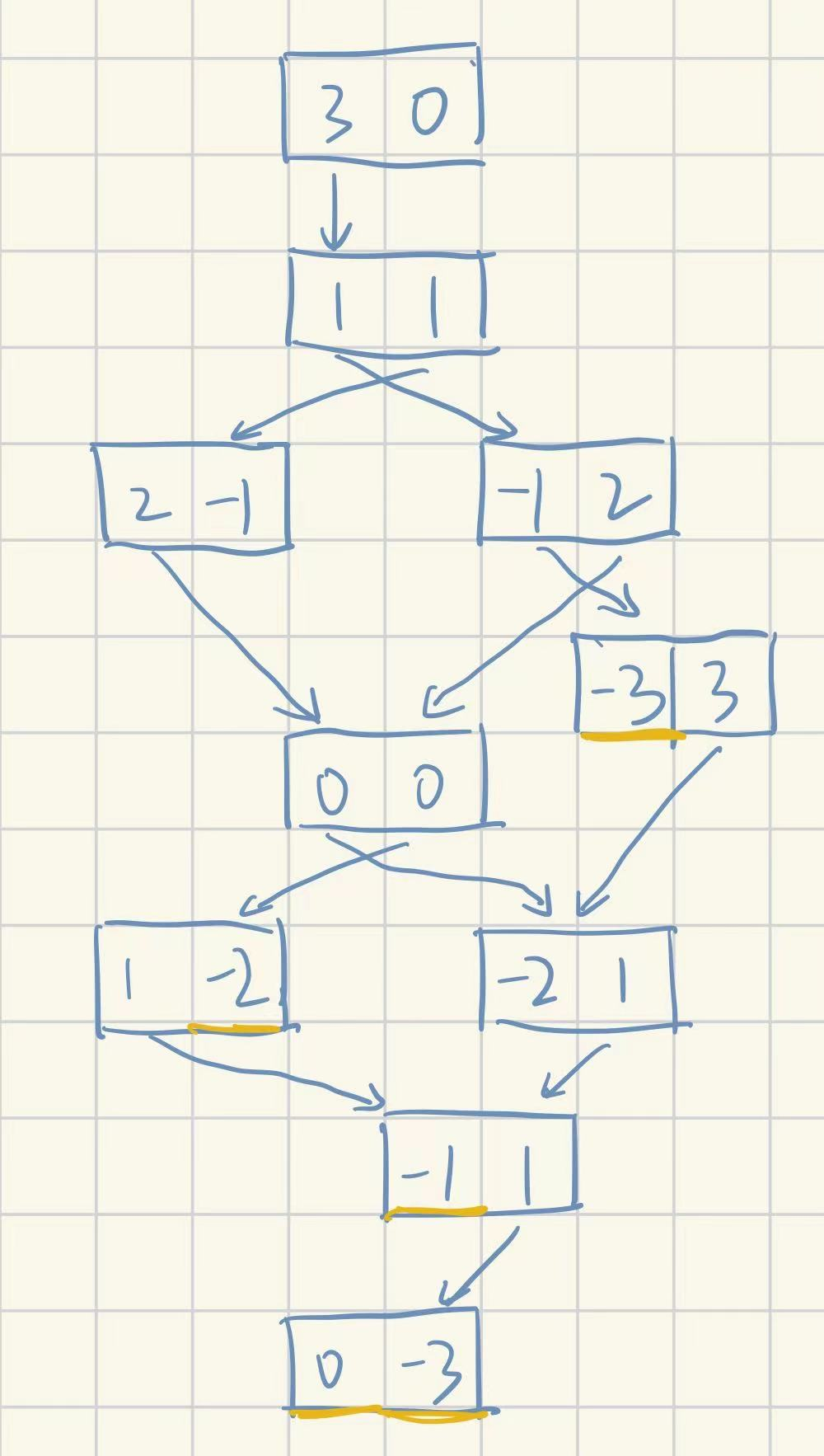
给你rank个数字标出的最高权,相当于对李代数中的相互耦合(?)在一起的su(2)每个都降到最低为止,下面以su(3)为例,他的cartan矩阵为
\[\begin{pmatrix} 2&-1\\ -1&2 \end{pmatrix}\]也就是说你下降2必然会让隔壁上升1
例如:左最高权(1/2,0);右最高权(0,1/2)(注意你写到格子里要乘2)
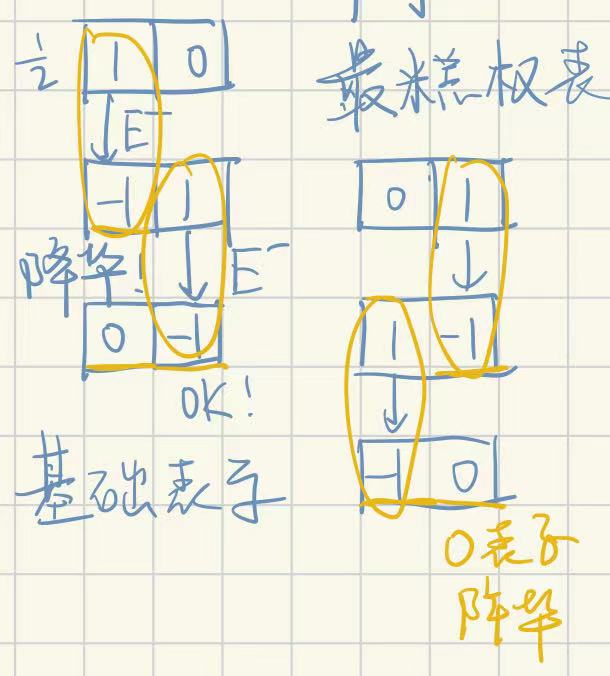
下降结束时用黄笔描了一下底;虽然这两个表示是共轭的,但是共轭不是相似变换,所以他们不是等价表示;然后表示的维度数格子数就好了,他们是三维表示(注意你下降的时候会开启隔壁一系列新的表示,你得把那些表示也下降到-j,直到你最后一条下降链把隔壁带成0,就不用下降了)
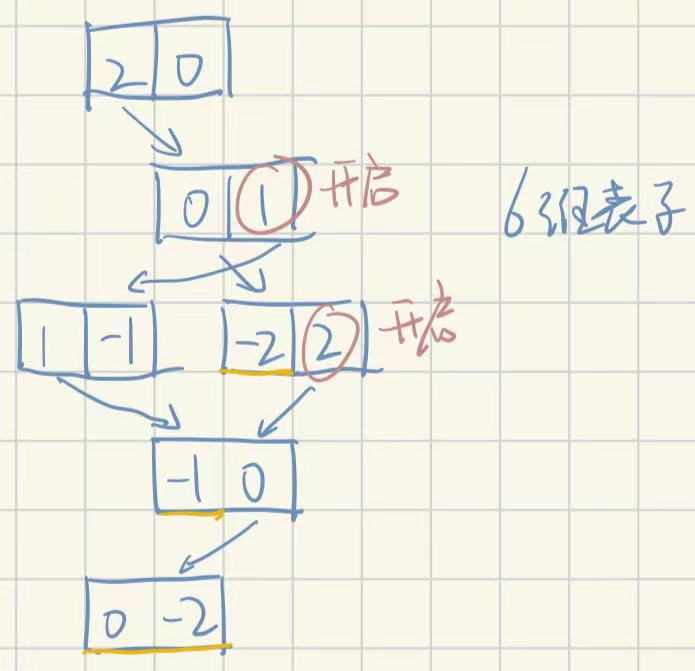
下面再看看(1,0)
下面看看双1/2表示
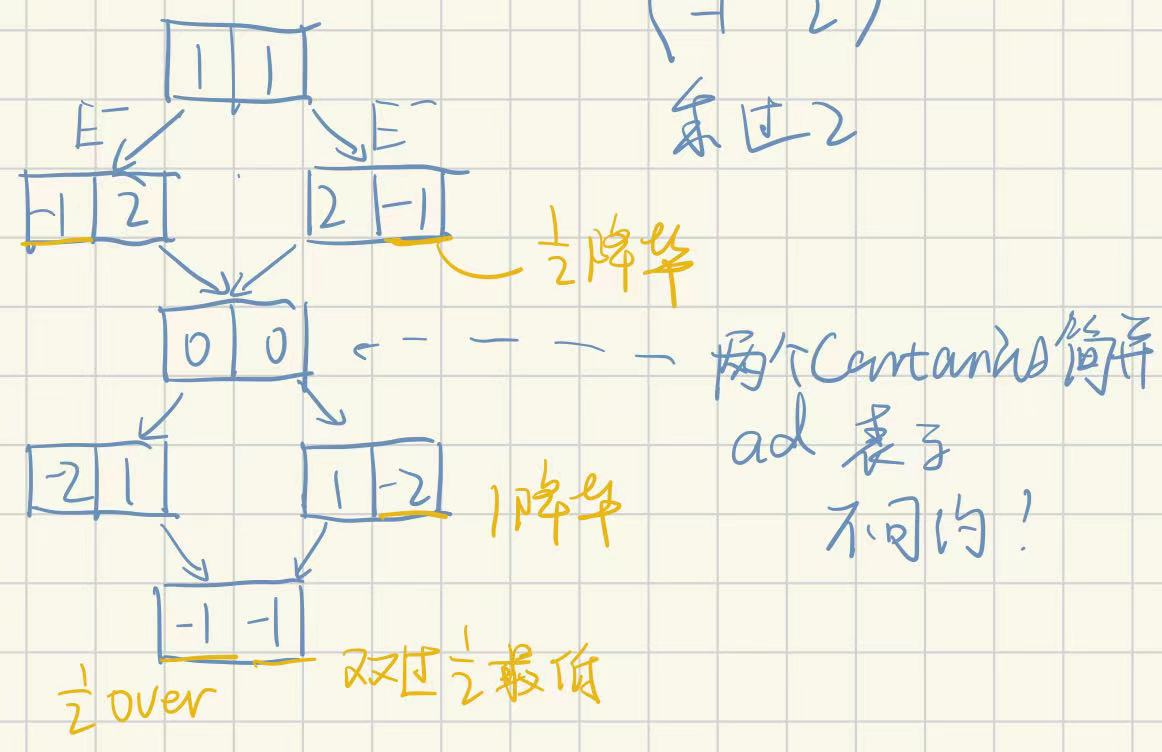
这玩意就是su3的伴随表示,这个随随便便的伴随表示很巧妙的是不可约的
还有个(3/2,0)表示
一个特殊的情况:SO(4)
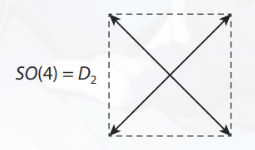
它仅有两组互相垂直的素根,在下降过程中不会相互影响,所以可以看出$so(4)\simeq su(2)\otimes su(2)’$
附录
将一些非常丑、暴力、与主线无关的证明放在这里。(绝对没人看)
附1.设实矩阵$D_k$表示从k层下降的作用矩阵,则其转置$D_k^T$表示从k+1层上升到k层的作用矩阵(因为你归一化系数上下是相等的)
\[D_k=\begin{pmatrix} c(j',j'-k)&&&\\ c(j,j)&c(j',j'-k+1)&&\\ &c(j,j-1)&\ddots&\\ &&&c(j',j')\\ &&&c(j,j-k) \end{pmatrix}\]可以看出一次下降上升的过程$D_k^TD_k$是一个实对称矩阵,而我们直和分解找到的新基矢正是每一个k导出的$D_k^TD_k$的特征矢空间;为了证明这个结论,使用归纳法
归纳法第一步:证明每一列J-作用链的首个向量是$D_k^TD_k$的特征矢。考虑一条一条下降的过程,当我们创造下降链首个向量时,此时空间已有dim-1个相互垂直的特征向量了,再造一个与先前所有向量均垂直的向量时,他一定也是对称矩阵$D_k^TD_k$的特征矢。
归纳法第二步:假设之前造出来的所有向量其对应$D_k^TD_k$的特征矢,考虑一次下降,证明本次下降会将k层的特征矢|k>打到k+1层的|k+1>,是$D_{k+1}^TD_{k+1}$特征矢
首先,若|k>是$D_k^TD_k$的特征矢,则$D_k\ket{k}=\ket{k+1}$是$D_kD_k^T$的特征矢;命题转化为证明$D_kD_k^T$与$D_{k+1}^TD_{k+1}$有同一套特征基,由引理1.1,即证$D_kD_k^T$与$D_{k+1}^TD_{k+1}$对易
为了方便(反正都是一回事),就不去注意这些矩阵的规格了,下面就是《臭搞计算的》环节
\[D_kD_k^T=\begin{pmatrix} c^2(j',j'-k)&c(j,j)c(j',j'-k)&&\\ c(j,j)c(j',j'-k)&c^2(j,j)+c^2(j',j'-k+1)&&\\ &c(j,j-1)c(j',j'-k+1)&\ddots&\\ &&&c^2(j,j-k)\\ \end{pmatrix}\]\[D_{k+1}^TD_{k+1}=\begin{pmatrix} c^2(j,j)+c^2(j',j'-k-1)&c(j,j)c(j',j'-k)&&\\ c(j,j)c(j',j'-k)&c^2(j,j-1)+c^2(j',j'-k)&&\\ &c(j,j-1)c(j',j'-k+1)&\ddots&\\ &&&c^2(j,j-k)+c^2(j',j')\\ \end{pmatrix}\]注:这是一个主对角线,附带上下两条次对角线的形式,下面的也类似
\[(D_kD_k^T)^i_i+(D_{k+1}^TD_{k+1})^{i+1}_{i+1}=(D_{k+1}^TD_{k+1})^i_i+(D_kD_k^T)^{i+1}_{i+1}\]注意到这两个矩阵的副对角线全部相等,所以他俩可交换等价于相邻对角线元交换和相等,也即下面这个式子
我们把它具体写出来
\[c^2(j,m)+c^2(j',m')+c^2(j,m)+c^2(j',m'-2)\\=c^2(j,m-1)+c^2(j',m'-1)+c^2(j,m+1)+c^2(j',m'-1)\] \[2m(m-1)+m'(m'-1)+(m'-2)(m'-3)=(m-2)(m-1)+2(m'-2)(m'-1)+m(m+1)\]可以验证上式是恒等式,故原命题得证,每一层生成出的向量均为下降上升矩阵的本征矢。
附2.-Open Problem-
这是我还没能解决的问题。对于实对称的,仅主对角和两条副对角有非零元素的矩阵
\[D_kD_k^T=\begin{pmatrix} c^2(j',j'-k)&c(j,j)c(j',j'-k)&&\\ c(j,j)c(j',j'-k)&c^2(j,j)+c^2(j',j'-k+1)&&\\ &c(j,j-1)c(j',j'-k+1)&\ddots&\\ &&&c^2(j,j-k)\\ \end{pmatrix}\]能否证明该矩阵的谱恰为${J(J+1)-M(M+1);M=j+j’-k,J=j+j’,j+j’-1,…}$?
这种没什么优点的矩阵想直接谱分解还是太难了。。。
未完待续
时时刻刻,物理启动!
参考
(0.?)乐乐、森林姐给的笔记;以及耐心听我讲{我脑子里冒出奇妙点子}的yqy、zbf超人学长
1.樱井纯《现代量子力学》
2.董无极《Group Theory in Physics》
3.马中骐《物理学中的群论》
4.《Lie Algebras in Particle Physics》
5.《Group theory in a nutshell for physicists》
原创文章转载请注明出处: 群论二