【同步更新】物理向群论:随手记
把有点意思的内容自己复现一遍,但是覆盖不了所有上课内容
警告:非常个人向,甚至接近于日记,有许多屁话和不严谨的地方
\[\require{physics}\]群的基本概念、性质
凯莱定理
每个群G同构于对称群$S_G$的一个子群
对应法则:取$g\in G$,左作用于G后得到G的一个置换$gG$,同时这个置换方式也是对称群$S_G$中的一个元素。由消去律可以验证这个(同构)映射是单射;再验证保运算,取G中元素a,b,打到SG中的a’,b’上,那么ab的作用效果正是a’b’,这是由群的结合律保证的;至于子群,封闭性由原群G保证了。
这告诉我们可以用置换的方式去理解群元
性质:在这种同构方式中,只要是含有不动点的置换必定是单位元,必定全部不动;并且所有对应过去的置换循环节长度唯一(对长度为n的循环节,反复作用n次即可归为不动;由上一条可知要么都动要么都不动,所以循环节长度只能出现一种)也就是说质数阶群对应的循环节长度只有1和它本身
共轭类
形式上很像矩阵相似
\[a\sim b\Leftrightarrow \exists g,s.t.a=gbg^{-1}\]阿贝尔群的每个元素自成共轭类
群中心:与所有元素均交换的群员组成的子群(一定是正规子群)
定理:共轭类中元素的循环结构必定相同(也即阶相同)
证明:先证明互换左右作用的单循环节保长度,也即
\[g=(b_1,b_2)(a_1,a_2,...,a_n)(b_1,b_2)\]保循环节长度n
1.若ai与bi两两不同(不相交),则含a的循环节与含b的循环节可交换,g=(a_1,a_2,…,a_n)保循环节长度
2.若b1b2中出现一个在a中,不妨设b1=ak,但b2不出现在a中,则
\[\begin{aligned} g & = (b_1,b_2)(a_1,a_2,...,a_k,...a_n)(b_1,b_2) \\ & = (a_k,b_2)(...,a_n,a_1,...,a_k)(a_k,b_2) \\ & = (a_k,b_2)(...,a_n,a_1,...,a_k,b_2) \\ & = (a_k,b_2)(a_k,b_2)(b_2,...,a_n,a_1,...) \\ & = (b_2,...,a_n,a_1,...) \\ \end{aligned}\]相当于用b2替换了原a循环节中的b1,长度不变
3.若b1b2全部出现在a中,则
\[\begin{aligned} g & = (b_1,b_2)(a_1,a_2,...,b_1,b_2,...a_n)(b_1,b_2) \\ & = (...,a_n,a_1,...b_2)(b_2,b_1) \\ & = (...,a_n,a_1,...b_2,b_1) \end{aligned}\]长度不变
又因为所有置换群中元素均可表示为若干对换的积,故任取$q\in S_n$,q可以表示为
\[q=(b_1,b_2)(c_1,c_2)...(h_1,h_2)\] \[q^{-1}=(h_1,h_2)...(c_1,c_2)(b_1,b_2)\]作用在(a_1,a_2,…,a_n)上,可得
\[(b_1,b_2)(c_1,c_2)...(h_1,h_2)(a_1,a_2,...,a_n)(h_1,h_2)...(c_1,c_2)(b_1,b_2)\]多次利用结合律和上面已经证明的结论,可得上式结果也是长为n的循环节
至于对多个循环节的作用,可以这样添元素
\[q(a_1,...,a_n)(b_1,...,b_n)q^{-1}=[q(a_1,...,a_n)q^{-1}][q(b_1,...,b_n)q^{-1}]\]最后仍然是保循环结构的
至此,我们证明了共轭类中元素的循环结构必定相同。
加一点我个人对共轭类的啰嗦理解:从某种角度来看,共轭类的元素其实是本质一样的,但是群中的不对易性使得他俩看起来外观长得不一样(或者说穿了不一样的衣服),所以说完全对易的阿贝尔群就没人把本质一样的东西拉开,你本质一样,外观也就全部一致了;
你看两个互相共轭的元素,之间好像就差一个同声传译,一个负责翻译的,翻译了给另外一个人处理,处理完了再翻译回去,效果是一样的(我也不知道写这么多显然的屁话有什么用,大概是希望如果我有几年不接触这些概念之后,不要对着这个共轭类概念发愣吧)
对Sn共轭类的刻画
对于任意一个群,利用凯莱定理打到Sn的子群上并划分共轭类,则有:共轭类中的循环结构必定相同,但循环结构相同的元素不一定在同一共轭类上(如克莱因群除单位元以外均是2:2循环结构,但是他是阿贝尔群所以每个元素自成一个共轭类)
感性地理解:这主要是因为gag-1左手右手的g不在子群中,而是在Sn大群中
但是对于整个Sn群,有更强的结论:循环结构相同<=>同一共轭类
上节给出了必要性证明,下面仅需证充分性。这需要对gag-1这种东西有更深刻的把握,先来证明这个结论
设$g,a\in S_n;~~g:i\mapsto g(i)$,a用循环写作
\[a:(i,j,...,m)(k,..,l)\]则$gag^{-1}$用循环写作
\[gag^{-1}:(g(i),g(j),...,g(m))(g(k),..,g(l))\]就像线性代数中的“以g为基下的变换a”
证明比发现要简单。我们观察一下gag-1把g(i)打到哪里:
\[g(i)\stackrel{g^{-1}}{\rightarrow}i\stackrel{a}{\rightarrow}j\stackrel{g}{\rightarrow}g(j)\]该引理得证
由此,假设有两个结构一样的置换,只需建立映射q把循环节内容一个个映过去(类似上文的i映到gi,j映到gj等等);由循环节中单字至多出现一次可知q单射,则必定能在Sn中找到(不唯一)满足条件的q。所以两个结构一样的置换必在同一共轭类中
共轭类中元素个数
已确定循环结构为:长度为i的节有ai个。例(x)(x)(xx)(xxx)所对应的a1=2,a2=1,a3=1,且1+1+2+3是总元素个数(非省略计法),那么Sn中(回到ai表示)的元素个数有
\[\frac{n!}{\Pi i^{a_i}a_i!}\]分母中的i^ai代表每一个循环节有其长度种等价写法,共有ai个这样的循环节;ai!代表无需考虑等长循环节之间顺序
群表示论
a?第二周就开始表示论了吗 我是不是少看了几集.jpg
群的表示就是把群元hom到线性变换上;同构就是忠实表示,如果ker非平凡那就是简并表示
还有函数表示,设群元对应的线性变换是a,那么对于一个给定的关于坐标的线性函数f(x),a作用在f上相当于f(ax)把a拿出来变成f’(x)
原群的简并表示可以诱导一个特定商群的忠实表示(模ker呗);商群(不平凡)的表示诱导原群的简并表示(用pi映射)。
概念-等价表示:表示之间的等价性指的是在两个表示之间存在一组固定的基,通过换基将同一群元的两种表示相等起来;那么根据这个等价关系同样可以将表示之间划分为不同的等价类,等价类所构成的集合与这个商群一一对应:
\[Hom(G;GL(m;\mathbb{C}))/GL(m;\mathbb{C})\]为了完整性插一句显然的话:幺正表示必然是定义在内积空间中的
| 定理1:可约的幺正表示必可分解:即证不变子空间的补空间不变,只看(正交)基。取不变子空间的基ei,补空间基ej,则<ei | ej>=0再用上幺正条件<ei | UU+ | ej>=0即U作用后仍是正交补,所以补空间也是不变子空间 |
定理2:有限群的表示必等价于某个幺正表示。(也就是要找换基S使得SDS-1全部幺正)
先开始我觉得还得要求原表示的所有矩阵ker的交为0,,后来发现单位元打到矩阵上一定是单位阵,ker=0!
构造新引理:注意到(平均内积)在群作用下不变
\[(v,w)=\sum_{g\in G}<D(g)v|D(g)w>\]也就是定义一个新内积(内积合法性易验证),它等于群作用后所有内积和。对这个内积施以一个群变换,可以由重排引理验证他是不变的。
\[(D(g')v,D(g')w)=\sum_{g\in G}<D(g')D(g)v|D(g')D(g)w>=\sum_{g\in G}<D(g)v|D(g)w>=(v,w)\]幺正变换=保内积,这和要证明的东西息息相关
| 上面定义了一个新内积(v,w),那么是否存在线性变换S,使得(v,w)=<Sv | Sw>呢? |
由内积四条可以看出,向量(已知基上展开系数)内积完全取决于基之间的内积情况,现在把S想作一个nxn的待定矩阵。取一对基(n+nC2=n(n+1)/2种取法),用上面的定义式计算内积大小,由此可以得到n(n+1)/2个限制方程,此时有n^2个待解元,必然存在这样的S,这就是要找的新基,等价的幺正变换写作
\[U(g)=SD(g)S^{-1}\]验证原内积在U下不变:
\[\begin{aligned} & < Uv|Uw> \\ & =< SDS^{-1}v|SDS^{-1}w> \\ & = \sum_{g\in G}< D_gDS^{-1}v|D_gDS^{-1}w> \\ & = \sum_{g\in G}<D_gS^{-1}v|D_gS^{-1}w> \\ & = (S^{-1}v,S^{-1}w) \\ & = <v|w> \end{aligned}\]也就是说,在等价的意义下,所有有限群表示都是幺正、可约=可分解的,所以下面的有限群内容会时不时默认表示幺正、可约可分解混用。
舒尔引理
1.U(G)是G的在线性空间V上的不可约表示,A是V上的算符(相当于是个矩阵/线性映射,和U(g)同级,但不要求在群内),如果对任意的g有
\[AU(g)=U(g)A\]A可以和群的表示交换,有点像中心但是不要求群内
那么一定有
\[A=\lambda I\]证明:在C上,A必定有一个特征λ及对应的特征空间$V_\lambda$,取$\forall x \in V_\lambda,g\in G$,则
\[U(g)Ax=AU(g)x=\lambda U(g)x\]也即,$V_\lambda$是U(g)的不变子空间;由于不可约表示没有非平庸的不变子空间,再加上A的特征空间存在性,所以$V_\lambda=V\Rightarrow A=\lambda I$
由此可以迅速得到一个结论:交换群的不可约表示是一维的
2.对群G,U是V上不可约表示,U’是V’上不可约表示,这两个表示不等价;有映射A:V’->V.使得
\[AU'(g)=U(g)A~~,\forall g \in G\]那么要么这两个表示是完全相同的(进入舒尔引理1),要么A=0
证明:还是和上面一样,构造一个平庸的不可约表示的不变子空间,将U作用在imA上:(不严谨但是爽)
\[UimA=UAx=AU'x\in imA\]也即imA是U的不变子空间,要么imA=0,A=0;要么imA=V
对称的,再用AU’作用在kerA上
\[AU'kerA=UAkerA=0\Rightarrow U'kerA\in kerA\]要么kerA=V’,A=0;要么kerA=0
当kerA=0且imA=V时,A建立了V’与V之间的同构,此时U与U’有这样的关系
\[U(G)=AU'(G)A^{-1}\]也即两表示等价,表示的像所处的线性空间同构
用更精炼的语言再叙述一遍
有两个表示,v in End(V),w in End(W),记在Hom(V,W)中满足fv=wf的f组成线性子空间$Hom^G(V,W)$,那么要么v和w等价,$dim(Hom^G(V,W))=1$,要么表示不等价,$dim(Hom^G(V,W))=0$
不止在复数域C上的表示的舒尔引理
V是有限群G在域k上的的不可约表示,那么能与所有表示交换的$End^G(V)$是k上的有限维除代数(除环+k代数)
解释:不限定交换性的算子End(V)自然构成k代数(矩阵一般都是代数的,毕竟线性空间配备乘法,你懂的),加上交换性限定后升级为除代数(也即所有乘法有逆,在线性结构上表示为$ker(End^G(V))=0$)
证明:重点在于证明乘法可逆性
对于任何与群作用对易的算符$\phi\in End^G(V)$,必然有两个不变子空间kerφ和imφ,而不可约表示的不变子空间平凡,故要么φ可逆要么φ=0,又因为有限群表示必是有限的,所以$End^G(V)$是k上的有限维除代数
回到C版舒尔借助这个:C上的有限维除代数是C自己
证明:运用到C[x]上的代数基本定理
在有限维代数中,任取一元a,不断生成{a,a^2,…}直到这组向量线性相关,也即,存在多项式$P\in C[x]$,使得P(a)=0
另一方面,对多项式P进行因式分解,$P(x)=\Pi(x-x_i),x_i\in C$,代入a得$P(a)=\Pi(a-x_i)=0$,除环内乘积为0则有一项为0,$\exists i,a=x_i\in C$,故该代数就是C自己。
正交归一性定理
我觉得这节相当的数物!很有完备函数系下(展开)的感觉~
注:本节上下标混用,但是对于矩阵,上标代表行,下标代表列
正交归一:在一个大小为$n_G$的群上,对于两个不可约表示$U_\nu$和$U_\mu$,表示的维度记为$n_\nu$和$n_\mu$;对于一个表示矩阵$D_\mu(g)$,其分量写作$D_\mu(g)^i_j$的形式
那么现在固定{表示、矩阵分量位置ij}对于“群员遍历”产生的分量 组成的矢量:
\[\vec v_\mu(i,j)=(D_\mu(g_1)^i_j,D_\mu(g_2)^i_j,...,D_\mu(g_{n_G})^i_j)\]再把长度稍微改改(为了下面的“归一”),乘根号下表示维度除群规格
\[\boxed{\vec x_\mu(i,j)=\sqrt{\frac{n_\mu}{n_G}}(D_\mu(g_1)^i_j,D_\mu(g_2)^i_j,...,D_\mu(g_{n_G})^i_j)}\]变换$\vec x_\mu(i,j)$中的参数ij,一共可以产生$n_\mu^2$个矢量,这些矢量系是正交归一的,也即,当且仅当i=k,j=l时,有$\vec x_\mu(i,j)·\vec x_\mu(k,l)=1$,其他情况下内积为0
品味一下,想想正交函数系sinax,或者正交归一函数系球谐函数。。
用表达式写出来也即
\[\frac{n_\mu}{n_G}\sum_gD^\dagger_\mu(g)^k_iD^\mu(g)^j_l=\delta_i^j\delta_l^k\]这个式子可以进一步推广到表示之间的正交关系(我们将在证明中看出舒尔引理如何支撑这个结论),引入同样是不可约的表示$\nu$,得
\[\frac{n_\mu}{n_G}\sum_gD^\dagger_\mu(g)^k_iD^\nu(g)^j_l=\delta_\mu^\nu\delta_i^j\delta_l^k\]也就是说,不同表示之间的矢量x必定正交,等式为0
证明:先将上式左侧的分量形式改写成矩阵相乘形式,中间插两个δ
\[\sum_gD^\dagger_\mu(g)^k_iD^\nu(g)^j_l=\sum_{g,n,m}D^\dagger_\mu(g)^k_n\delta^n_i\delta ^j_mD^\nu(g)^m_l\]设$A^n_i=\delta^n_i;B^j_m=\delta^j_m$,其中A、B是矩阵,则AB可以视作一个仅有i行j列有元素1的矩阵,例如(i=2,j=3)
\[AB=\begin{pmatrix} 0&0&0\\ 0&0&1\\ 0&0&0 \end{pmatrix}\]继续将分量形式合并为矩阵相乘,注意到仅有k(行)l(列)是非求和变量,也即整体的行列标是kl
\[\sum_{g,n,m}D^\dagger_\mu(g)^k_n\delta^n_i\delta ^j_mD^\nu(g)^m_l\to\sum_g D_\mu^\dagger(g)ABD^\nu(g)\]证第一个克罗内克符号
这里要用到舒尔引理2,欲构造形式
\[D_\mu^{-1}(p)MD_\nu(p)=M~~,\forall p\in G~~(*)\]那就令$M=\sum_g D_\mu^\dagger(g)ABD^\nu(g)$,算算LHS试试(下面用到了逆=共轭转置)
\[LHS=\sum_g D_\mu^{-1}(p)D^\dagger_\mu(g)ABD^\nu(g)D_\nu(p)=\sum_g D^\dagger_\mu(gp)ABD^\nu(gp)\]由重排引理得上式
\[LHS=\sum_g D^\dagger_\mu(g)ABD^\nu(g)=M\]*式成立,所以我们可以由舒尔引理得,若$\nu!=\mu$,则M=0,若$\nu=\mu$,则$M=\lambda I$
\[\sum_g D^\dagger_\mu(g)ABD^\mu(g)=\lambda I\]欲求λ,则两边取trace,左侧
\[tr(\sum_g D^\dagger_\mu(g)ABD^\mu(g))=\sum_g tr[(D^\dagger_\mu(g)D^\mu(g))(AB)]\]其中,$D^\dagger_\mu(g)D^\mu(g)=I$,故$(D^\dagger_\mu(g)D^\mu(g))(AB)=AB$
若$i\neq j$,则AB主对角线上全为0,tr(AB)=0,λ=0
若$i=j$,则AB主对角线上有一个1,tr(AB)=1,此时
\[tr(\sum_g D^\dagger_\mu(g)ABD^\mu(g))=n_G=tr(\lambda I)=\lambda n_\mu\]综上,
\[\lambda=\frac{n_G}{n_\mu}\delta^j_i\]回代到原式,即
\[\sum_g D^\dagger_\mu(g)ABD^\mu(g)=\frac{n_G}{n_\mu}\delta^j_i I\]上式的两侧行列分量为kl,写作分量形式即
\[\sum_gD^\dagger_\mu(g)^k_iD^\mu(g)^j_l=\sum_{g,n,m}D^\dagger_\mu(g)^k_n\delta^n_i\delta ^j_mD^\mu(g)^m_l=\frac{n_G}{n_\mu}\delta^j_i \delta^k_l\]故
\[\frac{n_\mu}{n_G}\sum_gD^\dagger_\mu(g)^k_iD^\nu(g)^j_l=\delta^\nu_\mu \delta^j_i \delta^k_l\]
推论:不可约有限群表示的维数平方和不超过群大小
\[\sum_{\mu}n_\mu^2\leq n_G\]通俗的口头证明:对于每个不可约表示$\mu$(想成$n_\mu\times n_\mu$的矩阵),一共有$n_\mu^2$个矩阵分量,而每个分量ij都可以生成正交归一的$\vec x_\mu(i,j)$(忘记了就往上看有框的公式),并且每个不同表示间也是正交的,也就是说在$\vec x$所在的空间中有了$\sum_{\mu}n_\mu^2$个独立的矢量;而这个线性空间是$n_G$维的,由于线性空间中独立矢量数必小于等于空间维度,所以有$\sum_{\mu}n_\mu^2\leq n_G$
先对特征标进行一个小小的recall:表示中的矩阵,可能存在两两之间的矩阵相似关系(SAS-1=B),依据相似关系划分等价类(也即群中的共轭类),我们又知道trace是相似不变量,所以就用tr来刻画每个共轭类,记作$\chi^\mu_i$(表示$\mu$中共轭类i的矩阵迹)
上面中我们通过群元g作为分量生成了带框的那个向量x,现在用特征标替换{群元矩阵上的某个分量}生成y向量
\[\boxed{\vec y(\mu)=(\sqrt{\frac{n_1}{n_G}}\chi^\mu_1,\sqrt{\frac{n_2}{n_G}}\chi^\mu_2,...,\sqrt{\frac{n_i}{n_G}}\chi^\mu_n)}\]有多少个表示,就有多少个y向量;这组向量在不可约表示的前提下同样具有很好的正交归一性
\[\sum_i\frac{n_i}{n_G}{\chi_\mu^\dagger}^i\chi_i^\nu=\delta_\mu^\nu\]为证明特征标的正交归一性定理,取群元正交归一定理的特殊情况后取迹,这是原表述
\[\frac{n_\mu}{n_G}\sum_gD^\dagger_\mu(g)^k_iD^\nu(g)^j_l=\delta_\mu^\nu\delta_i^j\delta_l^k\]固定i=j(他们怎么样并不是这次关心的),并将kl看作矩阵分量指标,看作矩阵形式,左侧恰好是两个矩阵点乘
\[\frac{n_\mu}{n_G}\sum_gD^\dagger_\mu(g)D^\nu(g)=\delta_\mu^\nu I\]再求trace
\[\frac{n_\mu}{n_G}\sum_gtr(D^\dagger_\mu(g))tr(D^\nu(g))=\delta_\mu^\nu tr(I)\] \[\frac{n_\mu}{n_G}\sum_in_i\chi^{\dagger i}_\mu \chi^\nu_i=\delta_\mu^\nu n_\mu\]特征标正交归一性得证
任意表示的分解
任给群G的在V上的一个表示U,都可以在等价意义下分解为一些不可约表示的直和,这仅仅来源于线性空间的本性(之类的东西);对于这个线性空间V,找到每个群意义下的不变子空间,进行直和分解
\[V=\bigoplus_{不变}W\]对于表示而言
\[U=\bigoplus_{\lambda}\alpha_\lambda U^\lambda\]其中,右侧这些$U^\lambda$是G的不等价不可约表示,$\alpha_\lambda$表示出现的次数。欲求这个次数,对上式左右取迹
\[\chi^i=\sum_\lambda \alpha_\lambda\chi^i_\lambda\]利用这个等式构造框框向量y
\[\vec y =\begin{pmatrix} \sqrt{\frac{n_1}{n_G}}\chi^1\\ \sqrt{\frac{n_2}{n_G}}\chi^2\\ ...\\ \sqrt{\frac{n_i}{n_G}}\chi^i\\ \end{pmatrix}=\sum_\lambda \alpha_\lambda \begin{pmatrix} \sqrt{\frac{n_1}{n_G}}\chi^1_\lambda\\ \sqrt{\frac{n_2}{n_G}}\chi^2_\lambda\\ ...\\ \sqrt{\frac{n_i}{n_G}}\chi^i_\lambda\\ \end{pmatrix}\]等式同时对不可约表示形成的$\vec y(\mu)$做内积,由正交归一性得
\[<y|y(\mu)>=\alpha_\mu\]所以展开系数可以用内积的方式求得(这种模式大家应该都玩烂了)
推论:表示U不可约<=>$\norm{\vec y(U)}_2=1$
证:$\norm{\vec y(U)}_2$实际上是一些整数平方和的形式,若值为1则仅可能是一项为1,其他项均为0
实例:“正则表示”(regular representation)
设群G内的运算律为gi·gj=gk;将每个群元看作线性空间上V的基矢,定义V上的线性映射U(gi),满足
\[U(g_i)|g_j>=|g_k>\]则称该表示U为正则表示。这个线性映射刻画的是gi对群元的置换作用,举个例子,三元群的群元(123)的矩阵表示写作
\[\begin{pmatrix} 0&0&1\\ 1&0&0\\ 0&1&0 \end{pmatrix}\]单位元的表示一定是单位阵,非单位元的表示矩阵必定1)对角线为0 2)每行、列有且仅有一个1(这些性质都很好用重排引理证明)
正则表示对应的特征标框框向量写作
\[\vec y=(\sqrt{n_G},0,...,0)\]从模长可以看出是可约表示,下面通过求内积的方式来计算不可约表示$\mu$出现的次数
\[\alpha_\mu=<y|y_\mu>=\sqrt{n_G}·\sqrt{\frac{1}{n_G}}·n_\mu=n_\mu\]也即,不可约表示的出现次数恰为表示维数;单位元的正则表示$I_{n_G}$同样可以由这些不可约表示展开,用特征标写作
\[n_G=\sum_\mu n_\mu^2\]意思是说,所有不可约表示维度的平方和恰为群的阶数。谈笑间看似在玩正则表示的同时,得出了这个很有用的结论,在下面也会经常用到
完备性定理
完备性定理:
什么时候一组向量被称作“完备”呢?当然是这组向量能作为基底来描述整个空间中的任意向量,或者说span张成全空间V。当探讨一组正交归一向量{ei}的完备性时,可以直接说$\sum_i e_i\otimes e_i$是HomV上的单位算符,用狄拉克符号写作
\[\sum_i|i><i|=I\]下面给不太熟悉的读者提供更具体的矩阵观点。拿出一个正交归一中的基矢e1
\[\vec e_1 =\begin{pmatrix} 1\\ 0\\ ...\\ 0 \end{pmatrix}\]自张量积后,可以用矩阵写作(我不知道这里能不能写等号,至少是同构号吧)
\[\vec e_1 \otimes \vec e_1=\begin{pmatrix} 1\\ 0\\ ...\\ 0 \end{pmatrix}\begin{pmatrix} 1&0&...&0\\ \end{pmatrix} =\begin{pmatrix} 1&0&...&0\\ 0&0&&\\ \vdots &&\ddots&\\ 0&&&0\\ \end{pmatrix}\]那么
\[\vec e_1 \otimes \vec e_1+\vec e_2 \otimes \vec e_2=\begin{pmatrix} 1&0&...&0\\ 0&0&&\\ \vdots &&\ddots&\\ 0&&&0\\ \end{pmatrix}+\begin{pmatrix} 0&0&...&0\\ 0&1&&\\ \vdots &&\ddots&\\ 0&&&0\\ \end{pmatrix}= \begin{pmatrix} 1&0&...&0\\ 0&1&&\\ \vdots &&\ddots&\\ 0&&&0\\ \end{pmatrix}\]如果{$e_i$}能张成全空间,则
\[\sum_i e_i\otimes e_i=I\]对于非基的一组正交归一且完备矢量{xi},一定存在正交变换A,使得
\[A|e_i>=|x_i>\]故有
\[\sum_i x_i\otimes x_i=\sum_{i全} Ae_i\times e_i^TA^T=A(\sum_{i全} e_i\times e_i^T)A^T=AIA^T=I\]我们刚刚验证了正交归一完备->和为I,下面要反推正交归一和为I->完备
利用秩不等式rank(A+B)<=rank(A)+rank(B)
观察$\sum_i x_i\otimes x_i=I$,左侧每一项求和量的秩都是1,右侧的秩是dimV,也就是说i的个数必须>=dimV;又因为V中正交归一的矢量组最多有dimV个矢量,所以i的数目为dimV,又因为正交性,故spanxi=V完备
至此,和为I的条件与心中的完备性很好的结合起来了
上面都是前戏,现在隆重介绍群表示中的完备性定理
\[\sum_{\mu,l,k}\frac{n_\mu}{n_G}D^\mu(g)^l_kD^\dagger_\mu(g')^k_l=\delta_{gg'}~~(*)\]先讲讲为什么叫“完备性”;拿出我们的框框向量
\[\boxed{\vec x_\mu(i,j)=\sqrt{\frac{n_\mu}{n_G}}(D_\mu(g_1)^i_j,D_\mu(g_2)^i_j,...,D_\mu(g_{n_G})^i_j)}\]把*式中的g看成分量指标,对这个式子不用分量表示而是用矩阵表示,也即
\[\sum_{\mu,l,k}\frac{n_\mu}{n_G}{D^\mu}^l_k{D^\dagger_\mu}^k_l=I\] \[\sum_{\mu,l,k}\vec x_\mu(l,k)\vec x_\mu^\dagger(k,l)=I\]这恰好与$\sum_i\ketbra{i}=I$具有一致的形式,也就是说不可约群表示这组$\vec x$不仅相互之间正交归一,还能张成全空间V。
证明:注意到正交归一的矢量一共有$\sum_{\mu}n_\mu^2$个,而他们所在的空间维度为$n_G$,结合在表示分解那一节中得到的结论$\sum_{\mu}n_\mu^2= n_G$,完备性得证。
特征标完备性定理
\[\frac{n_i}{n_G}\sum_\mu\chi_i^\mu{\chi_\mu^\dagger}^j=\delta_i^j\]证明:
关于特征标的小引理:
\[\sum_{h\in class}U^\mu(h)=\frac{n_i}{n_\mu}\chi^\mu_iI\]左侧是对共轭类i中所有群元的表示求和,右侧的ni代表共轭类i中的元素个数
证明:看见右边有I,那就还是往舒尔靠,把LHS左右夹住试试
\[U^\mu(g)(\sum_hU^\mu(h))U^{\mu-1}(g)=\sum_hU^\mu(ghg^{-1})\]由(共轭类中的)重排引理得,上式仍然为$\sum_{h\in class}U^\mu(h)$,故
\[\sum_{h\in class}U^\mu(h)=\lambda_i^\mu I\]老套路求trace
\[tr(\sum_{h\in class}U^\mu(h))=n_i\chi^\mu_i\] \[tr(\lambda_i^\mu I)=\lambda_i^\mu n_\mu\]可得
\[\lambda_i^\mu=\frac{n_i}{n_\mu}\chi^\mu_i\]使用到矩阵元的完备性定理
用到矩阵元的完备性定理
\[\sum_{\mu,l,k}\frac{n_\mu}{n_G}D^\mu(g)^l_kD^\dagger_\mu(g')^k_l=\delta_{gg'}\]注意到这个等式所拥有的实际变量(与求和哑变量相对)是g和g’;并且gg’不同的时候RHS=0;现在关心gg’在同一共轭类i中的情况
在共轭类i中取gg’的值,一共可以造出ni^2个这样的等式,其中有ni个式子RHS=1,其余均为0;现在把这些式子全部求和
\[\sum_{\mu,l,k}\frac{n_\mu}{n_G}(\sum_{g\in class}D^\mu(g))^l_k(\sum_{g'\in class}D^\dagger_\mu(g'))^k_l=n_i\]将小引理代入LHS
\[\sum_{\mu,l,k}\frac{n_\mu}{n_G}(\frac{n_i}{n_\mu}\chi^\mu_iI)^l_k(\frac{n_i}{n_\mu}\chi^{\dagger\mu}_iI)^k_l=n_i\] \[\sum_{\mu}\frac{n_\mu}{n_G}\frac{n_i^2}{n_\mu^2}\chi^\mu_i\chi^{\dagger\mu}_i=n_i\] \[\frac{n_i}{n_G}\sum_\mu\chi_i^\mu{\chi_\mu^\dagger}^i=1\]而当求和共轭类不同的时候,重复上面操作,左边形式不变(仅把其中一个i更改),右边为0,结合在一起可得
\[\frac{n_i}{n_G}\sum_\mu\chi_i^\mu{\chi_\mu^\dagger}^j=\delta_i^j\]这节看到这里应该隐隐感觉到,正交归一和完备有种“对偶”或者“转置”的关系,一个纵向刻画,一个横向刻画。。。
本章脉络梳理:

特征标表
有了特征标的完备性定理后,可知不可约表示数=群G中的共轭类数,所以我们可以以共轭类、表示划分两个坐标轴,做成一张方表,表中填特征标
例如只有两个元素的C2群,其特征标表为
| $C_2$ | e | a |
|---|---|---|
| $U_1$ | 1 | 1 |
| $U_2$ | 1 | -1 |
C2所有不可约表示均1维(阿贝尔),所以表示=特征标。第一排无脑填1,因为每个群都有恒1的平庸表示。第二排的表示1和-1也很好想出来
此外,在填不出来的情况下,可以用待定系数,代入正交归一定理、完备性定理、$\sum n_\mu^2=n_G$来解出,例如S3的特征标表
规定共轭类1、2、3分别代表e、循环节长度为2、循环节长度为3
| $S_3$ | 1 | 2 | 3 |
|---|---|---|---|
| $U_1$ | 1 | 1 | 1 |
| $U_2$ | 1 | -1 | 1 |
| $U_3$ | 2 | 0 | -1 |
填表小寄巧
1.先填右边、上边:上边一排永远是1,右边一列代表着表示维度
2.是否阿贝尔:阿贝尔群则不可约表示全部1维,特征标和表示相等
3.(纵向)完备性:由于归一化系数$\sqrt{\frac{n_i}{n_G}}$中的ni在列内保持一致,而横着看不一定相等的特性,所以如果情况不够简单尽量避免用正交归一性,而是用完备性:一列竖着的平方和乘$\frac{n_i}{n_G}$=1
4.$\sum n_\mu^2=n_G$这些都是整数的运算,做起来比较方便,只剩几个表示待求时可以快速判断表示维度
5.找不可约表示的重点在于同态关系,所以可以从商群的不可约表示入手,再还原到原群中
直积表示
这里的直积不同于直和;直和就像是把两张不同的纸左边与右边贴起来,成为一张大大的平平的纸;直积(张量积)就像先量一下一张A纸的边长,然后狂暴搞一堆摞起来的B纸,使得摞的高度达到之前量的那个边长
直积表示的出现有着直接的物理动机:(没学过量力,听了个响)大意就是知道两个粒子的态,直积一下就成了他们整体的态(大概是这样?)
设有在基为{ui}的线性空间U上的表示拥有矩阵形式A,和{vi},V,B;那么直积表示所在空间W拥有基{wkj}=uk x vj,维度是dimUxdimV
令k表示有序数对(i,j),则直积表示的矩阵形式写作$D^{k’}_k=A^{i’}_iB^{j’}_j$,保群同态易验证
直积表示的特征标=小表示特征标的积
CG系数(Clebsch-Gordan coefficient)
也就是求直积表示拥有的自然基(uk x vj直接乘起来得到的)怎么转化到另一组基,使得表示的矩阵形式上全部由不可约表示组成;或者说,在群的意义下将表示矩阵分块对角化,$D=S\Lambda S^{-1}$,求这个S
那就将待求的不可约基$\ket{w^\lambda_{\alpha l}}$在张量基下展开
\[|w^\lambda_{\alpha l}>=\sum_{ij} |w_{ij}><w_{ij}|w^\lambda_{\alpha l}>\]其中$\braket{w_{ij}}{w^\lambda_{\alpha l}}$被称作CG系数,也可以写作$<i,j,(\mu,\nu),\alpha,\lambda,l>$
换基后矩阵元的变化
\[D^\mu(g)^{i'}_iD^\nu(g)^{j'}_j=<i'j'|\alpha\lambda l'>D^\lambda(g)^{l'}_l<\alpha\lambda l|ij>\]代入矩阵元的正交归一和完备性定理,同样有CG系数的正交归一和完备性定理,我就不再抄了
群代数、表示、左模
虽然上课没讲,但是这些东西还是知道一下比较好
群表示:G是一个群,V是域K上的一个线性空间,则G到V上全体可逆线性变换构成的群GL(V)的一个群同态φ称为群G在域K上的一个线性表示,简称为表示,称V为表示空间。若V为有限维,则称$dim_KV$为表示的次数或维数,记作$deg\varphi$
表示可以由二元组记作$(\varphi,V)$(群同态,表示空间)
群代数:(在群上赋予类似模或者线性空间的加法结构)K[G]是域K上的线性空间,在K[G]中定义如下乘法运算
\[(\sum_{g\in G}a_gg)(\sum_{h\in G}b_hh):=\sum_{g\in G}\sum_{h\in G}(a_gb_h)\]则K[G]成为群G在环K上的群环;K[G]也成为群G在域K上的群代数
设$(\varphi^*,V)$是群代数K[G]的一个线性表示,定义K[G]对V的乘法
\[av:=\varphi^*(a)(v)~~,~\forall a\in K[G],v\in V\]该运算满足
\[a(v+u)=av+au\] \[(a+b)v=av+bv\] \[(ab)v=a(bv)\] \[1v=v\] \[a(kv)=k(av)=(ka)v\]所以V成为K[G]上的一个左模
感觉就是群元同时承担两个作用:矢量(空间基)和变换(作用)
群代数的中心:
\[Z_{kG}=\{z\in kG|xz=zx,\forall x\in kG\}=\{z \in kG|gzg^{-1}=z,\forall g\in G\}\]还是描述的与全体的可交换性。但是与群中心相比,此处的对象范围更广了,允许出现多个群元线性组合的形式。比如我取一个共轭类i,把里面的元素全部求和形成一个群代数上的元素xi,这个xi一定是在群代数中心的。
群代数中心的结构:
设群G中的共轭类用i表示,令$z_i=\sum_{g\in class~i}g$,则
\[Z_{kG}=\bigoplus k_i z^i\]看见“共轭类数=不等价不可约表示数”这个证明可以用“类和向量构成群代数中心的基”,但是前置东西超出我的能力范围看不懂了。。哭
理想速复习:(吸收性)任意环元r作用在加法子群I上,rI一定在I的里面
模速复习:把线性空间的数域改成环
模的子模:空间的不变子空间;表示的分解:模分解成子模的直和
单模(或不可约模):没有非平凡子模的模,定位与不可约表示同级
幂等元:$e_\mu e_\nu=\delta_{\mu\nu}e_\mu$(这是物理群论书上的定义,比数学书多要求了正交性)
本原幂等元:生成最小左理想的幂等元
本原幂等元的充要判定:$e_ire_i=\lambda_re_i,\forall r\in K[G]$
本原幂等元与不可约表示:两个本原幂等元生成等价不可约表示当且仅当存在群代数中的元素r,使得$e_1re_2!=0$
幂等元与不可分解理想:环A的幂等元e本原当且仅当A的左理想Ae不可分;环A的中心幂等元e本原当且仅当A的双边理想Ae不可分;环的两个本原中心幂等元正交或相等
群代数的不可分左理想对应一个不可约表示:选取最小左理想中的基矢,用群元左作用在每个基矢上,生成一个矩阵(线性变换)
一些粗略的思考(不一定对):幂等元可以对代数结构进行划分(投影之类的)(且有很好的正交完备性,求和为1)Ae直接坍缩(简并)成一个左理想了,本原幂等元的划分是单的(不可再分性)
一个共轭类对应群代数中心的一个基矢;群代数中心还可以由幂等元张成(直和Ae),后者代表着不可约表示(个数)
杨图杨表
本质上在做一个整数拆分。杨图用从上到下不严格递减的总数为n的小方块描述了n的一种拆分(组合数学里的东西,懒得抄了)
对于Sn,n的拆分方案数=杨图数=共轭类数=不等价不可约表示数(因为Sn的共轭类与循环节规格完全挂钩,在本文1-3已证)
杨表:对于一个有n个格格的杨图,把1~n这几个数字填入框框中,就得到了杨表
normal杨表:填数字的顺序完全固定,(就跟大多数人写字一样)从上到下从左到右依次递增填1~n;normal杨表通过Sn置换可以变为其他的普通杨表
standard杨表:填数字顺序半固定:每行从左往右递增,每列从上到下递增即可
现在在杨表中作用Sn;如果置换保行(只水平动),那就叫对称子(Symmetrizer);保列就叫反对称子(Anti-symmetrizer)。
对于一个杨图(易得唯一的normal杨表),我们可以分别写出这两个向量(本节中,向量常常代表群代数中的元素)
\[s=\sum h~~;~~a=\sum(-1)^vv\]s代表把保行的所有置换加起来,a表示把保列的所有置换(奇置换要乘-1)加起来
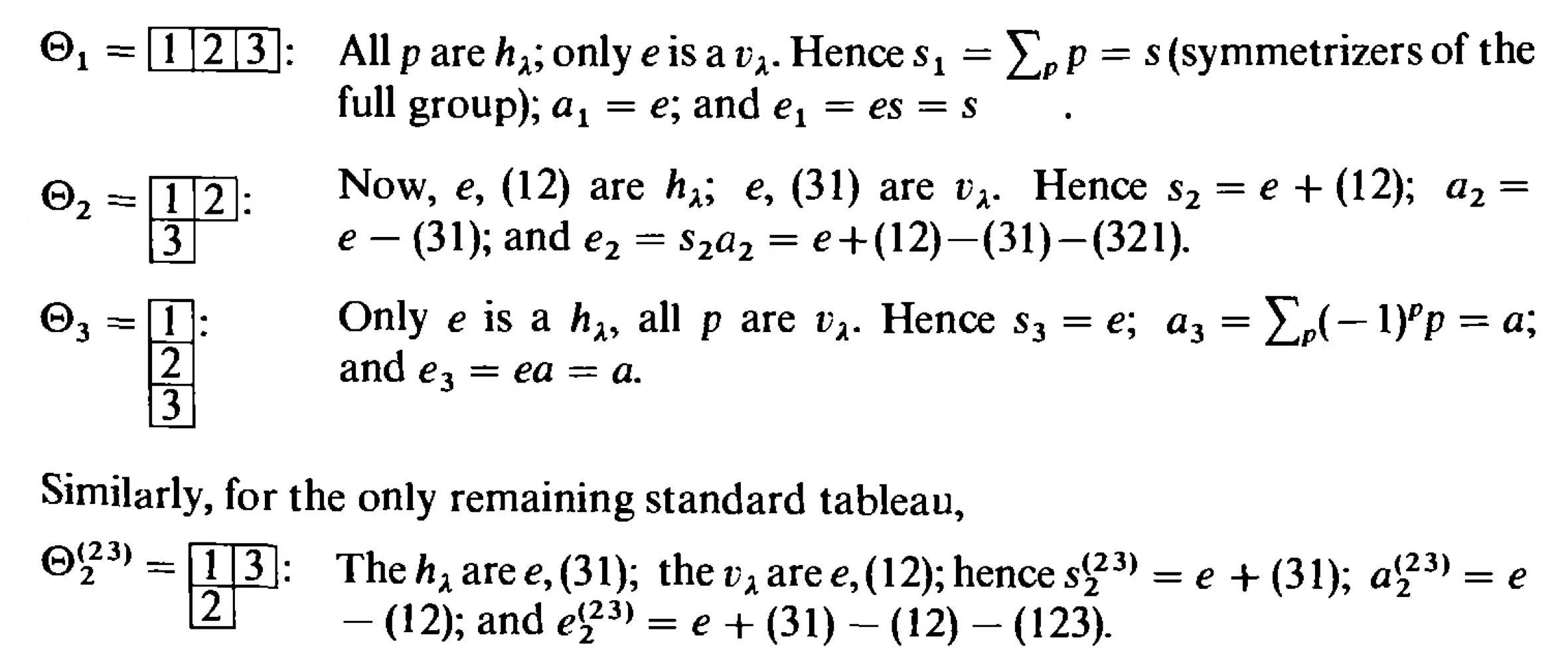
最后把sa乘起来得到向量e(由于一个是横向置换,一个是纵向置换,所以sa=as)
性质:
1.注意到s和a包含了对每行(列)置换完整的求和,所以任取一个行置换作用在s的左右(或者列置换作用在a的左右),(由于重排引理)其结果仍然是s(或者a)本身
进一步地,s和a都是群代数中的幂等元(但是非本原),s与a的乘积e是本原幂等元。
利用杨图生成Sn的不可约表示:
杨图对应整数划分-对应循环节格式-对应某个共轭类-(1:1)-不等价不可约表示数
杨图所对应的standard杨表数-表示维度-利用钩子定理计数:
standard杨表数为
\[\frac{n!}{\Pi hook(i)}\]i代表某个格子,hook(i)代表从这个格子的右手边最右端开始走,一直往左走走到i这个格子,再往下一直走出去,路过的格子数就是hook(i);然后你再把每个格子的钩子数乘起来放在分母就可以算表示维度了
对于每个杨图你可以通过乘sa的方式得到一个本原幂等元e,这玩意就是最小左理想的一个基;当表示维度>1时,很显然你还得找左理想中其他的基;方法就是用群元不断作用在e上就好了,最后达到的效果是用维度个矢量表示这一整个理想,每个群元在基矢上的作用并作一个矩阵
性质(示意):
横着排一行的杨图对应的e是将所有置换求和,该e在群作用下不变,所以是平凡表示
竖着排一列的杨图对应的e是将所有置换按符号交错求和,区分且仅区分出了置换的奇偶性,对应着Sn/An=C2的那个1-1…一维表示
一些胡思乱想:每个不可约表示都是群的某些特性被忽略,选中一个特性进行体现的结果(模掉了什么东西。。),对应着幂等元的投影。而在杨图中(由于群代数加法的可交换性),加号相连的置换之间的某些差别被模掉了,所以就生成了极小左理想,就是不可约表示
撒谎理论
从这里进入光滑拓扑群部分了,冲冲冲
连续群在单位元附近做展开,一阶导就是生成元
\[D(d_\alpha)=I-id_{\alpha_a}X_a+...\]则$X_a$为生成元
\[X_a=i\frac{\partial}{\partial\alpha_a}D(\alpha)|_{\alpha=0}\]是的,你没看错,前面两个式子里的i就是虚数单位,而不是什么id恒等映射(我之前就看错了),据说是物批为了计算方便提出来的一个系数(联想到虚宗量贝塞尔函数),有些人会提-i,数批也许不会提这个,但是本质上不会改变什么
另一个值得注意又比较显然的一点,李群独立参数个数=李代数维度=李代数生成元个数
利用无穷小变换连续乘积的形式把任一群元展开
\[D(\alpha)=(I-i\frac{\alpha_a}{N}X_a)(I-i\frac{\alpha_a}{N}X_a)...(I-i\frac{\alpha_a}{N}X_a)~~;N\to\infty\] \[D(\alpha)=(I-i\frac{\alpha_a}{N}X_a)^N~~~;N\to\infty\]这个在形式上和指数函数expx的极限定义,所以利用e指数的形式记作
\[D(\alpha)=e^{-iX_a\alpha_a}\]注:这只是一种记法,事实上流形上的指数映射和狭义的指数函数有很多可以类比的地方,但是把所有性质完全等同起来是不可取的(在下面我们将看到,交换性的加法群上的指数函数实际上是这个东西的一个截断)
至此,我们用指数形式建立了群元(李群)与无穷小变换(李代数)之间的对应关系。在上面的关系式中,D(α)是李群中的元素,$X_a$是李代数中的元素
下面抄一下代数的定义:
设K是一个域,R是一个环,如果满足:
1.(R,+)构成域K上的向量空间
2.(ka)b=k(ab)=a(kb),$\forall k \in K,a,b\in R$
则称R是域K上的一个代数或K-代数,向量空间R的维数称为代数R的维数,环R的单位元成为代数R的单位元
简单的来看一下,大概就是配备了环乘法的线性空间。注意:在物批研究的大多数李代数中,此处的环乘法即为对易算符[A,B]=AB-BA,后者由矩阵乘法定义
李代数的定义:(from参考4,按照一般习惯微调)
域F上的线性空间L,配备乘法运算$L\times L\to L$,记作[x,y],叫做x与y之间的对易子或者李括号,满足下面这三条就叫做F上的李代数
1.李括号双边线性
2.[x,x]=0 for all x in L
3.[x,[y,z]]+[y,[z,x]]+[z,[x,y]]=0 (Jacobi恒等式)
CBH公式
全称campbell-baker-Hausdorff公式(也有说法是BCH公式,人名换位),描述了李代数乘法法则与李群乘法法则之间的对应关系
若有
\[e^Ae^B=e^C\]其中,ABC在李代数中,e^A等在李群中,则有关系式
\[C=A+B+\frac{1}{2}[A,B]+\frac{1}{12}([A,[A,B]]+[[A,B],B])+...\]更具体的(在知乎上抄的,这谁知道对不对啊)(from参考3)
\[C=\sum_{n=1}^\infty \frac{(-1)^{n-1}}{n}\sum_{r_i+s_i>0}\frac{1}{\sum_{i=1}^n(r_i+s_i)\Pi_{i=1}^nr_i!s_i!}[A^{(r_i)},B^{(s_1)},...,A^{(s_n)},B^{(s_n)}]\]其中$A^{(r_j)}$代表A连续出现j次
\[[X_1,X_2,..,X_m]=[X_1,[X_2,[...,[X_{m-1},X_m]...]]]\]证明CBH公式:(抄自参考5)
引理:
\[e^ABe^{-A}=B+[A,B]+\frac{1}{2}[A,[A,B]]+...+\frac{1}{n!}[A,[A,...[A,B]...]]+..\]通项中,$\frac{1}{n!}$后对应着A出现n次,B出现一次
引理证明:
设算符F->End(V)(就是进去一个标量出来一个矩阵)(标量乘矩阵定义为把矩阵所有分量都乘一下这个标量,所以x与A对易)
\[U(x)=e^{xA}Be^{-xA}\]注意到(第二个等号是因为A与expxA对易)
\[\frac{d}{dx}U(x)=e^{xA}ABe^{-xA}-e^{xA}Be^{-xA}A \\=A(e^{xA}Be^{-xA})-(e^{xA}Be^{-xA})A=[A,U(x)]\]对上式两端dx积分得
\[U(x)=U(0)+\int_0^x[A,U(t)]dt=B+\int_0^x[A,U(t)]dt\]这个积分方程可以通过逐项逼近的方法来求级数解(就是算下一个更精确解时,右边积分中U代入上一个解)来算几个试试
令$U_0(x)=0$,则
\[U_1(x)=B+\int_0^x[A,0]dt=B\] \[U_2(x)=B+\int_0^x[A,B]dt=B+[A,B]x\] \[U_3(x)=B+\int_0^x[A,B+[A,B]t]dt\\ =B+\int_0^x[A,B]dt+\int_0^x[A,[A,B]]tdt=B+[A,B]x+\frac{1}{2}[A,[A,B]]x^2\] \[...\]设$U_l(x)=\sum_{i=0}^l\frac{1}{i!}[A^{(i)},B]x^i$,迭代下一个
\[U_{l+1}(x)=B+\sum_{i=0}^l\frac{1}{i!}\int_0^x[A,[A^{(i)},B]]x^idt\\ =B+\sum_{i=0}^l\frac{1}{(i+1)!}[A,[A^{(i)},B]]x^{i+1}=\sum_{i=0}^{l+1}\frac{1}{i!}[A^{(i)},B]x^i\]所以原积分方程的解是(咳、其实敛散性没讨论(x))
\[U(x)=e^{xA}Be^{-xA}=\sum_{i=0}^\infty\frac{1}{i!}[A^{(i)},B]x^i\]令x=1,引理得证 口
该引理的推论:
\[e^{-xB}Ae^{xB}=\sum_{i=0}^\infty\frac{1}{i!}[A,B^{(i)}]'x^i~~~(1)\]↑注意这个式子多重李括号的中心在最左边!所有括号都把A括住的那种
\[e^{-A(x)}\frac{d}{dx}e^{A(x)}=e^{-A}A'e^A=\sum_{i=1}^\infty\frac{1}{i!}[A',A^{(i-1)}]~~~(2)\]设
\[e^{G(x)}=e^{xA}e^{xB}\] \[G(x)=\sum_{i=1}^\infty x^iG_i\](定义式代入x=0可以看出G(0)=0,所以G没有常数项,求和从1开始);证明的主要目的就是求出每一项系数Gi
定义式求导并右乘自身逆得
\[e^{-xB}e^{-xA}\frac{d}{dx}e^{xA}e^{xB}=e^{-G(x)}\frac{d}{dx}e^{G(x)}\]分成左右两部分计算(第二个等号代入了推论1式)
\[LHS=e^{-xB}Ae^{xB}+B=B+\sum_{i=0}^\infty\frac{1}{i!}[A,B^{(i)}]'x^i\]右边代入推论2式
\[RHS=\sum_{i=1}^\infty\frac{1}{i!}[G',G^{(i-1)}]\]需要计算多项式G与导数之间的多重李括号时,利用无穷级数展开计算
\[G(x)=\sum_{i=1}^\infty x^iG_i~~~;~~~G'(x)=\sum_{i=1}^\infty i x^{i-1}G_i\]利用李括号的双边线性性
\[[G',G]=[\sum_{i=1}^\infty i x^{i-1}G_i,\sum_{i=1}^\infty x^iG_i]=x^2[G_1,G_2]+2x^2[G_2,G_1]+O(x^3)\\ =-x^2[G_1,G_2]+O(x^3)\]理论上每一项都是可以算出来的,只是通项比较复杂(组合性很强,一开头也摆出来了),就只算前几项为例;代入RHS展开式中
\[RHS=G_1+2xG_2+x^2(3G_3-\frac{1}{2}[G_1,G_2])+O(x^3)\]现在就可以和LHS的级数结果比较系数解出G_i了
\[G_1=A+B\] \[G_2=\frac{1}{2}[A,B]\] \[G_3=\frac{1}{12}([A,[A,B]]+[B,[B,A]])\]故
\[e^Ae^B=e^{A+B+\frac{1}{2}[A,B]+\frac{1}{12}([A,[A,B]]+[B,[B,A]])+...}\]想要多少项就算多少项,证毕
对易括号就是李代数中的乘法,也就是说,当李代数中的运算唯一确定时,李群中的乘法表也被唯一确定了;和所有线性空间一样,确定维度个基矢(李代数生成元)之间的乘法表后,全体的乘法关系也就被确定了。可以看出,CBH公式中有大量的连环李括号,我想这就是为什么GTM9一直在研究什么半单啊可解啊的原因吧
取李代数上的两个生成元$X_a$、$X_b$,做对易括号后得到的结果仍是李代数中的一个矢量,将这个矢量在确定的生成元下展开,写作
\[[X_a,X_b]=if_{abc}X_c\]等式右侧使用了求和约定,也就是说,$if_{abc}$是生成元ab对易子在生成元c下的展开系数,fabc叫做结构常数(当时还吐槽这玩意很像克氏符啥的233)
由于对易括号的反对称性,结构常数也具有反对称性;由于括号满足Jacobi恒等式,相应的结构常数也满足
\[if_{ade}if_{bcd}+if_{bde}if_{cad}+if_{cde}if_{abd}=0\]SO(2)
这一套我在李丽里干过的来着
SO(2)群是平面转动群,矩阵上是正交且det=1的2x2矩阵由矩阵乘法组成的群
SO2群是单参控制的(一维),可以写作
\[R(\phi)=\begin{pmatrix} cos\phi&-sin\phi\\ sin\phi&cos\phi \end{pmatrix}\]几何性质:注意到$R(\phi)=R(\phi+2k\pi),k\in Z$,所以$R(\phi)\cong\mathbb{R}/2\pi$,也就是个圆弧
生成元:
利用公式
\[R(d\phi)\approx I-i(d\phi)X,d\phi\to 0\]其中X是生成元
\(R(d\phi)=\begin{pmatrix} cosd\phi&-sind\phi\\ sind\phi&cosd\phi \end{pmatrix}\approx \begin{pmatrix} 1&-d\phi\\ d\phi&1 \end{pmatrix}=I-i\begin{pmatrix} 0&-i\\ i&0 \end{pmatrix}d\phi\) 则
\[J=\begin{pmatrix} 0&-i\\ i&0 \end{pmatrix}\]是SO(2)的生成元;对应的李代数so(2)由所有2x2实反对称矩阵(单参控制)构成
将生成元J代入$R(\phi)=e^{-iJ\phi}$,注意到$J^2=-I$(J这东西本来就对标虚数单位)
\[R(\phi)=e^{-iJ\phi}=I-iJ\phi-\frac{1}{2}J^2\phi^2+\frac{1}{6}iJ^3\phi^3+...\\ =I(1-\frac{1}{2}\phi^2+...)+iJ(\phi-\frac{1}{6}\phi^3+...)\\ =Icos\phi+iJsin\phi=\begin{pmatrix} cos\phi&-sin\phi\\ sin\phi&cos\phi \end{pmatrix}\]SO(3)
三维转动群,由于先前的(李丽?)知识我们已经知道这玩意有3维(所以只有三维里才有叉乘,伟大!)
也即,3x3实正交矩阵,且det=1
几何性质:
欲表达一个三维转动,你需要两个角度参数描述一个轴,加上一个参数描述转过多少角度
轴$\hat n(\theta,\phi),\theta\in[0,\pi],\phi\in[0,2\pi)$,角度$\psi\in[0,\pi]$
因为$R_{\hat n}(\psi)=R_{-\hat n}(2\pi-\psi)$,所以上面确定范围的时候涉及到一次兼并
可以建立以ψ为长度,$\hat n$为方向的向量,则SO(3)几乎与3维半径为Π的实心球一一对应,除了表面上相对的两个点代表SO(3)中同一元素。($R_{\hat n}(\pi)=R_{-\hat n}(\pi)$)
\[SO(3)\sim \mathbb{R}P_3\]后者的一维同调群非平凡,故SO(3)是双连通区域;在SO(3)球中做一条闭合曲线,有一类(不跨最外层)可以连续变换到一个点上;而有一类(利用对径相同的性质跨越最外层)不可以连续变换到一个点上
内层逻辑是因为“闭合”借用的是转动的实际意义,而“连续”仅仅在流行上看,跳过外表面不能算作连续
SO(3)下的不变张量:
二阶不变张量:$\delta_{ij}$
\[R_k^iR_l^j\delta^{kl}=\delta^{ij}\]这是由转动的正交性保证的
三阶不变张量:$\varepsilon^{lmn}$
\[R_l^iR_m^jR_n^k\varepsilon^{lmn}=\varepsilon^{ijk}\]这是由det=1及行列式的反对称性保证的,特殊地,$det(R)=R_l^1R_m^2R_n^3\varepsilon^{lmn}=1$
三维转动的欧拉角描述
这个在李丽里也有写,懒得再写一遍了,就写一下角度取值范围吧:两边转角在[0,2pi),中间转角在[0,pi];且大多数量力、群论教材对中间那一次旋转的定义是绕y轴的
SO(3)生成元
和寻找SO(2)生成元的步骤类似,首先写出绕xyz轴旋转的矩阵,再求导或者一阶小量展开
绕x旋转
\[\begin{pmatrix} 1&&\\ &cos\theta&-sin\theta\\ &sin\theta&cos\theta \end{pmatrix}\]对其取一阶θ->0
\[\begin{pmatrix} 1&&\\ &1&-\theta\\ &-\theta&1 \end{pmatrix}\]故生成元
\[J_1=\begin{pmatrix} &&\\ &&-i\\ &i& \end{pmatrix}\]这里就可以看出提出系数i的原因,正是让生成元矩阵厄米
同理可得绕y与绕z的生成元
\[J_2=\begin{pmatrix} &&i\\ &&\\ -i&& \end{pmatrix}\] \[J_3=\begin{pmatrix} &-i&\\ i&&\\ && \end{pmatrix}\]可以看出对应的李代数so(3)由3x3反对称矩阵组成(好吧,数批说是实反对称,物批提了个i之后说这是纯虚矩阵,同时也是厄米阵)
生成元的Levi-Civita符号表示
\[(J_k)^l_{~m}=-i\varepsilon_{klm}\]由此可以算得,三个方向上生成元的平方和
\[J^2=J_1^2+J_2^2+J_3^2=\begin{pmatrix} &-1&-1\\ -1&&-1\\ -1&-1& \end{pmatrix}\]对SO(3)中共轭类的刻画
先上结论:所有转动同一角度(轴可以不同)的转动元在同一共轭类(并且一个共轭类就是仅由这些东西组成的)
我喜欢这个结论,很漂亮也很好理解

看这个芙芙,一种是她(绕着自己为轴)转动了φ;另一种是她先倒下来,转动一个φ,再站回去,当然两个效果是一样的啦~
证明:仅需证明{绕n1轴转动φ}效果完全等同于{任意一次空间旋转D:将n1转到n2}->{在转动后的空间绕n2旋转φ}->{执行D逆:将n2转回n1}(后面的三个操作从左往右读)
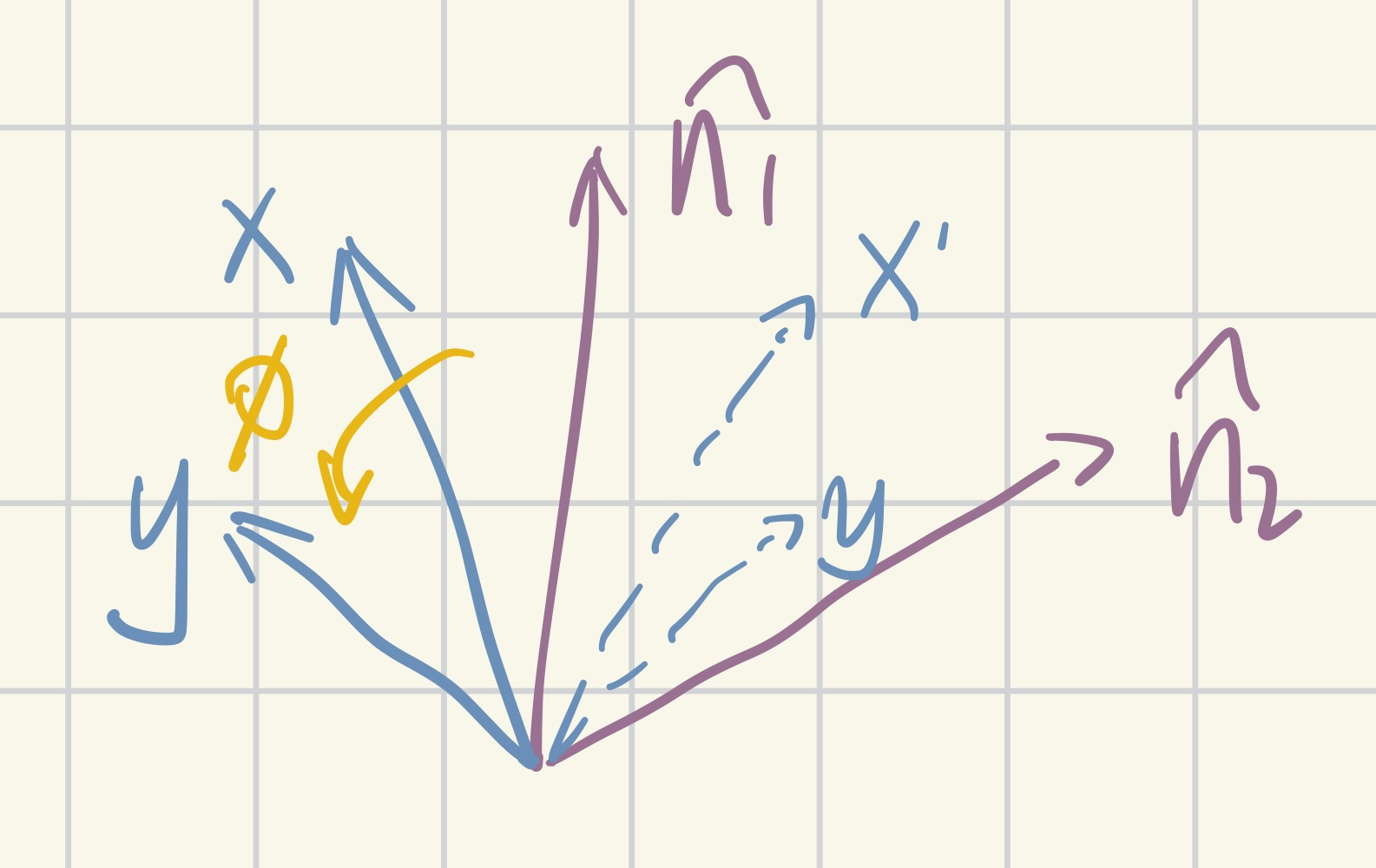
此定理为自证明,请自行甄别可行性(好啰嗦)
绕n1将x向量旋转φ角,可得y向量,此时n1、x、y三个向量之间的夹角是确定的(相对位置确定),且y与x、n1之间的夹角只由{x与n1之间的夹角}和{转角φ}两者决定
现在对全空间施以一个旋转操作D,记n1旋转之后的位置为n2,x旋转至x’,y旋转至y’,下证x’绕n2旋转φ后恰落在y’的位置:
因为D是旋转操作,有保内积性=>保角性,即n2,x’,y’三者之间的夹角不变.
由于一次绕轴转动后,所产生的新向量与{原向量}和{轴}之间的夹角仅由{原向量和轴之间的夹角}和{转角}决定;在执行D变换的前后,进行绕轴旋转φ时,{x与n1之间的夹角}={x’与n2之间的夹角},所以x’绕n2旋转φ后得到的向量与x’、n2之间的夹角分别等于y’与x’、n2之间的夹角
两个(含手性的)夹角恰能唯一决定一个方向,长度始终=x,所以x’绕n2旋转φ后恰落在y’的位置,可以视作x’绕n2旋转φ后为y’。
现在执行逆变换$D^{-1}$,它一定会将y’变换到y的位置上,也即{绕n1轴转动φ}效果完全等同于{任意一次空间旋转D:将n1转到n2}->{在转动后的空间绕n2旋转φ}->{执行D逆:将n2转回n1},证毕
绕任意轴的旋转
有了这个结论之后,就可以将欧拉角的非定轴转动改为三个定轴转动了
设xyz轴分别标号123,不带’表示定轴,带’表示转动后的坐标轴,下面对欧拉角的表达式进行化简
\[R_{3'}(\gamma)R_{2'}(\beta)R_3(\alpha)=R_{2'}(\beta)R_3(\gamma)R_{2'}^{-1}(\beta)R_{2'}(\beta)R_3(\alpha)\\ =R_{2'}(\beta)R_3(\gamma)R_3(\alpha)=R_3(\alpha)R_2(\beta)R_3^{-1}(\alpha)R_3(\gamma)R_3(\alpha)\\ =R_3(\alpha)R_2(\beta)R_3(\gamma)\]也即,欧拉角转动效果等价于绕定轴逆序旋转原有角度。
将注意力放在绕定轴n转动任意角度,这构成了SO(3)的一个正规子群,且同构于SO(2),是单参Lie群,必定对应着单个生成元$J_n$
我们已经知道了对一个定轴转动$R_n(\phi)$,左右包一个特定转动,就可以得到想要的绕a转动$R_a(\phi)$,那么生成元呢?是不是也可以通过左右包转动的操作来得到想要的轴生成元呢?
(定理0)答案是肯定的,利用泰勒展开作为桥梁,计算一下(在高次项中补足一些$D^{-1}D$即可)
\[DR_{n_1}(\phi)D^{-1}=De^{-iJ_{n_1}\phi}D^{-1}=D(1-iJ_{n_1}\phi-\frac{1}{2}J_{n_1}^2\phi^2+...)D^{-1}\\ =1-iDJ_{n_1}D^{-1}\phi-\frac{1}{2}DJ_{n_1}D^{-1}DJ_{n_1}D^{-1}\phi^2+...\\ =e^{-iDJ_{n_1}D^{-1}\phi}\]也就是说,左右被同样的转动夹住,可以将其变为一个转动后的生成元J,下面有两条定理描述这个性质,以及J1,J2,J3类似于正交基矢的可以用来描述任意生成元的良好性质
因为这两条性质并列来看可以互相促进理解,所以我将定理及解释写在一起,之后再写证明、
1.$J_k$(k=1,2,3)在旋转下的操作类似于基矢{$e_k$}
\[RJ_kR^{-1}=J_lR^l_{~k}\]解释:我们现在随便拿一个旋转矩阵
\[R=\begin{pmatrix} r_{11}&r_{12}&r_{13}\\ r_{21}&r_{22}&r_{23}\\ r_{31}&r_{32}&r_{33} \end{pmatrix}\]回忆一下矩阵对于线性变换最朴素的理解方式:这个操作将第一个基矢转到第一个列向量,以此类推,也即它是由三个转动后的基矢列向量并成的。
并且不妨取k=3,等式右侧即为$r_{13}J_1+r_{23}J_2+r_{33}J_3$,若是把{Ji}看作线性空间中的一组基,则这正是旋转后的第三个基矢在旋转前基矢下的展开!这就是为什么说“在旋转下的操作类似于基矢{$e_k$}”
2.任一归一化后的向量$\hat n=(n^1,n^2,n^3)$,则在$\hat n$转动方向上的生成元$J_n$可以被基矢对应的生成元J1,J2,J3展开为
\[J_n=J_kn^k\]这条定理是说,J123发挥基矢作用,其效果于e123是并行的,可以看出任意轴对应的J具有很好的结构,可以被很容易地表示
1.证明:把之前关于ε不变的等式拿过来
\[R^i_lR^j_mR^k_n\varepsilon^{lmn}=\varepsilon^{ijk}\]左乘${R^T}^s_{~i}$,得
\[{R^T}^s_{~i}R^i_lR^j_mR^k_n\varepsilon^{lmn}={R^T}^s_{~i}\varepsilon^{ijk}\]利用$R^TR=I$的特性
\[R^j_m\varepsilon^{smn}(R^T)^n_k=\varepsilon^{ijk}{R}^i_{~s}\]反代入生成元的Levi-Civita符号表示
\[i(J_k)^l_{~m}=\varepsilon_{klm}\] \[R^j_m(J_s)^m_n(R^T)^n_k=(J_i)^j_k{R}^i_{~s}\]改为矩阵相乘形式(去掉分量)
\[RJ_sR^{-1}=J_i{R}^i_{~s}\]证毕
2.证明:设有转动R将z轴方向向量(0,0,1)转置$\hat n=(n^1,n^2,n^3)$,则该转动矩阵R的第三列向量必为$\hat n=(n^1,n^2,n^3)$,由定理0和1可得
\[J_n=RJ_3R^{-1}=J_kR^k_3=n^1J_1+n^2J_2+n^3J_3\]生成元的对易性、谱性质
超级大注明:本节能使用的工具有且仅有:$J_1$、$J_2$、$J_3$组成一个三元李代数,并且他们之间的李括号定义为
\[[J_k,J_l]=i\varepsilon_{klm}J^m\]所以请迅速丢掉上一章我们给出的生成元矩阵形式,现在能用的只有这个运算律。本节开始的目标为:寻找该李代数的表示,进而寻找SO(3)的表示
事实上先前的矩阵形式生成元也满足这个对易关系,但是下面我们应该设法寻找其他的表示
定义:$J_\pm$
\[J_\pm=J_1\pm iJ_2\]关于$J_\pm$的相关李括号
\[[J_3,J_\pm]=[J_3,J_1]\pm i[J_3,J_2]=iJ_2\pm i(-iJ_1)=iJ_2\pm J_1=\pm(J_1\pm iJ_2)=\pm J_\pm\] \[[J_+,J_-]=[J_1+iJ_2,J_1-iJ_2]=-i[J_1,J_2]+i[J_2,J_1]=-2i[J_1,J_2]=2J_3\]以及$J_\pm^\dagger=J_\mp$
在稍前面一点我们定义了$J^2$(总角动量平方算符=所有分量平方和),下面计算$J^2$与$J_k$(k=1,2,3)的李括号(就取k=1为例好了)
\[[J^2,J_1]=[J_2^2,J_1]+[J_3^2,J_1]=J_2(-iJ_3)+(-iJ_3)J_2+J_3(iJ_2)+(iJ_2)J_3=0\]tips:平方李括号公式(很易推)$[a^2,b]=a[a,b]+[a,b]a$
由轮换对称性可得$\forall k\in{1,2,3},[J^2,J_k]=0$,进一步的,有$[J^2,J_\pm]=0$
下面开始利用升降算符$J_\pm$进行特征(及特征空间)的升降,下文中不加说明时一般默认$\ket{\lambda,m}$是$J^2$下特征为$\lambda$的特征向量,也是是$J_3$下特征为m的特征向量
利用$[J_3,J_+]=J_+$,有
\[J_3J_+|m>=[J_3,J_+]|m>+J_+J_3|m>=J_+|m>+mJ_+|m>=(m+1)J_+|m>\]可见,$J_+$作用在$J_3$下特征为m的的特征向量后,会将其转到特征为m+1的特征空间内。
那么$J^2$的场合如何呢?来算算
\[J^2J_+|\lambda>=J_+J^2|\lambda>=\lambda J_+|\lambda>\]也即,上升下降算符不会改变总角动量的特征值
既然可以一直这么上升下降,那么我们就应当试图导出一种截断
定理(J3特征值的上界估计):总角动量平方$J^2$的特征值$\lambda$是3方向上生成元$J_3$特征值平方$m^2$的上界
证明:注意到$J^2-J_3^2=\frac{1}{2}(J_+J_-+J_-J_+)$,$J_\pm$互为共轭转置,利用这点作用在非零的$\ket{j,m}$上,有
\[\begin{aligned} & < \lambda,m|J^2-J_3^2|\lambda,m> \\ & = \frac{1}{2}<\lambda,m|J_+J_-+J_-J_+|\lambda,m> \\ & = \frac{1}{2}(<\lambda,m|J_-^\dagger J_-|\lambda,m>+<\lambda,m|J_+^\dagger J_+|\lambda,m>) \geq 0 \end{aligned}\]另一方面,直接将$J^2-J_3^2$作用在$\ket{\lambda,m}$上,可得
\[<\lambda,m|J^2-J_3^2|\lambda,m>=(\lambda-m^2)<\lambda,m|\lambda,m>\]
由于模方为正,故有
\[\lambda-m^2\geq 0\]也即,无论上升还是下降,$m^2$均不能超过$\lambda$,设$min~m=j’~;~max~m=j$,则用上升算符作用在最大特征值的特征向量上,必然为0向量
\[0=J_-J_+|\lambda,j>=(J^2-J_3^2-J_3)|\lambda,j>=(\lambda-j^2-j)|\lambda,j>\]则$\lambda=j(j+1)$;同理让$J_+J_-$作用在最小特征j’上,可得等式$\lambda=j’(j’-1)$,故
\[j(j+1)=j'(j'-1)\]解得j’=j+1(舍)或-j,即j’=-j,$\lambda=j(j+1)$,以后可以直接用$\ket{j,m}$来表示一个特征向量了,不过注意J^2对应的特征向量是j(j+1)
下面计算上升下降算符对向量模长产生的影响,设 \(J_+|j,m>=a_{im}|j,m+1>~;~J_-|j,m>=b_{jm}\) ,则 \(|a_{jm}^2|<j,m+1|j,m+1>=<j,m+1|J_-J_+|j,m+1>\\ =(j(j+1)-m^2-m)<j,m|j,m>\) 故 \(|a_{jm}|=\sqrt{j(j+1)-m(m+1)}=\sqrt{(j-m)(j+m+1)}\) 同理 \(|b_{jm}|=\sqrt{(j+m)(j-m+1)}\)
本篇到此结束,下一篇https://zhuanlan.zhihu.com/p/692020167
参考资料
1.董无极《Group Theory in Physics》
2.丘维生《群表示论》
3.https://zhuanlan.zhihu.com/p/618624483
4.GTM9
5.http://webhome.phy.duke.edu/~mehen/760/ProblemSets/BCH.pdf
原创文章转载请注明出处: 群论一
